
题目列表(包括答案和解析)
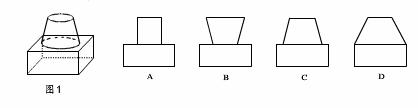
3.如图1是一个几何休的实物图,则其主视图是
2.我国第六欢人口普查的结果表明,目前肇庆市的人口约为4050000人,这个数用科学记教法表示为
A.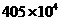 B.
B.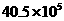 C.
C.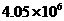 D.
D.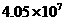
1.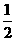 的倒数是
的倒数是
A.2 B. 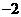 C.
C.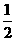 D.
D.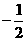
28、(2011•南京)[问题情境]
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
[数学模型]
 设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+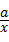 )(x>0).
)(x>0).
[探索研究]
(1)我们可以借鉴以前研究函数的经验,先探索函数y=x+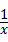 (x>0)的图象和性质.
(x>0)的图象和性质.
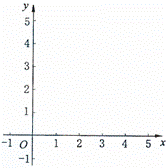
①填写下表,画出函数的图象;
|
x |
… |
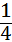 |
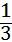 |
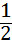 |
1 |
2 |
3 |
4 |
… |
|
y |
… |
|
|
|
|
|
|
|
… |
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数y=x+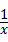 (x>0)的最小值.
(x>0)的最小值.
[解决问题]
(2)用上述方法解决“问题情境”中的问题,直接写出答案.
考点:反比例函数的性质;完全平方公式;配方法的应用;一次函数的性质;二次函数的最值。
专题:计算题。
分析:(1)①把x的值代入解析式计算即可;②根据图象所反映的特点写出即可;③根据完全平方公式(a+b)2=a2+2ab+b2,进行配方即可得到最小值;
(2)根据完全平方公式(a+b)2=a2+2ab+b2,进行配方得到y=2[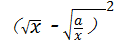 +2
+2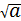 ],即可求出答案.
],即可求出答案.
解答:解:(1)①故答案为: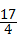 ,
,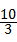 ,
,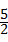 ,2,
,2,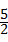 ,
,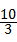 ,
,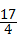 .
.
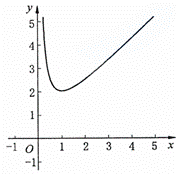
函数y=x+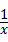 的图象如图:
的图象如图:
②答:函数两条不同类型的性质是:当0<x<1时,y 随x的增大而减小,当x>1时,y 随x的增大而增大;当x=1时,函数y=x+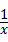 (x>0)的最小值是1.
(x>0)的最小值是1.
③解:y=x+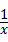 =
=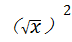 +
+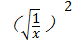 ﹣2
﹣2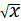 •
•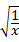 +2
+2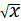 •
•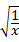 ,
,
=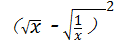 +2,
+2,
当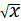 ﹣
﹣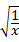 =0,即x=1时,函数y=x+
=0,即x=1时,函数y=x+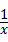 (x>0)的最小值是2,
(x>0)的最小值是2,
答:函数y=x+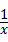 (x>0)的最小值是2.
(x>0)的最小值是2.
(2)答:矩形的面积为a(a为常数,a>0),当该矩形的长为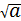 时,它的周长最小,最小值是4
时,它的周长最小,最小值是4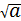 .
.
点评:本题主要考查对完全平方公式,反比例函数的性质,二次函数的最值,配方法的应用,一次函数的性质等知识点的理解和掌握,能熟练地运用学过的性质进行计算是解此题的关键.
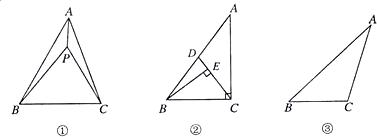
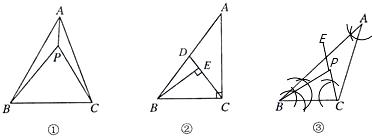
27、(2011•南京)如图①,P为△ABC内一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.
(1)如图②,已知Rt△ABC中,∠ACB=90°,∠ABC>∠A,CD是AB上的中线,过点B作BE丄CD,垂足为E.试说明E是△ABC的自相似点;
(2)在△ABC中,∠A<∠B<∠C.
①如图③,利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹);
②若△ABC的内心P是该三角形的自相似点,求该三角形三个内角的度数.
考点:相似三角形的判定与性质;直角三角形斜边上的中线;三角形的内切圆与内心;作图-复杂作图。
专题:作图题;几何综合题。
分析:(1)根据已知条件得出∠BEC=∠ACB,以及∠BCE=∠ABC,得出△BCE∽△ACB,即可得出结论;
(2)①根据做一角等于已知角即可得出△ABC的自相似点;
②根据∠PBC=∠A,∠BCP=∠ABC=∠2∠PBC=2∠A,∠ACB=2∠BCP=4∠A,即可得出各内角的度数.
解答:解:(1)在Rt△ABC中,∠ACB=90°,CD是AB上的中线,
∴CD=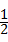 AB,
AB,
∴CD=BD,
∴∠BCE=∠ABC,
∵BE⊥CD,∴∠BEC=90°,
∴∠BEC=∠ACB,
∴△BCE∽△ACB,
∴E是△ABC的自相似点;
(2)①如图所示,
做法:①在∠ABC内,作∠CBD=∠A,;
②在∠ACB内,作∠BCE=∠ABC,BD交CE于点P,
则P为△ABC的自相似点;
②∵P是△ABC的内心,
∴∠PBC=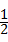 ∠ABC,∠PCB=
∠ABC,∠PCB=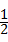 ∠ACB,
∠ACB,
∵∠PBC=∠A,∠BCP=∠ABC=∠2∠PBC=2∠A,∠ACB=2∠BCP=4∠A,
∴∠A+2∠A+4∠A=180°,
∴∠A=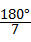 ,
,
∴该三角形三个内角度数为: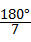 ,
,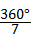 ,
,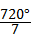 .
.
点评:此题主要考查了相似三角形的判定以及三角形的内心做法和做一角等于已知角,此题综合性较强,注意从已知分析获取正确的信息是解决问题的关键.
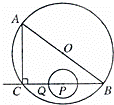
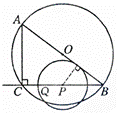
26、(2011•南京)如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
(1)当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
(2)已知⊙O为△ABC的外接圆.若⊙P与⊙O相切,求t的值.
考点:圆与圆的位置关系;勾股定理;直线与圆的位置关系;相似三角形的判定与性质。
专题:几何综合题;动点型。
分析:(1)根据已知求出AB=10cm,进而得出△PBD∽△ABC,利用相似三角形的性质得出圆心P到直线AB的距离等于⊙P的半径,即可得出直线AB与⊙P相切;
(2)根据BO=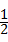 AB=5cm,得出⊙P与⊙O只能内切,进而求出⊙P与⊙O相切时,t的值.
AB=5cm,得出⊙P与⊙O只能内切,进而求出⊙P与⊙O相切时,t的值.
解答:解:(1)直线AB与⊙P相切,
如图,过P作PD⊥AB,垂足为D,
在Rt△ABC中,∠ACB=90°,
∵AB=6cm,BC=8cm,
∴AB=10cm,
∵P为BC中点,
∴PB=4cm,
∵∠PDB=∠ACB=90°,
∠PBD=∠ABC,
∴△PBD∽△ABC,
∴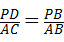 ,
,
即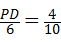 ,
,
∴PD=2.4(cm),
当t=1.2时,PQ=2t=2.4(cm),
∴PD=PQ,即圆心P到直线AB的距离等于⊙P的半径,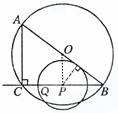
∴直线AB与⊙P相切;
(2)∵∠ACB=90°,
∴AB为△ABC的外接圆的直径,
∴BO=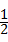 AB=5cm,
AB=5cm,
连接OP,
∵P为BC中点,∴PO=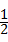 AC=3cm,
AC=3cm,
∵点P在⊙O内部,∴⊙P与⊙O只能内切,
∴5﹣2t=3,或2t﹣5=3,
∴t=1或4,
∴⊙P与⊙O相切时,t的值为1或4.
点评:此题主要考查了相似三角形的性质与判定以及直线与圆的位置关系和圆与圆的位置关系,正确判定直线与圆的位置关系是重点知识同学们应重点复习.
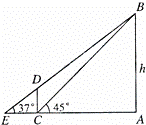
25、(2011•南京)如图,某数学课外活动小组测量电视塔AB的高度.他们借助一个高度为30m的建筑物CD进行测量,在点C处测得塔顶B的仰角为45°,在点E处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
考点:解直角三角形的应用-仰角俯角问题。
分析:在Rt△ECD中,根据三角函数即可求得EC,然后在Rt△BAE中,根据三角函数即可求得电视塔的高.
解答:解:在Rt△ECD中,tan∠DEC=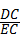 ,
,
∴EC=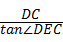 ≈
≈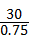 =40(m),
=40(m),
在Rt△BAE中,tan∠BEA=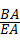 ,
,
∴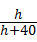 =0.75,
=0.75,
∴h=120(m),
答:电视塔的高度约为120m.
点评:本题主要考查了仰角俯角的定义,正确理解三角函数的定义是解决本题的关键.
24、(2011•南京)已知函数y=mx2﹣6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
考点:抛物线与x轴的交点;一次函数图象上点的坐标特征;二次函数图象上点的坐标特征。
专题:计算题。
分析:(1)根据解析式可知,当x=0时,与m值无关,故可知不论m为何值,函数y=mx2﹣6x+1的图象都经过y轴上一个定点(0,1).
(2)应分两种情况讨论:①当函数为一次函数时,与x轴有一个交点;
②当函数为二次函数时,利用根与系数的关系解答.
解答:解:(1)当x=0时,y=1.
所以不论m为何值,函数y=mx2﹣6x+1的图象都经过y轴上一个定点(0,1);
(2)①当m=0时,函数y=﹣6x+1的图象与x轴只有一个交点;
②当m≠0时,若函数y=mx2﹣6x+1的图象与x轴只有一个交点,则方程mx2﹣6x+1=0有两个相等的实数根,
所以△=(﹣6)2﹣4m=0,m=9.
综上,若函数y=mx﹣6x+1的图象与x轴只有一个交点,则m的值为0或9.
点评:此题考查了抛物线与x轴的交点或一次函数与x轴的交点,是典型的分类讨论思想的应用.
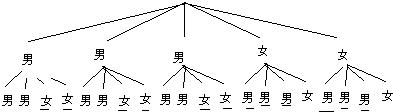
23、(2011•南京)从3名男生和2名女生中随机抽取2014年南京青奧会志愿者.求下列事件的概率:
(1)抽取1名,恰好是女生;
(2)抽取2名,恰好是1名男生和1名女生.
考点:列表法与树状图法;概率公式。
专题:数形结合。
分析:(1)女生人数除以学生总数即为所求概率;
(2)列举出所有情况,看恰好是1名男生和1名女生的情况数占总情况数的多少即可.
解答:解:(1)5名学生中有2名女生,,所以抽取1名,恰好是女生的概率为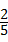 ;
;
(2)共有20种情况,恰好是1名男生和1名女生的情况数有12种,所以概率为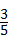 .
.
点评:考查求概率问题;用到的知识点为:概率=所求情况数与总情况数之比;得到所求的情况数是解决本题的关键.
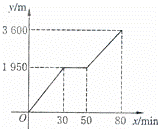
22、(2011•南京)小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中 的折线表示小亮在整个行走过程中y与x的函数关系.
(1)小亮行走的总路程是 3600 m,他途中休息了 20 min;
(2)①当50<x<80时,求y与x的函数关系式;②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
考点:一次函数的应用。
专题:应用题。
分析:(1)纵坐标为小亮行走的路程,其休息的时间为纵坐标不随x的值的增加而增加;
(2)根据当50<x<80时函数图象经过的两点的坐标,利用待定系数法求得函数的解析式即可.
解答:解:(1)3600,20;
(2)①当50≤x≤80时,设y与x的函数关系式为y=kx+b,
根据题意,当x=50时,y=1950;当x=80时,y=3600
∴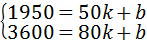
解得: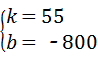
∴函数关系式为:y=55x﹣800.
②缆车到山顶的线路长为3600÷2=1800米,
缆车到达终点所需时间为1800÷180=10分钟
小颖到达缆车终点时,小亮行走的时间为10+50=60分钟,
把x=60代入y=55x﹣800,得y=55×60﹣800=2500
∴当小颖到达缆车终点时,小亮离缆车终点的路程是3600﹣2500=1100米.
点评:本题考查了一次函数的应用,解决此类题目最关键的地方是经过认真审题,从中整理出一次函数模型,用一次函数的知识解决此类问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com