
题目列表(包括答案和解析)
16、(2011•毕节地区)已知一次函数y=kx+3的图象如图所示,则不等式kx+3<0的解集是 x>1.5 .

考点:一次函数与一元一次不等式。
分析:本题需先求出一次函数y=kx+3的图象与x轴的交点坐标,再根据交点坐标即可求出不等式kx+3<0的解集.
解答:解:∵是(1.5,0),
∴不等式kx+3<0的解集是x>1.5.
故答案为:x>1.5.
点评:本题主要考查了一次函数与一元一次不等式的关系,在解题时要能根据函数的图象求不等式的解集是本题的关键.
15、(2011•毕节地区)如图,在△ABC中,AB=AC=10,CB=16,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )

A、50π﹣48 B、25π﹣48
C、50π﹣24 D、
考点:扇形面积的计算;等腰直角三角形。
专题:计算题。
分析:设以AB、AC为直径作半圆交BC于D点,连AD,根据直径所对的圆周角为直角得到AD⊥BC,再根据勾股定理计算出AD,然后利用阴影部分面积=半圆AC的面积+半圆AB的面积﹣△ABC的面积计算即可.
解答:解:设以AB、AC为直径作半圆交BC于D点,连AD,如图,
∴AD⊥BC,
∴BD=DC=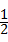 BC=8,
BC=8,
而AB=AC=10,CB=16,
∴AD= =
= =6,
=6,
∴阴影部分面积=半圆AC的面积+半圆AB的面积﹣△ABC的面积,
=π•52﹣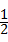 •16•8,
•16•8,
=25π﹣48.
故选B.
点评:本题考查了不规则图形面积的计算方法:把不规则的图形面积的计算转化为规则图形的面积和差来计算.也考查了圆周角定理的推论以及勾股定理.
14、(2011•毕节地区)如图,将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下,使木桩向上运动,已知楔子斜面的倾斜角为20°,若楔子沿水平方向前移8cm(如箭头所示),则木桩上升了( )

A、8tan20° B、
C、8sin20° D、8cos20°
考点:解直角三角形的应用-坡度坡角问题。
专题:几何综合题。
分析:根据已知,运用直角三角形和三角函数得到上升的高度为:8tan20°.
解答:解:由已知图形可得:
木桩上升的高度为:8tan20°.
故选A.
点评:此题考查的是解直角三角形的应用,关键是由已知得直角三角形,根据三角函数求解.
13、(2011•毕节地区)如图,已知AB=AC,∠A=36°,AB的中垂线MD交AC于点D、交AB于点M.下列结论:
①BD是∠ABC的平分线;
②△BCD是等腰三角形;
③△ABC∽△BCD;
④△AMD≌△BCD.
正确的有( )个.

A、4 B、3
C、2 D、1
考点:相似三角形的判定;全等三角形的判定;线段垂直平分线的性质;等腰三角形的判定与性质。
专题:几何综合题。
分析:首先由AB的中垂线MD交AC于点D、交AB于点M,求得△ABD是等腰三角形,即可求得∠ABD的度数,又由AB=AC,即可求得∠ABC与∠C的度数,则可求得所有角的度数,可得△BCD也是等腰三角形,则可证得△ABC∽△BCD.
解答:解:∵AB的中垂线MD交AC于点D、交AB于点M,
∴AD=BD,
∴∠ABD=∠A=36°,
∵AB=AC,
∴∠ABC=∠C=72°,
∴∠DBC=∠ABC﹣∠ABD=36°,
∴∠ABD=∠CBD,
∴BD是∠ABC的平分线;故①正确;
∴∠BDC=180°﹣∠DBC﹣∠C=72°,
∴∠BDC=∠C=72°,
∴△BCD是等腰三角形,故②正确;
∵∠C=∠C,∠BDC=∠ABC=72°,
∴△ABC∽△BCD,故③正确;
∵△AMD中,∠AMD=90°,△BCD中没有直角,
∴△AMD与△BCD不全等,故④错误.
故选B.
点评:此题考查了线段垂直平分线的性质,等腰三角形的性质,以及相似三角形的判定与性质等知识.此题综合性较强,但难度不大,解题的关键是注意数形结合思想的应用.
12、(2007•连云港)如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )

A、2cm B、 cm
cm
C、 D、
D、
考点:垂径定理;勾股定理。
分析:在图中构建直角三角形,先根据勾股定理得AD的长,再根据垂径定理得AB的长.
解答:解:作OD⊥AB于D,连接OA.
根据题意得OD=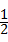 OA=1cm,
OA=1cm,
再根据勾股定理得:AD= cm,
cm,
根据垂径定理得AB=2 cm.
cm.
故选C.

点评:注意由题目中的折叠即可发现OD=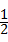 OA=1.考查了勾股定理以及垂径定理.
OA=1.考查了勾股定理以及垂径定理.
11、(2011•毕节地区)如图,已知AB∥CD,∠E=28°,∠C=52°,则∠EAB的度数是( )

A、28° B、52°
C、70° D、80°
考点:平行线的性质;三角形的外角性质。
分析:由AB∥CD,根据两直线平行,同位角相等,即可求得∠1的度数,又由三角形外角的性质,即可求得∠EAB的度数.
解答:解:∵ AB∥CD,
AB∥CD,
∴∠1=∠C=52°,
∵∠E=28°,
∴∠EAB=∠1+∠E=52°+28°=80°.
故选D.
点评:此题考查了平行线的性质.注意两直线平行,同位角相等,注意数形结合思想的应用.
10、(2011•毕节地区)广州亚运会期间,某纪念品原价168元,连续两次降价a%后售价为128元,下列所列方程正确的是( )
A、168(1+a%)2=128 B、168(1﹣a%)2=128
C、168(1﹣2a%)=128 D、168(1﹣a%)=128
考点:由实际问题抽象出一元二次方程。
专题:增长率问题。
分析:本题可先用168(1﹣a%)表示第一次降价后某纪念品的售价,再根据题意表示第二次降价后的售价,然后根据已知条件得到关于a的方程.
解答:解:当某纪念品第一次降价a%时,其售价为168﹣168a%=168(1﹣a%);
当某纪念品第二次降价a%后,其售价为168(1﹣a%)﹣168(1﹣a%)a%=168(1﹣a%)2.
∴168(1﹣a%)2=128.
故选B.
点评:本题主要考查一元二次方程的应用,要根据题意列出第一次降价后商品的售价,再根据题意列出第二次降价后售价的方程,令其等于128即可.
9、(2011•毕节地区)一次函数y=kx+k(k≠0)和反比例函数 在同一直角坐标系中的图象大致是( )
在同一直角坐标系中的图象大致是( )
A、 B、
B、
C、 D、
D、
考点:反比例函数的图象;一次函数的图象。
专题:探究型。
分析:分别根据反比例函数及一次函数图象的特点对各选项进行逐一分析即可.
解答:解:A、由反比例函数的图象在一、三象限可知k>0,由一次函数的图象过二、四象限可知k<0,两结论相矛盾,故本选项错误;
B、由反比例函数的图象在二、四象限可知k<0,由一次函数的图象与y轴交点在y轴的正半轴可知k>0,两结论相矛盾,故本选项错误;
C、由反比例函数的图象在二、四象限可知k<0,由一次函数的图象过二、三、四象限可知k<0,两结论一致,故本选项正确;
D、由反比例函数的图象在一、三象限可知k>0,由一次函数的图象与y轴交点在y轴的负半轴可知k<0,两结论相矛盾,故本选项错误.
故选C.
点评:本题考查的是一次函数与反比例函数图象的特点,熟知一次函数与反比例函数的性质是解答此题的关键.
8、(2011•毕节地区)函数 中自变量x的取值范围是( )
中自变量x的取值范围是( )
A、x≥﹣2 B、x≥﹣2且x≠1
C、x≠1 D、x≥﹣2或x≠1
考点:函数自变量的取值范围。
专题:函数思想。
分析:根据二次根式的性质和分式的意义,被开方数≥0,分母不等于0,就可以求解.
解答:解:根据题意得:被开方数x+2≥0,
解得x≥﹣2,
根据分式有意义的条件,x﹣1≠0,
解得x≠1,
故x≥﹣2且x≠1.
故选B.
点评:考查了函数自变量的取值范围,注意函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数为非负数.
7、两个相似多边形的面积比是9:16,其中小多边形的周长为36cm,则较大多边形的周长为( )
A、48cm B、54cm
C、56cm D、64cm
考点:相似多边形的性质。
分析:根据相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方计算即可.
解答:解:两个相似多边形的面积比是9:16,
面积比是周长比的平方,
则大多边形与小多边形的相似比是4:3.
相似多边形周长的比等于相似比,
因而设大多边形的周长为x,
则有 =
=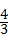 ,
,
解得:x=48.
大多边形的周长为48cm.
故选A.
点评:本题考查相似多边形的性质.相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com