
题目列表(包括答案和解析)
7.已知⊙O的半径为2cm,弦AB长为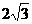 cm,则这条弦的中点到弦所对劣弧的中点的距离为
cm,则这条弦的中点到弦所对劣弧的中点的距离为
A 1 B 2 C 3 D 4 ( )
6.  、
、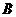 、
、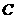 是平面内的三点,
是平面内的三点,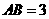 ,
,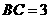 ,
,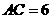 ,下列说法正确的是( )
,下列说法正确的是( )
A.可以画一个圆,使 、
、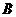 、
、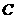 都在圆上
都在圆上
B.可以画一个圆,使 、
、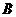 在圆上,
在圆上,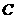 在圆外
在圆外
C.可以画一个圆,使 、
、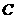 在圆上,
在圆上,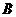 在圆外
在圆外
D.可以画一个圆,使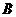 、
、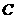 在圆上,
在圆上, 在圆内
在圆内
5.下列命题正确的是 ( ).
A.垂直于直径的直线是圆的切线
B.平分弧的直径垂直于弦,并且平分弦所对的弧
C.三点确定一个圆
D.在同圆或等圆中,同弧或等弧所对的圆周角相等
4. 已知⊙ 1与⊙
1与⊙ 2 相切,半径分别为
2 相切,半径分别为 和
和 ,则两圆的圆心距为 ( ).
,则两圆的圆心距为 ( ).
A. B.
B. C.
C. 或
或 D.
D. 或
或
3. 已知⊙ 的半径为3cm,圆心
的半径为3cm,圆心 到直线
到直线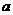 的距离为2cm,则直线
的距离为2cm,则直线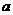 与⊙
与⊙ 的位置关系为
的位置关系为
A.相离 B.外切 C.相交 D.内切 ( )
2. 在同一时刻,身高1.6m的小强的影长是1.2m,旗杆的影长是15m,则旗杆高为 ( )
在同一时刻,身高1.6m的小强的影长是1.2m,旗杆的影长是15m,则旗杆高为 ( )
A、16m B、18m C、20m D、22m
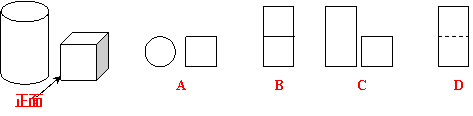
1.小明从正面观察下图所示的两个物体,看到的是 ( )
已知:如图,C为半圆上一点,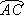 =
=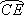 ,过点C作直径AB的垂线CP,P为垂足,弦AE分别交PC,CB于点D,F.
,过点C作直径AB的垂线CP,P为垂足,弦AE分别交PC,CB于点D,F.
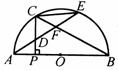 (1)求证:AD=CD;
(1)求证:AD=CD;
(2)若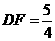 ,
,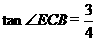 ,求PB的长.
,求PB的长.
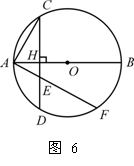
练习1、资阳市2005年如图6,已知AB为⊙O的直径,弦CD⊥AB,垂足为H.
(1) 求证:AH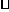 AB=AC2;
AB=AC2;
(2) 若过A的直线与弦CD(不含端点)相交于点E,与⊙O相交于点F,求证:AE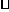 AF=AC2;
AF=AC2;
(3) 若过A的直线与直线CD相交于点P,与⊙O相交于点Q,判断AP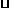 AQ=AC2是否成立(不必证明).
AQ=AC2是否成立(不必证明).
练习2、河南省2003年 已知:如图9,在直角梯形ABCD中AB//CD,AD⊥AB,以腰BC为直径的半圆O切AD于点E,连结点B、E,若BC=6,∠EBC=30°.
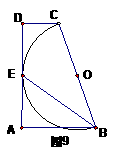 求梯形ABCD的面积.
求梯形ABCD的面积.
练习3、重庆市2003年高级中等学校招生统一考试(12分)如图:已知⊙O1和⊙O2 相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2 于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N。
 (1)过点A作AE∥CN交⊙O1于点E,求证:PA=PE;
(1)过点A作AE∥CN交⊙O1于点E,求证:PA=PE;
(2)连结PN,若PB=4,BC=2,求PN的长。
 练习4、北京市海淀区2003年高级中等学校招生考试
练习4、北京市海淀区2003年高级中等学校招生考试
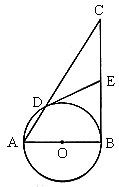
已知:以 的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连结DE。
的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连结DE。
(1)如图,求证:DE是⊙O的切线;
(2)连结OE,AE,当 为何值时,四边形AOED是平行四边形,并在此条件下求
为何值时,四边形AOED是平行四边形,并在此条件下求 的值。
的值。
(第(2)问答题要求:不要求写出解题过程,只需将结果填写在答题卡相应题号的横线上。)
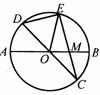 练习5、河南省2003年中考试卷(8分)
练习5、河南省2003年中考试卷(8分)
已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连结DE,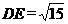 .
.
(1)求EM的长;
(2)求sin∠EOB的值.
 练习6、2002年黄冈市中考数学试题(9分)如图6,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连结OD,且∠AOD=∠APC.
练习6、2002年黄冈市中考数学试题(9分)如图6,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连结OD,且∠AOD=∠APC.
(1) 求证:AP是⊙O的切线;
(2) 若OC:CB=1:2,且AB=9,求⊙O的半径及sinA的值.
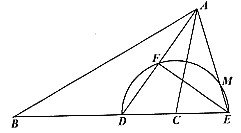
25. 已知:在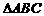 中,AD为
中,AD为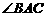 的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于点F,交AE于点M,且
的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于点F,交AE于点M,且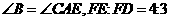 。
。
(1)求证: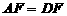
(2)求 的余弦值;
的余弦值;
(3)如果BD=10,求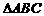 的面积。
的面积。
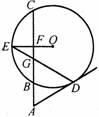 如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
(1)求证:AD是⊙O的切线;
(2)如果AB=2,AD=4,EG=2.求⊙O的半径.
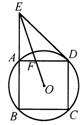 例二、陕西省2003年(本题满分8分)
例二、陕西省2003年(本题满分8分)
如图,正方形ABCD是⊙O的内接正方形,延长BA到E,使AE=AB,连结ED.
(1)求证:直线ED是⊙O的切线;
(2)连结EO交AD于点F,求证:EF=2FO.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com