
题目列表(包括答案和解析)
14、(2005年北京市海淀)已知抛物线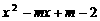 .
.
(1) 求证此抛物线与x轴有两个不同的交点;
(2)
若m是整数,抛物线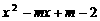 与x轴交于整数点,求m的值;
与x轴交于整数点,求m的值;
(3) 在(2)的条件下,设抛物线的顶点为A,抛物线与x轴的两个交点中右侧交点为B. 若m为坐标轴上一点,且MA=MB,求点M的坐标.
解:(1)证明:令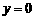 ,则
,则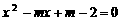 .因为
.因为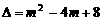 =
=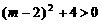 ,所以此抛物线与x轴有两个不同的交点. (2)因为关于x的方程
,所以此抛物线与x轴有两个不同的交点. (2)因为关于x的方程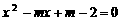 的根为
的根为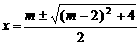 ,由m为整数,当
,由m为整数,当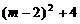 为完全平方数时,此抛物线与x轴才有可能交于整数点.设
为完全平方数时,此抛物线与x轴才有可能交于整数点.设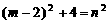 (其中n为整数),则
(其中n为整数),则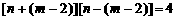 因为
因为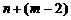 与
与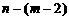 的奇偶性相同, 所以
的奇偶性相同, 所以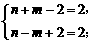 或
或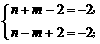 解得
解得 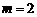 . 经过检验,当
. 经过检验,当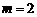 时,方程
时,方程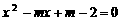 有整数根. 所以
有整数根. 所以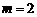 . (3)当m=2时,此二次函数解析式为
. (3)当m=2时,此二次函数解析式为
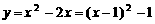 ,则顶点坐标为
,则顶点坐标为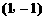 . 抛物线与x轴的交点为
. 抛物线与x轴的交点为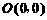 、
、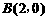 .
设抛物线的对称轴与x轴交于点
.
设抛物线的对称轴与x轴交于点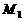 ,则
,则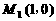 . 在直角三角形
. 在直角三角形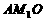 中,由勾股定理,得
中,由勾股定理,得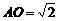 . 由抛物线的对称性可得,
. 由抛物线的对称性可得,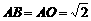 . 又
. 又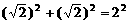 ,即
,即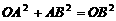 .所以△ABO为等腰直角三角形. 则
.所以△ABO为等腰直角三角形. 则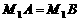 . 所以
. 所以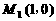 为所求的点. 若满足条件的点
为所求的点. 若满足条件的点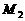 在y轴上时,设
在y轴上时,设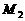 坐标为
坐标为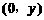 , 过A作AN⊥y轴于N,连结
, 过A作AN⊥y轴于N,连结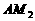 、
、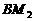 ,则
,则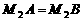 .由勾股定理,有
.由勾股定理,有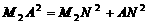 ;
;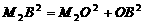 , 即
, 即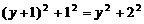 . 解得y=1. 所以
. 解得y=1. 所以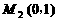 为所求的点. 综上所述,满足条件的M点的坐标为(1,0)或(0,1).
为所求的点. 综上所述,满足条件的M点的坐标为(1,0)或(0,1).
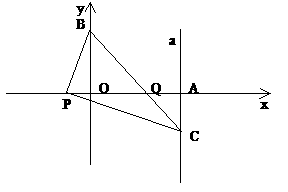
13、(丰台区2005)如图,已知平面直角坐标系中三点A(2,0),B(0,2),P(x,0)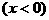 ,连结BP,过P点作
,连结BP,过P点作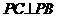 交过点A的直线a于点C(2,y)
交过点A的直线a于点C(2,y)
(1)求y与x之间的函数关系式;
(2)当x取最大整数时,求BC与PA的交点Q的坐标。
解:(1)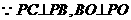
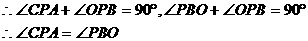
 A(2,0),C(2,y)在直线a上
A(2,0),C(2,y)在直线a上 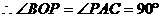
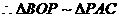
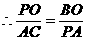 ,
,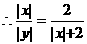 ,
, 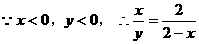
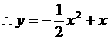 (2)
(2)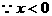 ,
,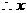 的最大整数值为
的最大整数值为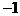 当
当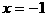 时,
时,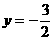 ,
,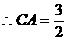
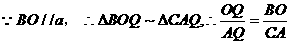 设Q点坐标为
设Q点坐标为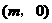 ,则
,则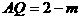
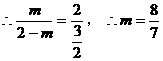
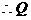 点坐标为
点坐标为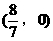
12、(丰台区2005)已知二次函数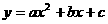 的图象如图所示,下列结论:
的图象如图所示,下列结论:
(1)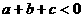 ;(2)
;(2)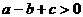 ;(3)
;(3)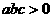 (4)
(4)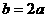 。其中正确的结论有:B
。其中正确的结论有:B
A. 4个 B. 3个 C. 2个 D. 1个
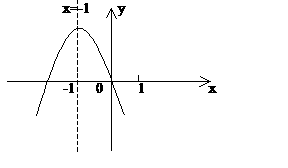
11、(南京市2005)在一块长方形镜面玻璃的四周镶上与它的周长相等的边框,制成一面镜子。镜子的长与宽的比是2:1。已知镜面玻璃的价格是每平方米120元,边框的价格是每米20元,另外制作这面镜子还需加工费45元。设制作这面镜子的总费用是y元,镜子的宽度是x米。
(1) 求y与x之间的关系式。
(2) 如果制作这面镜子共花了195元,求这面镜子的长和宽。
(1) y=240x2+180x+45 (2)长1m 宽0.5m
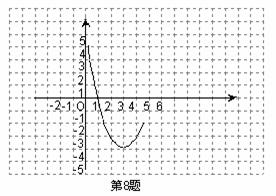
10、(枣 庄 市2005)已知抛物线y=ax2+bx+c经过点A(-2,7),B(6,7),C(3,-8),则该抛物线上纵坐标为-8的另一点的坐标是__(1,-8) _______·
9、(枣 庄 市2005)已知抛物线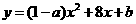 的图象的一部分如图所示,抛物线的顶点在第一象限,
的图象的一部分如图所示,抛物线的顶点在第一象限,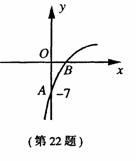 且经过点A(0,-7)和点B.
且经过点A(0,-7)和点B.
(1)求a的取值范围;
(2)若OA=2OB,求抛物线的解析式.
解:(1)由图可知,b=-7. 故抛物线为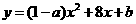 又抛物线的顶点在第一象限,开口向下,所以抛物线与x轴有两个不同的交点.
又抛物线的顶点在第一象限,开口向下,所以抛物线与x轴有两个不同的交点.
∴ 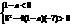 解之,得
解之,得 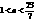 . 即a的取值范围是
. 即a的取值范围是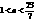 .
(2)设B(x1,o),由OA=20B,得7=2x1,即
.
(2)设B(x1,o),由OA=20B,得7=2x1,即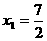 .
由于
.
由于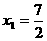 ,方程(1-a)x2+8x-7=o的一个根,∴
,方程(1-a)x2+8x-7=o的一个根,∴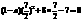 ∴
∴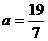 . 故所求所抛物线解析式为
. 故所求所抛物线解析式为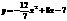 .
.
8、(2005常州市)已知抛物线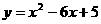 的部分图象如图,则抛物线的对称轴为直线x= 3
,满足y<0的x的取值范围是
1<x<5
,将抛物线
的部分图象如图,则抛物线的对称轴为直线x= 3
,满足y<0的x的取值范围是
1<x<5
,将抛物线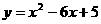 向 上
平移
4 个单位,则得到抛物线
向 上
平移
4 个单位,则得到抛物线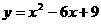 .
.
7、(2005年常德)某小型开关厂今年准备投入一定的经费用于现有生产设备的改造以提高经济效益.通过测算:今年开关的年产量y(万只)与投入的改造经费x(万元)之间满足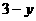 与
与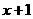 成反比例,且当改造经费投入1万元时,今年的年产量是2万只.
成反比例,且当改造经费投入1万元时,今年的年产量是2万只.
(1) 求年产量y(万只)与改造经费x(万元)之间的函数解析式.(不要求写出x的取值范围)
(2) 已知每生产1万只开关所需要的材料费是8万元.除材料费外,今年在生产中,全年还需支付出2万元的固定费用.
① 求平均每只开关所需的生产费用为多少元.(用含y的代数式表示)
(生产费用=固定费用+材料费)
② 如果将每只开关的销售价定位“平均每只开关的生产费用的1.5倍”与“平均每只开关所占改造费用的一半”之和,那么今年生产的开关正好销完.问今年需投入多少改造经费,才能使今年的销售利润为9.5万元?
(销售利润=销售收入-生产费用-改造费用)
(1)10(2)55(3)略(4)经观察所描各点,它们在二次函数的图象上。
设:此函数的解析式为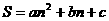 由题意得:
由题意得:
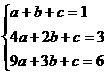 解得:
解得: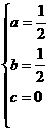
所以此函数的解析式为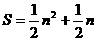
6、(2005年常德)请写出一个开口向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的解析式 y=(x-2)2+3等 。
5、(2005年常德)y=(x-1)2+2的对称轴是直线 ( B )
A.x=-1 B.x=1 C.y=-1 D.y=1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com