
题目列表(包括答案和解析)
解探索性试题需要灵活运用基础知识,大胆推理、联想、创新,恰当选用数形结合思想、转化思想和分类讨论等数学思想,多角度、多侧面、多层次思考问题,并考虑问题存在的各种可能性,从而揭示事物的整体性和一般性.
探索性试题往往没有明确的条件和结论,没有固定的形式和方法,要求学生通过观察、分析、比较、概括得出结论,其覆盖面广,综合性强,能力要求高.
探索性试题是近年来中考数学试题的一种新题型,也是热点题型,更是中考题多样化和时代发展要求的产物.一些省市连年考这种题型,而且在质量上也逐渐上一个新台阶,因此,在数学总复习时,必须重视这种题型.
32、(2005年太原)某市城建部门经过长期市场调查发现,该市年新建商品房面积P(万平方米)与市场新房均价x(千元/平方米)存在函数关系P=25x;年新房销售面积Q(万平方米)与市场新房均价x(千元/平方米)的函数关系为Q=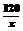 ―10;
―10;
(1)如果年新建商品房的面积与年新房销售面积相等,求市场新房均价和年新房销售总额;
(2)在(1)的基础上,如果市场新房均价上涨1千元,那么该市年新房销售总额是增加还是减少?变化了多少?结合年新房销售总额和积压面积的变化情况,请你提出一条合理化的建议。(字数不超过50)


31、(2005年太原) 已知二次函数y=ax2+bx+c的部分对应值如下表,求这个函数的解析式,并写出其图像的顶点坐标和对称轴。
|
x |
―2 |
―1 |
0 |
1 |
2 |
3 |
|
y |
0 |
―2 |
―2 |
0 |
4 |
10 |

30、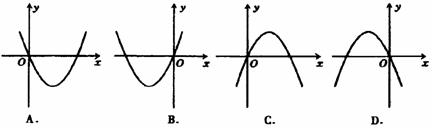 (2005年太原)在反比例函数y=
(2005年太原)在反比例函数y=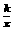 中,当x>0时,y随x的增大而增大,则二次函数y=kx2+2kx的图像大致是( D )
中,当x>0时,y随x的增大而增大,则二次函数y=kx2+2kx的图像大致是( D )
29、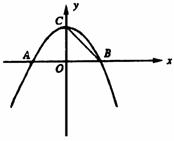 (贵州省毕节地区2005) 如图,抛物线y=―
(贵州省毕节地区2005) 如图,抛物线y=―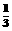 x2+(6―
x2+(6―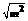 )x+m―3与x轴交于A(x1,0)、B(x2,0)两点(x1<x2),交y轴于C点,且x1+x2=0。
)x+m―3与x轴交于A(x1,0)、B(x2,0)两点(x1<x2),交y轴于C点,且x1+x2=0。
(1)求抛物线的解析式,并写出顶点坐标及对称轴方程。
(2)在抛物线上是否存在一点P使△PBC≌△OBC,
若存在,求出点P的坐标,若不存在,请说明理由。

28、(贵州省毕节地区2005)当你将一把扇形扇子逐渐打开时,容易发现打开部分的扇形面积随圆心角的变化而变化,那么下列函数中能正确描述这种变化的是( A )
A.正比例函数 B.反比例函数 C.一次函数(b≠0) D.二次函数
27、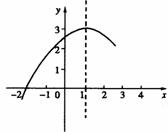 (2005年湖南省湘潭)如图;抛物线y=ax2+bx+c(a≠0)的图像与x轴的一个交点是(-2,0),顶点是(1,3)。下列说法中不正确的是( )
(2005年湖南省湘潭)如图;抛物线y=ax2+bx+c(a≠0)的图像与x轴的一个交点是(-2,0),顶点是(1,3)。下列说法中不正确的是( )
A.抛物线的对称轴是x=1
B.抛物线的开口向下
C.抛物线与x轴的另一个交点是(2,0)
D.当x=1时,y有最大值是3
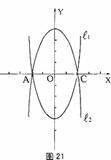
26、(玉溪市2005)如图21,已知抛物线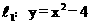 的图象与x轴交于A、C两点。
的图象与x轴交于A、C两点。
(1)若抛物线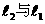 关于x轴对称,求
关于x轴对称,求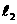 的解析式;
的解析式;
(2)若点B是抛物线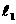 上一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点记为D,求证:点D在
上一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点记为D,求证:点D在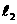 上;
上;
(3)探索:当点B分别位于 在x轴上、下两部分的图象上时,□ABCD的面积是否存在最大值或最小值?若存在,判断它是何种特殊平行四边形并求出它的面积;若不存在,请说明理由。
在x轴上、下两部分的图象上时,□ABCD的面积是否存在最大值或最小值?若存在,判断它是何种特殊平行四边形并求出它的面积;若不存在,请说明理由。
解:(1)设 的解析式为y=
的解析式为y=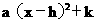 .
.
∵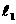 与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),
与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),
并且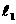 与
与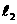 关于x轴对称,
关于x轴对称,
∴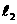 经过点A(-2,0),C(2,0),顶点坐标是(0,4).
经过点A(-2,0),C(2,0),顶点坐标是(0,4).
∴y=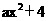 .
.
∴0=4a+4 得a=-1,
∴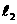 的解析式为
的解析式为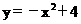 .
.
(2)设B(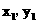 )
)
∵点B在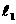 上,
上,
∴B(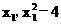 )
)
∵四边形ABCD是平行四边形,A、C关于O对称。
∴B、D关于原点O对称,
∴D(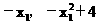 ).
).
将D(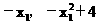 )的坐标代入
)的坐标代入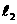 :
: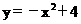
可知 左边=右边。
∴点D在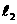 上。
上。
(3)设□ABCD的面积为S,则S=2×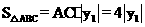 .
.
(I)当点B在x轴上方时,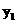 >0,
>0,
∴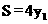 ,它是关于
,它是关于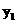 的正比例函数且S随
的正比例函数且S随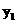 的增大而增大,
的增大而增大,
∴S既无最大值也无最小值。
(II)当点B在x轴下方时,-4≤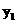 <0.
<0.
∴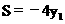 ,它是关于
,它是关于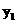 的正比例函数且S随
的正比例函数且S随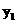 的增大而减小,
的增大而减小,
∴当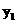 =-4时,S有最大值16,但它没有最小值。
=-4时,S有最大值16,但它没有最小值。
此时B(0,-4)在y轴上,它的对称点D也在y轴上。
∴AC⊥BD.
∴□ABCD是菱形。此时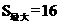 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com