
题目列表(包括答案和解析)
33、(湖州市2004)方程组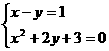 的解是(B )
的解是(B )

32、(2004年富阳)已知一个长方体的木箱高为80 ,底面的长比宽多10
,底面的长比宽多10 ,(1)求这个长方体的体积
,(1)求这个长方体的体积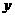 (
(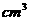 )与长方体的宽
)与长方体的宽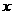 (
( )之间的函数关系式;(2)问当该木箱的体积为0.72
)之间的函数关系式;(2)问当该木箱的体积为0.72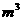 时,木箱底面的长与宽各为多少
时,木箱底面的长与宽各为多少 ?
?
解:(1)因为木箱的长、宽、高分别为: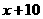
 、
、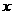
 、80
、80 ……2分
……2分
所以 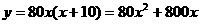
(2)因为 0.72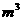 =720000
=720000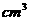
所以 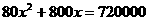 即
即 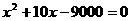
解得: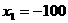 (舍去)
(舍去)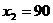
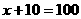
所以当木箱体积为0.72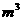 时,底面的长和宽分别为100
时,底面的长和宽分别为100 和90
和90 。
。
31、(2004年富阳)解下列方程:
(1)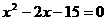 (2)
(2)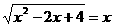
30、(郴州市2004)今年,我国政府为减轻农民负担,决定在5年内免去农业税.某乡今年人均上缴农业税25元,若两年后人均上缴农业税为16元,假设这两年降低的百分率相同.
(1)求降低的百分率;(2)若小红家有4人,明年小红家减少多少农业税?(3)小红所在的乡约有16000农民,问该乡农民明年减少多少农业税.
(1)设降低的百分率为x,
依题意有 解得x1=0.2=20%,x2 =1.8(舍去)
(2)小红全家少上缴税 25×20%×4=20(元)
(3)全乡少上缴税 16000×25×20%=80000(元)
29、(郴州市2004)方程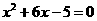 的左边配成完全平方后所得方程为 ( A )
的左边配成完全平方后所得方程为 ( A )
A. 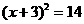 B.
B. 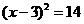 C.
C. 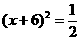 D. 以上答案都不对
D. 以上答案都不对
28、(日照市2004)方程组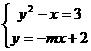 只有一个实数解,则实数
只有一个实数解,则实数 的值是 -1/6 ,-1/2,0
的值是 -1/6 ,-1/2,0
26、(2004年南通)已知关于x的一元二次方程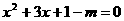
⑴请选取一个你喜爱的m的值,使方程有两个不相等的实数根,并说明它的正确性;
⑵设x1,x2是⑴中所得方程的两个根,求x1x2+x1+x2的值。
所取m值要满足m>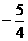 下略
下略
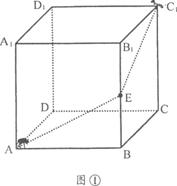
※※※27、(淮安市2004) 如图①,一个无盖的正方体盒子的棱长为10厘米,顶点C1处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙.(盒壁的厚度忽略不计)
(1)假设昆虫甲在顶点C1处静止不动,如图①,在盒子的内部我们先取棱BB1的中点E,
再连结AE、EC1.昆虫乙如果沿路径A-E-C1爬行,那么可以在最短的时间内捕捉到昆虫
甲.仔细体会其中的道理,并在图①中画出另一条路径,使昆虫乙从顶点A沿这条路径爬行,同样可以在最短的时间内捕捉到昆虫甲.(请简要说明画法)
(2)如图②,假设昆虫甲从顶点C1,以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?(精确到1秒)
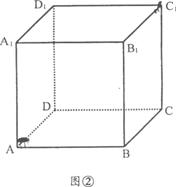
别为各棱中点) (说明:无画法,扣2分)
(2)由(1)可知,当昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙可以沿下列四
种路径中的任意一种爬行:
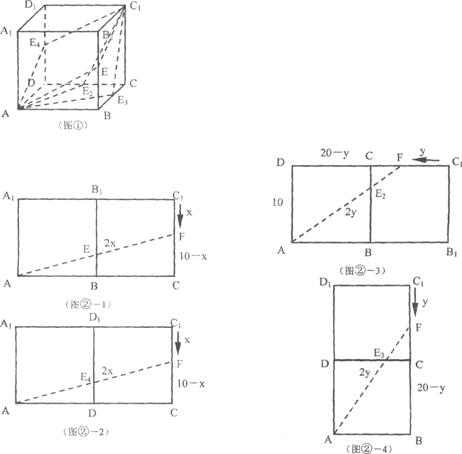
可以看出,图②-1与图②-2中的路径相等,图②-3与图②-4中的路径相等.
①设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F
爬行捕捉到昆虫甲需x秒钟,如图②-1-1,在Rt△ACF中,
(2x)2=(10-x)2+202,解得x=10;
设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E2→F
爬行捕捉到昆虫甲需y秒钟,如图②-1-2,在Rt△ABF中,
(2y)2=(20-y)2+102,解得y=8;
所以昆虫乙从顶点A爬行捕捉到昆虫甲至少需8秒钟.
[说明]未考虑到A→E→F和图④中其它路径,而直接按路径A→E→F(或A→E→F)
计算,并求出正确答案的不扣分.
25、(2004年南通)解方程组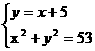
24、(南昌市2004)已知关于x的方程x2-2(m+1)x+m2=0.
(1)当m取什么值时,原方程没有实数根;
(2)对m选取一个合适的非零整数,使原方程有两个实数根,并求这两个实数根的平方和.
解:(1)△=[-2(m+1)]2-4m2 ………………………………………………………1分
=4(m2+2m+1)-4m2
=4(2m+1)<0. ……………………………………………………… 2分
∴m<-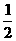 .
.
当m<-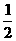 时,原方程没有实数根; …………………………………………………3分
时,原方程没有实数根; …………………………………………………3分
(2)取m=1时,原方程为x2-4x+1=0.…………………………………………………4分
设此方程的两实数根为x1, x2,则x1+x2=4, x1·x2=1.…………………………………5分
∴x12+x22=(x1+x2)2-2x1x2=42-2×1=14.
23、(2004年龙岩) 某商品标价1200元,打八折售出后仍盈利100元,则该商品进价是B
(A)800元 (B)860元 (C)900元 (D)960元
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com