
题目列表(包括答案和解析)
5、二次函数 的图象向上平移2个单位,得到新的图象的二次函数表达式是(
)
的图象向上平移2个单位,得到新的图象的二次函数表达式是(
)
A、 B、
B、 C、
C、 D、
D、
4、下列图形中,既是轴对称图形,又是中心对称图形是( )




A B C D
3、据《法制日报》2006年6月8日报道,1996年至2004年8年间全国耕地面积减少114000000亩,用科学记数法表示为 ( )
A.1.14×106 B.1.14×107 C.1.14×108 D.0.114×109
2、 某物体的三视图是如图所示的三个图形,那么该物体形状是( )
某物体的三视图是如图所示的三个图形,那么该物体形状是( )
A、长方体 B、圆锥体
C、立方体 D、圆柱体
1.如果□ ,那么“□”内应填的实数是( )
,那么“□”内应填的实数是( )
A. B.
B. C.
C. D.
D. 
13.据中新社报道:2010年我国粮食产量将达到540 000 000 000 kg,用科学记数法表示这个粮食产量为
kg。
14.已知关于x的不等式组 的整数解共有6个,则a的取值范围是
。
的整数解共有6个,则a的取值范围是
。
 15.如图,已知⊙O中,直径MN=10,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45°,则AB的长为
。
15.如图,已知⊙O中,直径MN=10,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45°,则AB的长为
。
16.如图,已知反比例函数 的图像上有一点P,过点P分别作x轴和y轴的垂线,垂足分别为A、B,使四边形OAPB为正方形。又在反比例函数的图像上有一点P1,过点P1分别作BP和y轴的垂线,垂足分别为A1、B1,使四边形BA1P1B1为正方形,则点P1的坐标是
。
的图像上有一点P,过点P分别作x轴和y轴的垂线,垂足分别为A、B,使四边形OAPB为正方形。又在反比例函数的图像上有一点P1,过点P1分别作BP和y轴的垂线,垂足分别为A1、B1,使四边形BA1P1B1为正方形,则点P1的坐标是
。
01.函数 中,自变量x的取值范围是( )。
中,自变量x的取值范围是( )。
A、x≥-1 B、x>2 C、x>-1且x≠2 D、x≥-1且x≠2
|


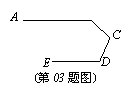
03.如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°,∠D=120°,则∠C的度数为( )。
A、120° B、100° C、140° D、90°
04.小华把自己一周的支出情况用如图所示的统计图表示出来,下列说法中,正确的是( )。
 A、从图中可以直接看出具体的消费数额
A、从图中可以直接看出具体的消费数额
B、从图中可以直接看出总消费数额
C、从图中可以直接看出各项消费数额占总消费数额的百分比
D、从图中可以直接看出各项消费数额在一周中的具体变化情况
05.化简 =( )。
=( )。
 A、
A、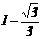 B、
B、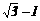 C、
C、 D、
D、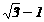
06.使用同一种规格的下列地砖,不能密铺的是( )。
A、正六边形地砖 B、正五边形地砖 C、正方形地砖 D、正三角形地砖
07.关于x的不等式2x-a≤-1的解集如图所示,则a的取值是( )。
A、0 B、-3 C、-2 D、-1
08.如图,一块实验田的形状是三角形(设其为△ABC),管理员从BC边上的一点D出发,沿DC→CA→AB→BD的方向走了一圈回到D处,则管理员从出发到回到原处在途中身体( )。
 A、转过90° B、转过180° C、转过270° D、转过360°
A、转过90° B、转过180° C、转过270° D、转过360°


09.抛物线 与x轴的两个不同交点是O和A,顶点B在直线
与x轴的两个不同交点是O和A,顶点B在直线 上,则关于△OAB的判断正确的是( )。
上,则关于△OAB的判断正确的是( )。
A、等腰三角形 B、直角三角形 C、等边三角形 D、等腰直角三角形
10.甲、乙两名同学在一次用频率去估计概率的实验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( )。
A、掷一枚正六面体的骰子,出现1点的概率
B、从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
C、抛一枚硬币,出现正面的概率
D、任意写一个整数,它能被2整除的概率
11.如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若⊙O的圆心在线段BP上,且⊙O与AB、AC都相切,则⊙O的半径是( )。
A、1 B、 C、
C、 D、
D、
12.中百超市推出如下优惠方案:(1)一次性购物不超过100元,不享受优惠;(2)一次性购物超过100元,但不超过300元一律9折;(3)一次性购物超过300元一律8折。某人两次购物分别付款80元、252元,如果他将这两次所购商品一次性购买,则应付款( )。
A、288元 B、332元 C、288元或316元 D、332元或363元
1。同角(或等角)的余角相等。 3。对顶角相等。 5。三角形的一个外角等于和它不相邻的两个内角之和。 6。在同一平面内垂直于同一条直线的两条直线是平行线。 7。同位角相等,两直线平行。 12。等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合。 16。直角三角形中,斜边上的中线等于斜边的一半。 19。在角平分线上的点到这个角的两边距离相等。及其逆定理。 21。夹在两条平行线间的平行线段相等。夹在两条平行线间的垂线段相等。 22。一组对边平行且相等、或两组对边分别相等、或对角线互相平分的四边形是平行四边形。 24。有三个角是直角的四边形、对角线相等的平行四边形是矩形。 25。菱形性质:四条边相等、对角线互相垂直,并且每一条对角线平分一组对角。 27。正方形的四个角都是直角,四条边相等。两条对角线相等,并且互相垂直平分,每一条对角线平分一组对角。 34。在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对相等,那么它们所对应的其余各对量都相等。 36。垂直于弦的直径平分这条弦,并且平分弦所对弧。平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧。 43。直角三角形被斜边上的高线分成的两个直角三角形和原三角形相似。 46。相似三角形对应高线的比,对应中线的比和对应角平分线的比都等于相似比。相似三角形面积的比等于相似比的平方。 37.圆内接四边形的对角互补,并且任何一个外角等于它的内对角。 47。切线的判定定理 经过半径的外端并且垂直于这条半径的直线是圆的切线。 48。切线的性质定理①经过圆心垂直于切线的直线必经过切点。 ②圆的切线垂直于经过切点的半径。 ③经过切点垂直于切线的直线必经过圆心。 49。切线长定理 从圆外一点引圆的两条切线,它们的切线长相等。连结圆外一点和圆心的直线,平分从这点向圆所作的两条切线所夹的角。 50。弦切角定理 弦切角的度数等于它所夹的弧的度数的一半。弦切角等于它所夹的弧所对的圆周角。 51。相交弦定理 ; 切割线定理 ; 割线定理
101圆是定点的距离等于定长的点的集合 102圆的内部可以看作是圆心的距离小于半径的点的集合 103圆的外部可以看作是圆心的距离大于半径的点的集合 104同圆或等圆的半径相等 105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆 106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线 107到已知角的两边距离相等的点的轨迹,是这个角的平分线 108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线 109定理 不在同一直线上的三个点确定一条直线 110垂径定理 垂直于弦的直径平分这条弦并且平分弦所对的两条弧 111推论1 ①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧 ②弦的垂直平分线经过圆心,并且平分弦所对的两条弧 ③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
112推论2 圆的两条平行弦所夹的弧相等 113圆是以圆心为对称中心的中心对称图形 114定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等 115推论 在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等 116定理 一条弧所对的圆周角等于它所对的圆心角的一半 117推论1 同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等 118推论2 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径 119推论3 如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形 120定理 圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角 121①直线L和⊙O相交 d﹤r ②直线L和⊙O相切 d=r ③直线L和⊙O相离 d﹥r 122切线的判定定理 经过半径的外端并且垂直于这条半径的直线是圆的切线 123切线的性质定理 圆的切线垂直于经过切点的半径 124推论1 经过圆心且垂直于切线的直线必经过切点 125推论2 经过切点且垂直于切线的直线必经过圆心 126切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角 127圆的外切四边形的两组对边的和相等 128弦切角定理 弦切角等于它所夹的弧对的圆周角 129推论 如果两个弦切角所夹的弧相等,那么这两个弦切角也相等 130相交弦定理 圆内的两条相交弦,被交点分成的两条线段长的积相等 131推论 如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项 132切割线定理 从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项 133推论 从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等 134如果两个圆相切,那么切点一定在连心线上
135①两圆外离 d﹥R+r ②两圆外切 d=R+r ③两圆相交 R-r﹤d﹤R+r(R﹥r) ④两圆内切 d=R-r(R﹥r) ⑤两圆内含d﹤R-r(R﹥r) 136定理 相交两圆的连心线垂直平分两圆的公共弦 137定理 把圆分成n(n≥3): ⑴依次连结各分点所得的多边形是这个圆的内接正n边形 ⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形 138定理 任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆 139正n边形的每个内角都等于(n-2)×180°/n 140定理 正n边形的半径和边心距把正n边形分成2n个全等的直角三角形 141正n边形的面积Sn=pnrn/2 p表示正n边形的周长 142正三角形面积√3a/4 a表示边长 143如果在一个顶点周围有k个正n边形的角,由于这些角的和应为360°,因此k×(n-2)180°/n=360°化为(n-2)(k-2)=4 144弧长计算公式:L=n∏R/180 145扇形面积公式:S扇形=n∏R/360=LR/2 146内公切线长= d-(R-r) 外公切线长= d-(R+r)
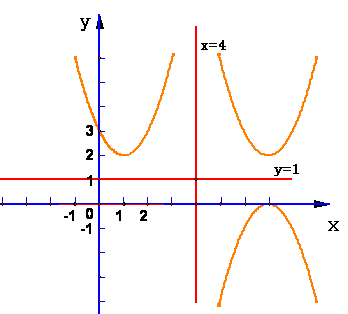
27、如图在一张纸上作出二次函数y = x2 – 2x + 3的图象,沿x=4把这张纸对折,描出抛物线y = x2 – 2x + 3关于x=4对称的抛物线y1。将得到的抛物线再次沿y=1对折一次得到的抛物线y2。若有一条直线y = kx
+ b与y交于A、B两点与y2交于C、D两点。且AB=CD=
(1)求 y1 、 y2 所表示的二次函数。
(2)此时y与y2的图象的位置关系是怎样的?
(3)求直线y = kx + b的解析式
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com