
题目列表(包括答案和解析)
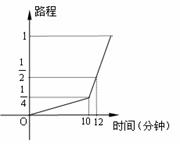
3.已知 为实数,且
为实数,且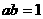 ,设
,设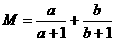 ,
,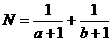 ,则
,则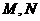 的大小关系是( )
的大小关系是( )
 A.
A.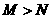 B.
B.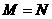 C.
C.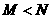 D.无法确定
D.无法确定
2.如图,边长为1的正方形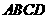 绕点
绕点 逆时针旋转
逆时针旋转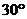 到正方形
到正方形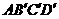 ,图中阴影部分的面积为( )
,图中阴影部分的面积为( )
A.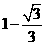 B.
B.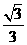 C.
C.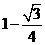 D.
D.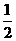
1. 计算
计算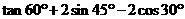 的结果是( )
的结果是( )
A.2 B.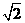 C.1 D.
C.1 D.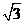
29、(本题9分)
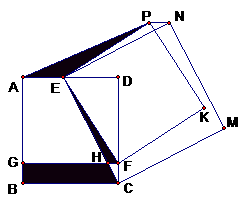
矩形ABCD中,点E从A点出发沿AD向右运动,点F从C出发沿CD向上运动。点E的速度为2个单位每秒,点F的速度为1个单位每秒。现两点同时出发,t秒钟后到达如图位置。过F作FG∥BC,交AB于G,交EC于H。四边形ECMN和EFKP都是正方形。
(1) 猜想PN与AD的位置关系并加以证明;(4分)
(2) 若S -S
-S =10,S
=10,S =8,求t的值。(5分)
=8,求t的值。(5分)
28、 (本题9分)
(本题9分)
如图:梯形ABCD中,AD∥BC,AD⊥AB ,AD=AB=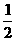 BC=4,E、F分别在BC、DC上,将梯形沿EF折叠,点C恰好落在点A上。
BC=4,E、F分别在BC、DC上,将梯形沿EF折叠,点C恰好落在点A上。
(1) 求BE的长;(3分)
(2) 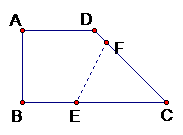 设AD和EF的延长线交于G,试说明⊿AEG是等腰三角形;(2分)
设AD和EF的延长线交于G,试说明⊿AEG是等腰三角形;(2分)
(3) 求EF的长。(4分)
27、(本题8分)
某化工材料经销公司购进了一种化工原料共7000千克,购进价格为每千克30元。物价部门规定其销售单价不得高于每千克70元,也不得低于30元。市场调查发现:单价定为70元时,日均销售60千克;单价每降低1元,日均多售出2千克。在销售过程中,每天还要支出其它费用500元(天数不足一天时,按整天计算)。设销售单价为x元,日均获利为y元。
(1)求y关于x的二次函数关系式(化简并关于x降幂排列),注明x的取值范围;
(2)结合(1)中所求出的二次函数分析,指出单价定为多少元时日均获利最多,是多少?
(3)若将这种化工原料全部售出,比较日均获利最多和销售单价最高这两种销售方式,哪一种获总利较多,多多少?
26、(本题8分)
已知二次函数y=-x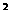 -(m-3)x+m的图象与直线y=kx+12(k<0)交于x轴上同一点,直线与两坐标轴围成的面积是12。
-(m-3)x+m的图象与直线y=kx+12(k<0)交于x轴上同一点,直线与两坐标轴围成的面积是12。
(1) 求m的值
(2) 若二次函数图象上有一点C,抛物线与x轴交于A、B两点,且S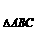 =3,求点C的坐标。
=3,求点C的坐标。
25、 (本题6分)
(本题6分)
某商场设立了一个可以自由转动的转盘,并规定:顾客购物满50元就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(如果指针正好指在分界线上,则重转一次),下表是活动进行中的一组统计数据:
|
转动转盘的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
|
落在“可乐”的次数m |
43 |
64 |
83 |
203 |
325 |
401 |
落在“可乐”的频率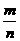 |
0.43 |
0.427 |
0.415 |
0.415 |
0.406 |
0.401 |
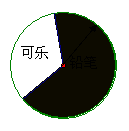 (1)请估计,当n很大时,频率
(1)请估计,当n很大时,频率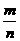 将会接近多少?(2分)
将会接近多少?(2分)
答: (结果保留2位有效数字)。
(2)某顾客一次消费了258元,按照规定他可以抽5次奖,他获取的5件奖品中,可乐很可能是几罐?(2分)
答: 罐。
(3)同学小红和小丽在商场玩,她们想借这位顾客的摇奖结果打一个赌,为此她们设
计了一个比赛规则。请你在下面的比赛规则中填写合适的数字,使比赛显得公平:
答:如果顾客转到可乐,那么小红得3分;如果转到铅笔,那么小丽得 分。(2分)
24、(本题8分)
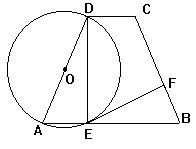
如图,在梯形ABCD中,AB∥DC,AD=BC,以AD为直径的圆O交AB于点E,圆O的切线EF交BC于点F。 求证:(1)∠DEF=∠B;(2)EF⊥BC
23、(本题6分)
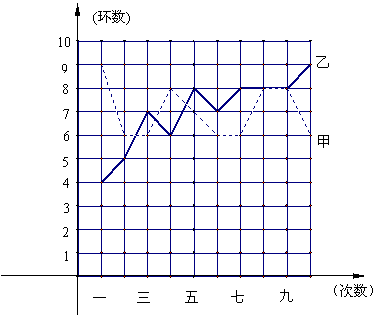 某校业余射击集训队近几年的比赛成绩一直不很理想,为此,学校利用2004年暑期进行集训,希望今年能有所进步。在为期一个月的集训期间,对甲、乙两名运动员进行了10次测试,成绩如右图所示:
某校业余射击集训队近几年的比赛成绩一直不很理想,为此,学校利用2004年暑期进行集训,希望今年能有所进步。在为期一个月的集训期间,对甲、乙两名运动员进行了10次测试,成绩如右图所示:
(1)根据右图提供的信息填写下表:
|
|
平均数 |
众数 |
方差 |
|
甲 |
7 |
|
1.2 |
|
乙 |
|
|
2.2 |
(2)教练员将以上射击成绩与以往比赛结果对比以后发现,如果以现有成绩参加比赛,今年的成绩仍然不容乐观,必须在比赛前最后阶段进行强化训练。由于条件限制,只能留下一名运动员。请你帮助教练员分析一下,应留下哪一位运动员继续训练?简要说明理由。
答:应留下 (填“甲”或“乙”);因为:
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com