
题目列表(包括答案和解析)
7.视图与投影:会画基本几何体(直棱柱、圆柱、圆锥、球)的三视图(主视图、左视图、俯视图),会判断简单物体的三视图,能根据三视图描述基本几何体或实物原型;了解直棱柱、圆锥的侧面展开图,能根据展开图判断和制作立体模型;了解基本几何体与其三视图、展开图(球除外)之间的关系.
[热点透视]
热点1:平行线的性质及角的计算的考查
例1 (2008株州)如图1,已知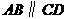 ,直线MN分别交AB、CD于E、F,
,直线MN分别交AB、CD于E、F,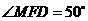 ,
,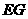 平分∠MEB,那么∠MEG的大小是_________度.
平分∠MEB,那么∠MEG的大小是_________度.
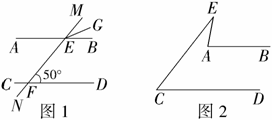
分析:本题根据两直线平行,同位角相等可得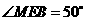 ,再利用角平分线的定义迅速求得∠MEG的大小.
,再利用角平分线的定义迅速求得∠MEG的大小.
解:25.
点评:本题考查了平行线的性质和角平分线及其性质,这种类型的题注重双基,注重通性通法,在试题难度上属容易题,学生解题时能迅速上手.
热点2:平行线的性质与三角形知识相联系的考查
例2 (2008永州)如图2所示,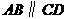 ,
,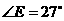 ,
,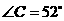 ,则
,则 的度数为( )
的度数为( )
(A)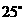 (B)
(B)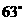
(C)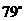 (D)
(D)
分析:本题延长EA交CD于点F,则将求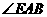 的度数转化为求
的度数转化为求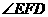 的度数,利用三角形外角的性质可迅速求解.
的度数,利用三角形外角的性质可迅速求解.
解:选(C).
点评:本题亦可延长BA或连结CA并延长,构造三角形求解,考查了平行线的性质及三角形内角及外角的性质,具有一定的综合性.
热点3:三角形角之间关系的考查
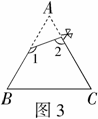 例3 (2008永州)如图3,已知
例3 (2008永州)如图3,已知 中,
中,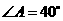 ,剪去
,剪去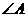 后成四边形,则
后成四边形,则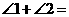 ______.
______.
分析:本题先利用三角形的内角和求出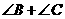 ,再利用四边形的内角和可求得
,再利用四边形的内角和可求得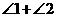 .
.
解: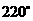 .
.
点评:本题考查三角形的内角与外角的关系,可以从多个角度思考,既可利用三角形的内角和定理,也可利用四边形的内角和定理来解决此问题.从多个角度着手解题是数学试题的共同特点.
热点4:三角形与其他知识的联系的考查
例4 (2008长沙)已知点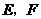 在
在 的边
的边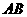 所在的直线上,且
所在的直线上,且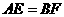 ,
,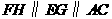 ,
,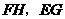 分别交边
分别交边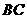 所在的直线于点
所在的直线于点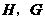 .
.
(1)如图4,如果点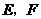 在边
在边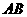 上,那么
上,那么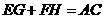 ;
;
(2)如图5,如果点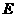 在边
在边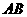 上,点
上,点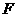 在
在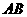 的延长线上,那么线段
的延长线上,那么线段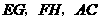 的长度关系是_______;
的长度关系是_______;
(3)如图6,如果点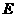 在
在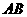 的反向延长线上,点
的反向延长线上,点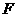 在
在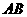 的延长线上,那么线段
的延长线上,那么线段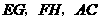 的长度关系是_______.
的长度关系是_______.
对(1)(2)(3)三种情况的结论,请任选一个给予证明.
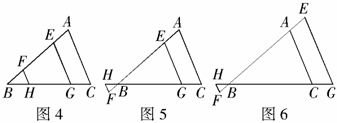
分析:构造全等三角形是解决本题的关键.
解:(2)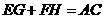 ;(3)
;(3)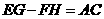 ;
;
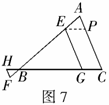 证明(2):如图7,过点
证明(2):如图7,过点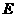 作
作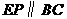 交AC于
交AC于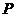 ,
,
∵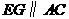 ,
,
∴四边形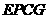 为平行四边形.
为平行四边形.
∴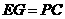 .
.
∵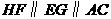 ,
,
∴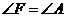 ,
,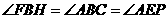 .
.
又∵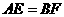 ,∴
,∴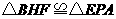 .
.
∵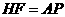 ,∴
,∴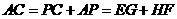 ,即
,即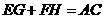 .
.
点评:本题考查同学们对三角形全等及平行四边形的有关性质与识别等知识的把握.本题将合情推理与演绎推理有机的结合在一起,通过同学们的观察、类比思考后,提出猜想,进而利用“截长补短”的方法加以论证;而且本题证明时只要求三选一,给同学们提供了广阔的思维空间,这也是近几年,尤其新课程改革后的一种时尚考法.
热点5:多边形的内角和、外角和及平面密铺等基础知识的考查
例5 (2008长沙)正五边形的一个内角的度数是____________.
分析:正五边形的每个内角都相等是解决这个问题的关键.
解: .
.
点评:本题考查同学们对n边形的内角和为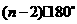 及正多边形的概念这两个知识点的综合应用,立足基础,注重实效.
及正多边形的概念这两个知识点的综合应用,立足基础,注重实效.
例6 (2008岳阳)在美丽的岳阳南湖广场中心地带整修工程中,计划采用同一种正多边形地板砖铺砌地面,在下列形状的地板砖:①正方形;②正五边形;③正六边形;④正八边形中,能够铺满地面的地板砖的种数有( )
(A)1种 (B)2种 (C)3种 (D)4种
分析:本题应先求出各正多边形的每个内角的度数,再依据平面密铺的条件作出正确的选择.
解:选(B).
点评:本题考查了同学们对平面密铺的条件的把握,要求在每个接合点处正好围成 的角,谨记“不重不漏”.
的角,谨记“不重不漏”.
 热点6:平行四边形、矩形、菱形、正方形、等腰梯形的性质与判定的考查
热点6:平行四边形、矩形、菱形、正方形、等腰梯形的性质与判定的考查
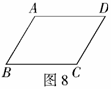
例7 (2008长沙)如图8,四边形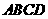 中,
中,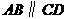 ,要使四边形
,要使四边形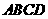 为平行四边形,则应添加的条件是________(添加一个条件即可).
为平行四边形,则应添加的条件是________(添加一个条件即可).
分析:本题可从四边形的边、角两方面来寻找判定该四边形为平行四边形的方法.
解:答案不惟一,如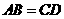 或
或 等.
等.
点评:本题是一道开放性的问题,在答案不确定的情况下考查同学们对平行四边形的判定方法的掌握,这是近几年新课改后比较经典的考法.
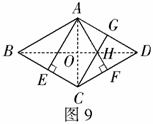 例8 如图9,菱形
例8 如图9,菱形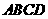 中,
中,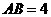 ,
,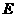 为
为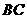 的中点,
的中点,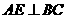 ,
,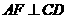 于点
于点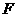 ,
,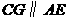 ,
,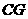 交
交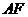 于点
于点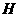 ,交
,交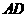 于点
于点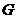 .
.
(1)求菱形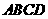 的面积;
的面积;
(2)求 的度数.
的度数.
解:(1)连结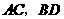 ,相交于点
,相交于点 ,
,
∵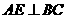 ,且
,且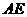 平分
平分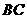 ,
,
∴ 和
和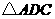 都是正三角形.∴
都是正三角形.∴ .
.
因为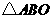 是直角三角形,∴
是直角三角形,∴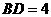 .
.
∴菱形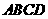 的面积是8.
的面积是8.
(2)∵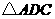 是正三角形,
是正三角形,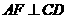 ,∴
,∴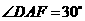 .
.
又∵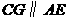 ,
,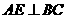 ,∴四边形
,∴四边形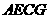 是矩形.
是矩形.
∴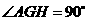 .∴
.∴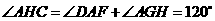 .
.
点评:菱形(矩形)面积计算一般通过计算对角线求解.本题综合了菱形性质,等边三角形的判定和菱形面积、角度计算.
热点7:圆的有关概念、点与圆、直线与圆、圆与圆位置关系的考查
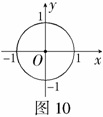 例9 (2008常德)如图10,在直角坐标系中,
例9 (2008常德)如图10,在直角坐标系中, 的半径为1,
的半径为1,
则直线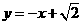 与
与 的位置关系是( )
的位置关系是( )
(A)相离 (B)相交
(C)相切 (D)以上三种情形都有可能
分析:本题关键是要求出点O到直线的距离.
解:选(C).
点评:本题主要考查同学们对直线与圆的三种位置关系的判定依据的掌握程度,常利用圆心到直线的距离d与圆的半径r之间的大小关系来判定.
热点8:圆的切线的性质与判定的运用的考查
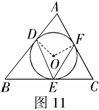 例10 (2008娄底)已知
例10 (2008娄底)已知 的内切圆
的内切圆 ,如图11,
,如图11,
若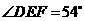 ,则
,则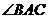 等于( )
等于( )
(A)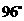 (B)
(B)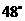
(C)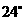 (D)
(D)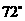
分析:本题先利用同圆中同弧所对的圆周角等于它所对圆心角的一半求得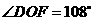 ,再利用切线的性质便可求
,再利用切线的性质便可求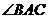 的度数.
的度数.
解:选(D).
点评:本题主要考查了圆的切线的性质及圆中同弧所对的圆周角与圆心角之间的关系.
 热点9:与圆有关的计算问题的考查
热点9:与圆有关的计算问题的考查
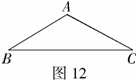
例11 (2008衡阳)如图12,一块呈三角形的草坪上,一小孩将绳子一端栓住兔子,另一端套在木桩 处.若
处.若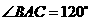 ,绳子长3米(不包括两个栓处用的绳子),则兔子在草坪上活动的最大面积是( )
,绳子长3米(不包括两个栓处用的绳子),则兔子在草坪上活动的最大面积是( )
(A)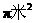 (B)2
(B)2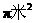 (C)3
(C)3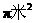 (D)9
(D)9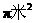
分析:本题中兔子在草坪上活动的最大面积即为半径为3米,圆心角为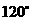 的扇形的面积.
的扇形的面积.
解:选(C).
点评:本题从同学们熟悉的生活情境入手,考查同学们对扇形面积的求法,注重理论联系实际,体现了数学来源于生活,又为生活实践服务的新课程理念.
热点10:考查尺规作图中的五种基本作图及其在实际中的应用.
例12 (2008永州)近年来,国家实施“村村通”工程和农村医疗卫生改革,某县计划在张村、李村之间建一座定点医疗站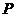 ,张、李两村座落在两相交公路内(如图13所示).医疗站必须满足下列条件:①使其到两公路距离相等,②到张、李两村的距离也相等,请你通过作图确定P点的位置.
,张、李两村座落在两相交公路内(如图13所示).医疗站必须满足下列条件:①使其到两公路距离相等,②到张、李两村的距离也相等,请你通过作图确定P点的位置.
分析:要“使其到两公路距离相等”其实就是作角平分线,要“到张、李两村的距离相等”其实就是作两点连线的垂直平分线,它们的交点就是所求作的点.
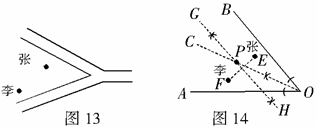
解:如图14,(1)画出角平分线;(2)作出垂直平分线.点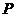 即为所求.
即为所求.
点评:此题是要求用作图法解决有关实际问题,掌握五种基本作图是解决此类题的关键.
热点11:采用灵活多变的方式,考查基本几何体与其三视图、展开图之间的关系.
例 13 (2008岳阳)下面的三个图形是某几何体的三种视图,则该几何体是( )
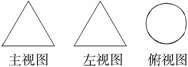
(A)正方体 (C)圆柱体
(C)圆锥体 (D)球体
分析:根据三种视图的特点,由图可判断该物体形状为圆锥体.
解: 选(C).
点评:本题是由三种视图推断立体图形,其关键是“读图”,同时对常见几何体的三种视图也要熟悉.
热点12:直棱柱、圆锥的侧面展开图
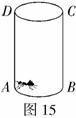 例14 (2008怀化)如图15所示的圆柱体中底面圆的半径是
例14 (2008怀化)如图15所示的圆柱体中底面圆的半径是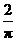 ,高为2,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是______.(结果保留根号)
,高为2,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是______.(结果保留根号)
分析:本题是圆柱的侧面展开图知识的应用,圆柱的侧面展开图是一个矩形,并能将这矩形的长与宽跟圆柱的高(或母线)、底面圆半径找到相互转化的对应关系.
解: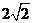 .
.
点评:圆柱、圆锥的侧面展开图渗透了化曲面为平面,化立体图形为平面图形的“转化”的思想,要注意它们展开前后相关数据之间的对应关系.
热点13:考查应用中心投影与平行投影解决有关实际问题.
例15 (2008益阳)在一次数学活动课上,李老师带领同学们去测教学楼的高度.在阳光下,测得身高1.65m的黄丽同学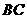 的影长
的影长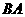 为1.1m,与此同时,测得教学楼
为1.1m,与此同时,测得教学楼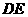 的影长
的影长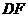 为12.1m.
为12.1m.
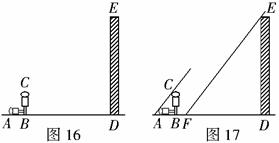
(1)请你在图16中画出此时教学楼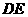 在阳光下的投影
在阳光下的投影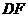 ;
;
(2)请你根据已测得的数据,求出教学楼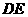 的高度(精确到0.1m).
的高度(精确到0.1m).
分析:本题是平行投影的有关知识,根据题意,作出两个相似三角形是解答本题的关键.
解:(1)在图17中,连结 ,过
,过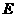 点作
点作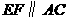 交
交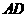 于
于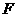 ,则
,则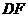 为所求.
为所求.
(2)由平行投影知,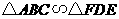 ,则
,则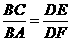 ,
,
∴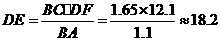 (m).
(m).
即教学楼的高度约为18.2m.
点评:本题考查的是投影和相似三角形在实际问题中的综合应用,这要求同学们不仅要掌握基本知识,还要学会将其应用到实际问题中,体现了新课标考查综合应用能力的要求.
[考题预测]
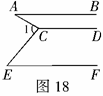 1.如图18,
1.如图18, ,
,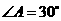 ,
,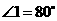 ,
,
则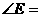 _________度.
_________度.
6.尺规作图:能完成以下基本作图:作一条线段等于已知线段,作一个角等于已知角,作角的平分线,作线段的垂直平分线,过一点作垂线;能利用基本作图作三角形:已知三边作三角形;已知两边及其夹角作三角形;已知两角及其夹边作三角形;已知底边及底边上的高作等腰三角形;会探索如何过一点、两点和不在同一直线上的三点作圆.了解尺规作图的步骤,对于尺规作图题,会写已知、求作和作法(不要求证明).
5.圆:有关概念,如:弧、弦、圆心角、圆周角等及其它们之间的关系;点与圆、直线与圆、圆与圆之间的位置关系,切线的性质及判定;与圆有关的计算,如求弧长、扇形的面积、圆锥的侧面积与全面积等.
4.四边形:对平行四边形、矩形、菱形、正方形、等腰梯形的性质与判定,了解多边形的内角和与外角和公式、正多边形的概念,平面的密铺及其简单设计等.
3.三角形:三角形的边角关系及三角形的分类;三角形的角平分线、中线、高线、中位线等重要线段的性质;全等三角形的性质与判定;等腰三角形的性质与判定;等边三角形的性质;直角三角形中的勾股定理及其逆定理等.
2.平行线与相交线:线段垂直平分线及性质;相交线中“两线四角”及“三线八角”中形成的对顶角、同位角、内错角、同旁内角等角与角之间的关系;平行线的性质及判定;平行线间的距离及平行线、垂线的画法等.
1.角:会计算角度;认识度、分、秒,会进行简单的换算;了解角平分线及其性质.
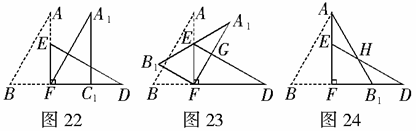
8.如图19,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图20),量得他们的斜边长为10cm,较小锐角为 ,再将这两张三角形纸片摆成如图21的形状,但点
,再将这两张三角形纸片摆成如图21的形状,但点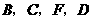 在同一条直线上,且点
在同一条直线上,且点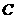 与点
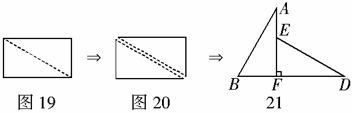
与点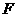 重合(在图21至图24中统一用
重合(在图21至图24中统一用 表示).
表示).
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图21中的 沿BD向右平移到图22的位置,使点
沿BD向右平移到图22的位置,使点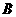 与点
与点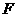 重合,请你求出平移的距离;
重合,请你求出平移的距离;
(2)将图21中的 绕点F顺时针方向旋转
绕点F顺时针方向旋转 到图23的位置,
到图23的位置,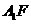 交DE于点G,请你求出线段FG的长度;
交DE于点G,请你求出线段FG的长度;
(3)将图21中的 沿直线AF翻折到图24的位置,
沿直线AF翻折到图24的位置,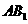 交DE于点H,请证明:
交DE于点H,请证明: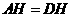 .
.
6.如图17, 中
中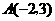 ,
,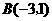 ,
,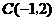 .
.
(1)将 向右平移4个单位长度,画出平移后的
向右平移4个单位长度,画出平移后的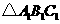 ;
;
(2)画出 关于x轴对称的
关于x轴对称的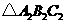 ;
;
(3)将 绕原点
绕原点 旋转
旋转 ,画出旋转后的
,画出旋转后的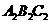 ;
;
(4)在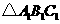 ,
,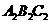 ,
, 中,△______与△______成轴对称,对称轴是_________.
中,△______与△______成轴对称,对称轴是_________.
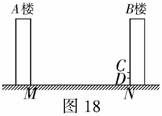 7.如图18,某居民小区内
7.如图18,某居民小区内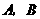 两楼之间的距离
两楼之间的距离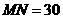 米,两楼的高都是20米,
米,两楼的高都是20米, 楼在
楼在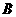 楼正南,
楼正南,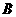 楼窗户朝南.
楼窗户朝南.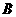 楼内一楼住户的窗台离小区地面的距离
楼内一楼住户的窗台离小区地面的距离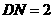 米,窗户高
米,窗户高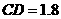 米.当正午时刻太阳光线与地面成
米.当正午时刻太阳光线与地面成 角时,
角时, 楼的影子是否影响
楼的影子是否影响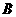 楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.(参考数据:
楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.(参考数据: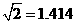 ,
,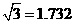 ,
,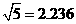 )
)
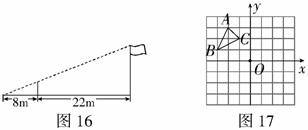
5.如图16了测量学校旗杆的高度,小东用长为3.2的竹竿做测量工具,移动竹竿,使竹杆、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为__________m.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com