
题目列表(包括答案和解析)
24. 解:(1)∵点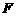 在
在 上,
上,
∴ ,
,
∴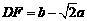 ,
,
∴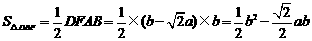 .
.
(2)连结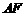 , 由题意易知
, 由题意易知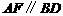 ,
,
∴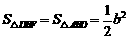 .
.
(3)正方形AEFG在绕A点旋转的过程中,F点的轨迹是以点A为圆心,AF为半径的圆.
第一种情况:当b>2a时,存在最大值及最小值;
因为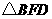 的边
的边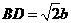 ,故当F点到BD的距离取得最大、最小值时,
,故当F点到BD的距离取得最大、最小值时,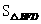 取得最大、最小值.
取得最大、最小值.
如图②所示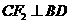 时,
时,
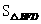 的最大值=
的最大值=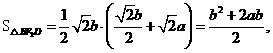
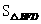 的最小值=
的最小值=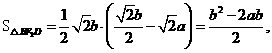
第二种情况:当b=2a时,存在最大值,不存在最小值;
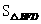 的最大值=
的最大值=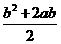 .(如果答案为4a2或b2也可)
.(如果答案为4a2或b2也可)

23. 解(Ⅰ)当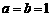 ,
,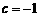 时,抛物线为
时,抛物线为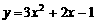 ,
,
方程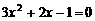 的两个根为
的两个根为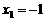 ,
,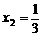 .
.
∴该抛物线与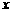 轴公共点的坐标是
轴公共点的坐标是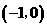 和
和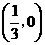 . ················································ 2分
. ················································ 2分
(Ⅱ)当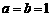 时,抛物线为
时,抛物线为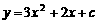 ,且与
,且与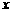 轴有公共点.
轴有公共点.
对于方程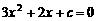 ,判别式
,判别式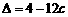 ≥0,有
≥0,有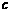 ≤
≤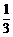 . ········································ 3分
. ········································ 3分
①当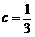 时,由方程
时,由方程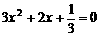 ,解得
,解得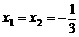 .
.
此时抛物线为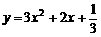 与
与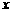 轴只有一个公共点
轴只有一个公共点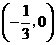 .·································
4分
.·································
4分
②当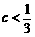 时,
时,
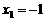 时,
时, ,
,
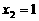 时,
时,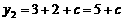 .
.
由已知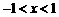 时,该抛物线与
时,该抛物线与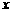 轴有且只有一个公共点,考虑其对称轴为
轴有且只有一个公共点,考虑其对称轴为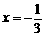 ,
,
应有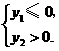 即
即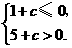
解得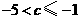 .
.
综上,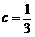 或
或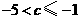 . ················································································ 6分
. ················································································ 6分
(Ⅲ)对于二次函数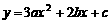 ,
,
由已知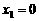 时,
时,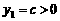 ;
;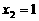 时,
时,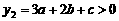 ,
,
又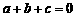 ,∴
,∴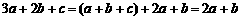 .
.
于是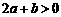 .而
.而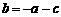 ,∴
,∴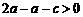 ,即
,即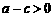 .
.
∴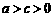 . ············································································································ 7分
. ············································································································ 7分
∵关于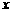 的一元二次方程
的一元二次方程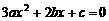 的判别式
的判别式
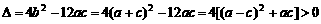 ,
,
 ∴抛物线
∴抛物线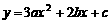 与
与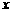 轴有两个公共点,顶点在
轴有两个公共点,顶点在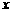 轴下方.····························· 8分
轴下方.····························· 8分
又该抛物线的对称轴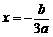 ,
,
由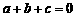 ,
,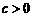 ,
,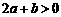 ,
,
得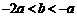 ,
,
∴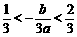 .
.
又由已知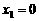 时,
时,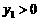 ;
;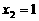 时,
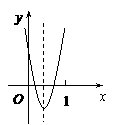
时,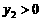 ,观察图象,
,观察图象,
可知在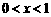 范围内,该抛物线与
范围内,该抛物线与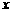 轴有两个公共点. ············································ 10分
轴有两个公共点. ············································ 10分
22. 解:( 1)由已知得:
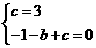 解得
解得
c=3,b=2
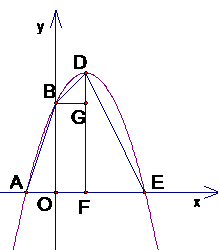 ∴抛物线的线的解析式为
∴抛物线的线的解析式为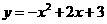
(2)由顶点坐标公式得顶点坐标为(1,4)
所以对称轴为x=1,A,E关于x=1对称,所以E(3,0)
设对称轴与x轴的交点为F
所以四边形ABDE的面积=
=
=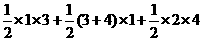
=9
(3)相似
如图,BD=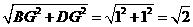
BE=
DE=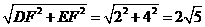
所以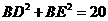 ,
, 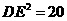 即:
即: 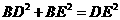 ,所以
,所以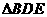 是直角三角形
是直角三角形
所以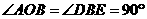 ,且
,且 ,
,
所以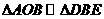 .
.
21.解:
(1)m=-5,n=-3
(2)y=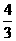 x+2
x+2
(3)是定值.
因为点D为∠ACB的平分线,所以可设点D到边AC,BC的距离均为h,
设△ABC AB边上的高为H,
则利用面积法可得:
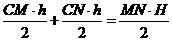
(CM+CN)h=MN﹒H
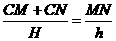
又 H=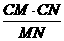
化简可得 (CM+CN)﹒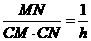
故 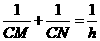
20. 解:(1)如图,过点B作BD⊥OA于点D.
在Rt△ABD中,
∵∣AB∣=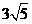 ,sin∠OAB=
,sin∠OAB=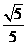 ,
,
∴∣BD∣=∣AB∣·sin∠OAB
=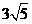 ×
×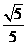 =3.
=3.
又由勾股定理,得
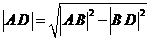
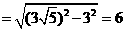
∴∣OD∣=∣OA∣-∣AD∣=10-6=4.
∵点B在第一象限,∴点B的坐标为(4,3). ……3分
设经过O(0,0)、C(4,-3)、A(10,0)三点的抛物线的函数表达式为
y=ax2+bx(a≠0).
由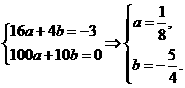
∴经过O、C、A三点的抛物线的函数表达式为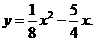 ……2分
……2分
(2)假设在(1)中的抛物线上存在点P,使以P、O、C、A为顶点的四边形为梯形
①∵点C(4,-3)不是抛物线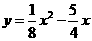 的顶点,
的顶点,
∴过点C做直线OA的平行线与抛物线交于点P1 .
则直线CP1的函数表达式为y=-3.
对于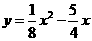 ,令y=-3
,令y=-3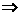 x=4或x=6.
x=4或x=6.
∴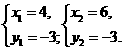
而点C(4,-3),∴P1(6,-3).
在四边形P1AOC中,CP1∥OA,显然∣CP1∣≠∣OA∣.
∴点P1(6,-3)是符合要求的点. ……1分
②若AP2∥CO.设直线CO的函数表达式为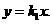
将点C(4,-3)代入,得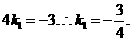
∴直线CO的函数表达式为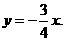
于是可设直线AP2的函数表达式为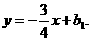
将点A(10,0)代入,得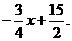
∴直线AP2的函数表达式为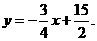
由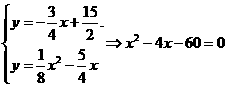 ,即(x-10)(x+6)=0.
,即(x-10)(x+6)=0.
∴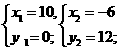
而点A(10,0),∴P2(-6,12).
过点P2作P2E⊥x轴于点E,则∣P2E∣=12.
在Rt△AP2E中,由勾股定理,得
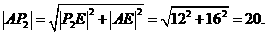
而∣CO∣=∣OB∣=5.
∴在四边形P2OCA中,AP2∥CO,但∣AP2∣≠∣CO∣.
∴点P2(-6,12)是符合要求的点. ……1分
③若OP3∥CA,设直线CA的函数表达式为y=k2x+b2
将点A(10,0)、C(4,-3)代入,得
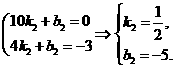
∴直线CA的函数表达式为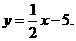
∴直线OP3的函数表达式为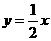
由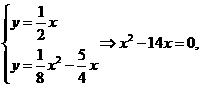 即x(x-14)=0.
即x(x-14)=0.
∴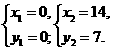
而点O(0,0),∴P3(14,7).
过点P3作P3E⊥x轴于点E,则∣P3E∣=7.
在Rt△OP3E中,由勾股定理,得
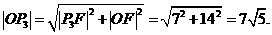
而∣CA∣=∣AB∣=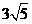 .
.
∴在四边形P3OCA中,OP3∥CA,但∣OP3∣≠∣CA∣.
∴点P3(14,7)是符合要求的点. ……1分
综上可知,在(1)中的抛物线上存在点P1(6,-3)、P2(-6,12)、P3(14,7),
使以P、O、C、A为顶点的四边形为梯形. ……1分
(3)由题知,抛物线的开口可能向上,也可能向下.
①当抛物线开口向上时,则此抛物线与y轴的副半轴交与点N.
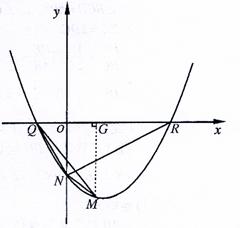 可设抛物线的函数表达式为
可设抛物线的函数表达式为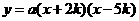 (a>0).
(a>0).
即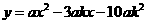
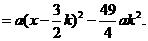
如图,过点M作MG⊥x轴于点G.
∵Q(-2k,0)、R(5k,0)、G(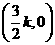 、N(0,-10ak2)、M
、N(0,-10ak2)、M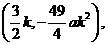
∴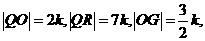
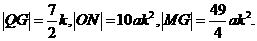
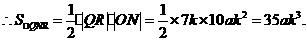
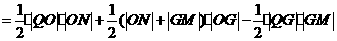
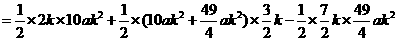
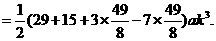
∴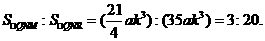 ……2分
……2分
②当抛物线开口向下时,则此抛物线与y轴的正半轴交于点N,
同理,可得 ……1分
……1分
综上所知,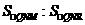 的值为3:20.
……1分
的值为3:20.
……1分
19. 解:(1)在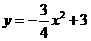 中,令
中,令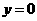
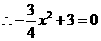
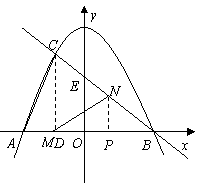
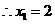 ,
,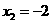
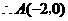 ,
,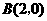 ····················································· 1分
····················································· 1分
又 点
点 在
在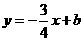 上
上
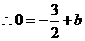
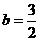
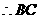 的解析式为
的解析式为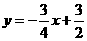 ···················································································· 2分
···················································································· 2分
(2)由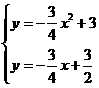 ,得
,得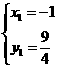
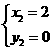 ·························································· 4分
·························································· 4分
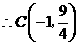 ,
,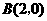
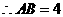 ,
,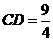 ····································································································· 5分
····································································································· 5分
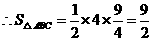 ······························································································· 6分
······························································································· 6分
(3)过点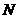 作
作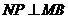 于点
于点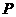
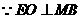
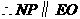
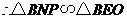 ····································································································· 7分
····································································································· 7分
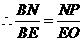 ················································································································ 8分
················································································································ 8分
由直线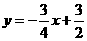 可得:
可得: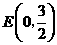
 在
在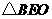 中,
中,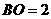 ,
,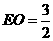 ,则
,则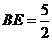
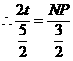 ,
,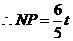 ····························································································· 9分
····························································································· 9分
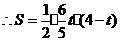
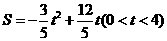 ·························································································· 10分
·························································································· 10分
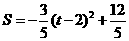 ··································································································· 11分
··································································································· 11分
 此抛物线开口向下,
此抛物线开口向下, 当
当 时,
时,
 当点
当点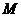 运动2秒时,
运动2秒时,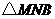 的面积达到最大,最大为
的面积达到最大,最大为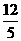 .
.
18. 解:(1)点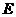 在
在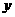 轴上························································································· 1分
轴上························································································· 1分
理由如下:
连接 ,如图所示,在
,如图所示,在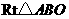 中,
中,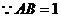 ,
,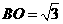 ,
,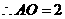
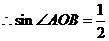 ,
,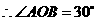
由题意可知: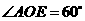
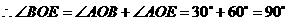
 点
点 在
在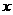 轴上,
轴上, 点
点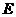 在
在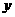 轴上.············································································ 3分
轴上.············································································ 3分
(2)过点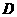 作
作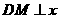 轴于点
轴于点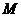
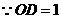 ,
,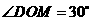
 在
在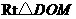 中,
中,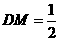 ,
,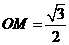
 点
点 在第一象限,
在第一象限,
 点
点 的坐标为
的坐标为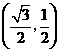 ····························································································· 5分
····························································································· 5分
由(1)知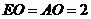 ,点
,点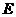 在
在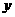 轴的正半轴上
轴的正半轴上
 点
点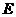 的坐标为
的坐标为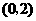
 点
点 的坐标为
的坐标为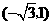 ······························································································· 6分
······························································································· 6分
 抛物线
抛物线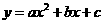 经过点
经过点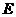 ,
,
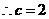
由题意,将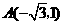 ,
,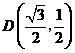 代入
代入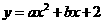 中得
中得
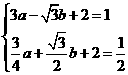 解得
解得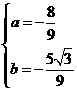
 所求抛物线表达式为:
所求抛物线表达式为: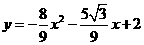 ·························································· 9分
·························································· 9分
(3)存在符合条件的点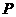 ,点
,点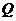 .············································································ 10分
.············································································ 10分
理由如下: 矩形
矩形 的面积
的面积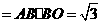
 以
以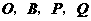 为顶点的平行四边形面积为
为顶点的平行四边形面积为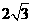 .
.
由题意可知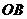 为此平行四边形一边,
为此平行四边形一边,
又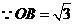
 边上的高为2······································································································ 11分
边上的高为2······································································································ 11分
依题意设点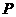 的坐标为
的坐标为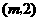
 点
点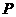 在抛物线
在抛物线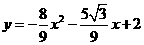 上
上
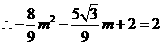
解得,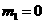 ,
,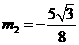
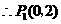 ,
,
 以
以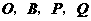 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
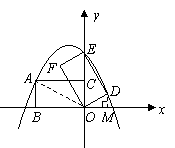
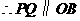 ,
,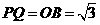 ,
,
 当点
当点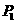 的坐标为
的坐标为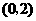 时,
时,
点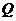 的坐标分别为
的坐标分别为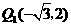 ,
,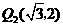 ;
;
当点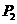 的坐标为
的坐标为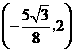 时,
时,
点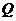 的坐标分别为
的坐标分别为 ,
,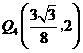 .·················································· 14分
.·················································· 14分
(以上答案仅供参考,如有其它做法,可参照给分)
17. 解:(1) 直线
直线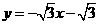 与
与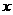 轴交于点
轴交于点 ,与
,与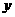 轴交于点
轴交于点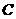 .
.
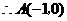 ,
,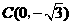 ······························································································· 1分
······························································································· 1分
 点
点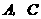 都在抛物线上,
都在抛物线上,
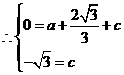
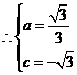
 抛物线的解析式为
抛物线的解析式为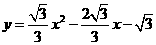 ······························································ 3分
······························································ 3分
 顶点
顶点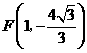 ····································································································· 4分
····································································································· 4分
(2)存在····················································································································· 5分
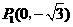 ··················································································································· 7分
··················································································································· 7分
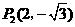 ·················································································································· 9分
·················································································································· 9分
(3)存在···················································································································· 10分
理由:
解法一:
延长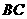 到点
到点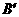 ,使
,使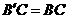 ,连接
,连接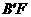 交直线
交直线 于点
于点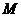 ,则点
,则点 就是所求的点.
就是所求的点.
··························································································· 11分
 过点
过点 作
作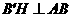 于点
于点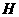 .
.
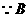 点在抛物线
点在抛物线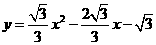 上,
上,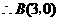
在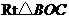 中,
中,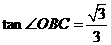 ,
,
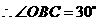 ,
,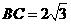 ,
,
在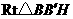 中,
中,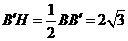 ,
,
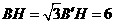 ,
,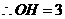 ,
,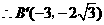 ····················································· 12分
····················································· 12分
设直线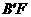 的解析式为
的解析式为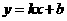
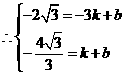 解得
解得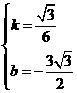
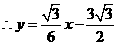 ······································································································ 13分
······································································································ 13分
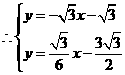 解得
解得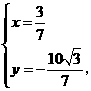

 在直线
在直线 上存在点
上存在点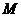 ,使得
,使得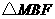 的周长最小,此时
的周长最小,此时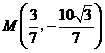 .········· 14分
.········· 14分
解法二:
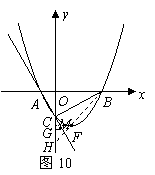 过点
过点 作
作 的垂线交
的垂线交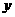 轴于点
轴于点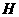 ,则点
,则点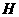 为点
为点 关于直线
关于直线 的对称点.连接
的对称点.连接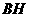 交
交 于点
于点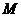 ,则点
,则点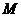 即为所求.···················································································· 11分
即为所求.···················································································· 11分
过点 作
作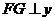 轴于点
轴于点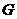 ,则
,则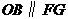 ,
,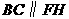 .
.
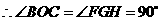 ,
,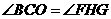
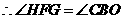
同方法一可求得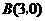 .
.
在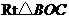 中,
中,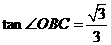 ,
,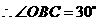 ,可求得
,可求得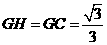 ,
,
 为线段
为线段 的垂直平分线,可证得
的垂直平分线,可证得 为等边三角形,
为等边三角形,
 垂直平分
垂直平分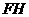 .
.
即点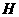 为点
为点 关于
关于 的对称点.
的对称点.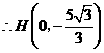 ··················································· 12分
··················································· 12分
设直线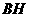 的解析式为
的解析式为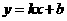 ,由题意得
,由题意得
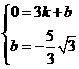 解得
解得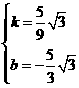
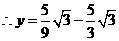 ······································································································ 13分
······································································································ 13分
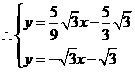 解得
解得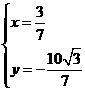

 在直线
在直线 上存在点
上存在点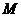 ,使得
,使得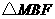 的周长最小,此时
的周长最小,此时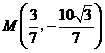 . 1
. 1
16.
解:(1)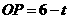 ,
,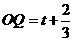 .
.
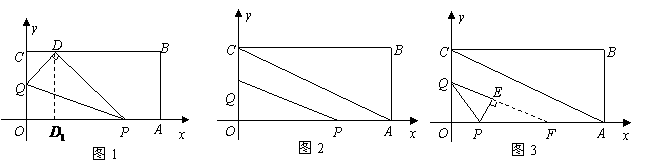

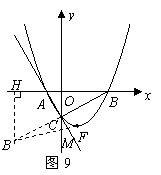
(2)当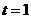 时,过
时,过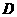 点作
点作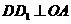 ,交
,交 于
于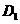 ,如图1,
,如图1,
则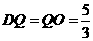 ,
,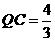 ,
,
 ,
,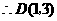 .
.
(3)①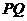 能与
能与 平行.
平行.
若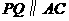 ,如图2,则
,如图2,则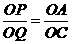 ,
,
即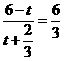 ,
,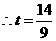 ,而
,而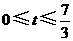 ,
,
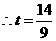 .
.
②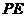 不能与
不能与 垂直.
垂直.
若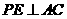 ,延长
,延长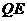 交
交 于
于 ,如图3,
,如图3,
则 .
.
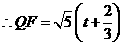 .
.
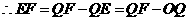

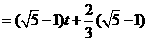 .
.
又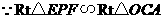 ,
,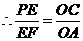 ,
,
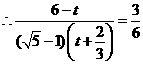 ,
,
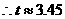 ,而
,而 ,
,
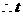 不存在.
不存在.
15. 解:(1)解法1:根据题意可得:A(-1,0),B(3,0);
则设抛物线的解析式为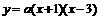 (a≠0)
(a≠0)
又点D(0,-3)在抛物线上,∴a(0+1)(0-3)=-3,解之得:a=1
∴y=x2-2x-3···································································································· 3分
自变量范围:-1≤x≤3···················································································· 4分
解法2:设抛物线的解析式为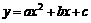 (a≠0)
(a≠0)
根据题意可知,A(-1,0),B(3,0),D(0,-3)三点都在抛物线上
∴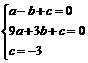 ,解之得:
,解之得: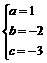
∴y=x2-2x-3··············································································· 3分
自变量范围:-1≤x≤3······························································ 4分
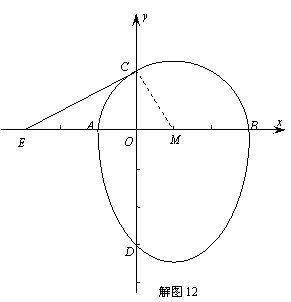
(2)设经过点C“蛋圆”的切线CE交x轴于点E,连结CM,
在Rt△MOC中,∵OM=1,CM=2,∴∠CMO=60°,OC=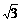
在Rt△MCE中,∵OC=2,∠CMO=60°,∴ME=4
∴点C、E的坐标分别为(0,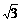 ),(-3,0) ·················································· 6分
),(-3,0) ·················································· 6分
 ∴切线CE的解析式为
∴切线CE的解析式为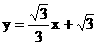 ··························································· 8分
··························································· 8分
(3)设过点D(0,-3),“蛋圆”切线的解析式为:y=kx-3(k≠0) ·························· 9分
由题意可知方程组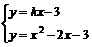 只有一组解
只有一组解
即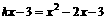 有两个相等实根,∴k=-2············································· 11分
有两个相等实根,∴k=-2············································· 11分
∴过点D“蛋圆”切线的解析式y=-2x-3····················································· 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com