
题目列表(包括答案和解析)
3、方差,标准差与极差。方差:顾名思义是“差的平方”,因有多个“差的平方”,所以要求平均数,弄清是“数据与平均数差的平方的平均数”,标准差是它的算术平方根。 会用计算器计算标准差与方差。
例6:数据90,91,92,93的标准差是( )
(A) (B) (C) (D)
 例7:甲、乙两人各射靶5次,已知甲所中环数是8、7、9、7、9,乙所中的环数的平均数x=8,方差S2乙=0.4,那么,对甲、乙的射击成绩的正确判断是( )
例7:甲、乙两人各射靶5次,已知甲所中环数是8、7、9、7、9,乙所中的环数的平均数x=8,方差S2乙=0.4,那么,对甲、乙的射击成绩的正确判断是( )
(A)甲的射击成绩较稳定 (B)乙的射击成绩较稳定
(C)甲、乙的射击成绩同样稳定 (D)甲、乙的射击成绩无法比较
例8:一个样本中,数据15和13各有4个,数据14有2个,求这个样本的平均数、方差、标准差和极差(标准差保留两个有效数字)
2、中位数,众数,平均数,加权平均数,注意区分这些概念。
相同点:都是为了描述一组数据的集中趋势的。
不同点:中位数--中间位置上的数据(当然要先按大小排列)
众数--出现的次数多的数据。
例3:某校篮球代表队中,5名队员的身高如下(单位:厘米):185,178,184,183,180,则这些队员的平均身高为( )
(A)183 (B)182 (C)181 (D)180
例4:已知一组数据为3,12,4,x,9,5,6,7,8的平均数为7,则x=
例5:某班第二组男生参加体育测试,引体向上成绩(单位:个)如下:
6 9 11 13 11 7 10 8 12
这组男生成绩的众数是____________,中位数是_________。
1、总体,个体,样本和样本容量。注意“考查对象”是所要研究的数据。
例1:为了了解某地区初一年级7000名学生的体重情况,从中抽取了500名学生的体重,就这个问题来说,下面说法中正确的是( )
(A)7000名学生是总体 (B)每个学生是个体
(C)500名学生是所抽取的一个样本 (D)样本容量是500
例2:某市今年有9068名初中毕业生参加升学考试,从中抽出300名考生的成绩进行分析。在这个问题中,总体是__________________________;个体是___ ________;样本是_______________________;样本容量是__________.
(二)不等式与不等式组 2不等式
3不等式(组)
1、几个概念:不等式(组)、不等式(组)的解集、解不等式(组)
2、不等式:
(1)怎样列不等式:
1.掌握表示不等关系的记号
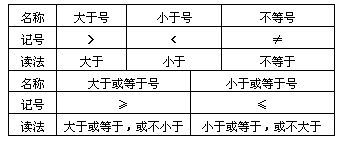
2.掌握有关概念的含义,并能翻译成式子.
(1)和、差、积、商、幂、倍、分等运算.
(2)“至少”、“最多”、“不超过”、“不少于”等词语.
例题:用不等式表示:
①a为非负数,a为正数,a不是正数
解:
②

(2)8与y的2倍的和是正数;
(3)x与5的和不小于0;
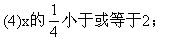
(5)x的4倍大于x的3倍与7的差;
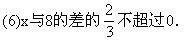
解:
(2)不等式的三个基本性质
不等式的性质1:如果a>b,那么a+c>b+c,a-c>b-c
推论:如果a+c>b,那么a>b-c。
不等式的性质2:如果a>b,并且c>0,那么ac>bc。
不等式的性质3:如果a>b,并且c<0,那么ac<bc。
(3) 解不等式的过程,就是要将不等式变形成x>a或x<a的形式
步骤:(与解一元一次方程类似)
去分母、去括号、移项、合并同类项、系数化一
(注:系数化一时,系数为正不等号方向不变;系数为负方向改变)
例题:①解不等式 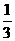 (1-2x)>
(1-2x)>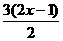
解:
②一本有300页的书,计划10天内读完,前五天因各种原因只读完100页.问从第六天起,每天至少读多少页?
解:
(4)在数轴上表示解集:“大右小左”“”
(5)写出下图所表示的不等式的解集
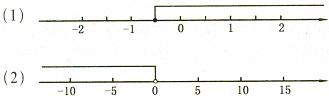
3、不等式组:求解集口诀:同大取大,同小取小,交叉中间,分开两边
例题:①
|
不等式组 |
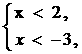 |
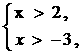 |
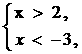 |
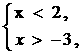 |
|
数轴表示 |
|
|
|
|
|
解集 |
|
|
|
|
②
例题:如果a>b,比较下列各式大小
(1)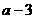
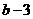 ,(2)
,(2)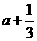
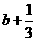 ,(3)
,(3)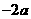
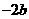
(4)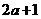
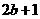 ,(5)
,(5)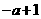
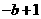
③
[05黄岗]不等式组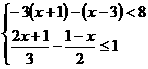 的解集应为( )
的解集应为( )
A、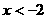 B、
B、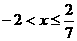 C、
C、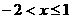 D、
D、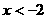 或
或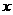 ≥1
≥1
解
④求不等式组2≤3x-7<8的整数解。
解:
课后练习:
1、下面方程或不等式的解法对不对?
(1)由-x=5,得x=-5;( )
(2)由-x>5,得x>-5;( )
(3)由2x>4,得x<-2;( )
(4)由-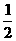 ≤3,得x≥-6。( )
≤3,得x≥-6。( )
2、判断下列不等式的变形是否正确:
(1)由a<b,得ac<bc;( )
(2)由x>y,且m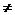 0,得-
0,得-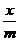 <
<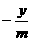 ;( )
;( )
(3)由x>y,得xz2 > yz2;( )
(4)由xz2 > yz2,得x>y;( )
3、把一堆苹果分给几个孩子,如果每人分3个,那么多8个;如果前面每人分5个,那么最后一人得到的苹果不足3个,问有几个孩子?有多少只苹果?
辅导班方程与不等式资料答案:
例题:.解方程:
(1)解:(x=1) (x=1)
(3)[05湘潭] 解: (m=4 )
例题:
①、解下列方程:
解: (1)( x1= 0 x2= 2 ) (2) (x1= 3√5 x2= -3√5 )
(3)(x1=0 x2= 2/3) (4)(x1= - 4 x2= 1)
(5)( t1= - 1 t2= 2 ) (6)(x1= - 4+3√2 x2= - 4-3√2 )
(7)(x1=(3+√15)/2 x2= ( 3-√15)/2 )
(8)(x1= 5 x2= 3/13)
② 填空:(1)x2+6x+( 9 )=(x+ 3 )2;
(2)x2-8x+(16)=(x-4 )2;
(3)x2+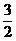 x+(9/16 )=(x+3/4 )2
x+(9/16 )=(x+3/4 )2
例题.①. ( C ) ② B ③.(A)
(4)根与系数的关系:x1+x2=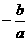 ,x1x2=
,x1x2=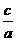
例题:( A )
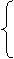 例题:[05泸州]解方程组
例题:[05泸州]解方程组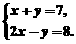 解得: x=5
解得: x=5
y=2
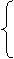 [05南京]解方程组
[05南京]解方程组 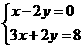 解得: x=2
解得: x=2
y=1
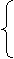 [05苏州]解方程组:
[05苏州]解方程组: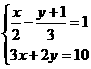 解得: x=3
解得: x=3
y=1/2
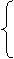 [05遂宁课改]解方程组:
[05遂宁课改]解方程组: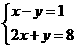 解得 : x=3
解得 : x=3
y=2
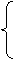 [05宁德]解方程组: 解得: x=3
[05宁德]解方程组: 解得: x=3
y=6
例题:①、解方程: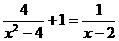 的解为 ( x= -1 )
的解为 ( x= -1 )
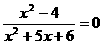 根为 (x= 2)
根为 (x= 2)
②、[北京市海淀区]( D )
(3)、( A )
例题:①解:设船在静水中速度为x千米/小时
依题意得:80/(x+3)= 60/(x-3) 解得:x=21 答:(略)
②解:设乙车速度为x千米/小时,则甲车的速度为(x+10)千米/小时
依题意得:450/(x+10)=400/x
解得x=80 x+1=90 答:(略)
③解:设原零售价为a元,每次降价率为x
依题意得:a(1-x )²=a/2 解得:x≈0.292 答:(略)
④[05绵阳]解:A=6/5 B= -4/5
⑤解:A
⑥解:三个连续奇数依次为x-2、x、x+2
依题意得:(x-2)² + x² +(x+2)² =371 解得:x=±11
当x=11时,三个数为9、11、13;
当x= -11时,三个数为 -13、-11、-9 答(略)
⑦解:设小正方形的边长为x cm依题意:(60-2x)(40-2x)=800 解得x1=40 (不合题意舍去)
x2=10 答(略)
例题:用不等式表示:①a为非负数,a为正数,a不是正数
解: a≥0 a﹥0 a≤0
② 解:(1)2x/3 -5<1 (2)8+2y>0 (3)x+5≥0
(4)x/4 ≤2 (5)4x>3x-7 (6)2(x-8)/ 3 ≤ 0
例题:①解不等式 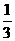 (1-2x)>
(1-2x)>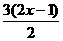
解得:x<1/2
②解:设每天至少读x页
依题意(10-5)x + 100 ≥ 300 解得x≥40 答(略)
(6)写出下图所表示的不等式的解集
 x≥ -1/2
x≥ -1/2
x<0
例题:① ②
例题:如果a>b,比较下列各式大小
(1)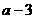 >
>
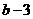 ,(2)
,(2)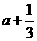 >
> 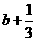 ,(3)
,(3)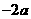 <
<
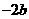
(4)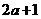 >
> 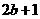 ,(5)
,(5)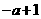 <
<
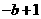
③[05黄岗]( C )
④求不等式组2≤3x-7<8的整数解。解得:3≤x<5
课后练习:
1、下面方程或不等式的解法对不对?
(5)由-x=5,得x=-5;( 对 )
(6)由-x>5,得x>-5;(错 )
(7)由2x>4,得x<-2;( 错 )
(8)由-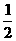 x≤3,得x≥-6。(对 )
x≤3,得x≥-6。(对 )
2、判断下列不等式的变形是否正确:
(5)由a<b,得ac<bc;( 错 )
(6)由x>y,且m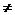 0,得-
0,得-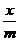 <
<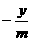 ;( 错 )
;( 错 )
(7)由x>y,得xz2 > yz2;( 错 )
(8)由xz2 > yz2,得x>y;(对 )
3、把一堆苹果分给几个孩子,如果每人分3个,那么多8个;如果前面每人分5个,那么最后一人得到的苹果不足3个,问有几个孩子?有多少只苹果?
解:设有x个孩,依题意:3x+8 - 5(x-1)<3 解得5<x≤6.5
X=6 答(略)
(一)方程与方程组 3一元二次方程
4方程组
5分式方程
6应用
1、 概念:方程、方程的解、解方程、方程组、方程组的解
2、 一元一次方程:
解方程的步骤:去分母、去括号、移项、合并同类项、系数化一(未知项系数不能为零)
例题:.解方程:
(1) 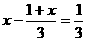 (2)
(2)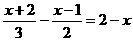
解:
(3)[05湘潭] 关于x的方程mx+4=3x+5的解是x=1,则m= 。
解:
3、一元二次方程:
(1)
一般形式: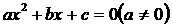
(2) 解法:
直接开平方法、因式分解法、配方法、公式法
求根公式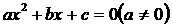
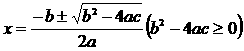
例题:
①、解下列方程:
(1)x2-2x=0; (2)45-x2=0;
(3)(1-3x)2=1; (4)(2x+3)2-25=0.
(5)(t-2)(t+1)=0; (6)x2+8x-2=0
(7 )2x2-6x-3=0; (8)3(x-5)2=2(5-x)
解:
② 填空:
(1)x2+6x+( )=(x+ )2;
(2)x2-8x+( )=(x- )2;
(3)x2+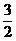 x+( )=(x+ )2
x+( )=(x+ )2
(3)判别式△=b²-4ac的三种情况与根的关系
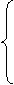
 当
当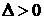 时
有两个不相等的实数根 ,
时
有两个不相等的实数根 ,
 当
当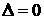 时
有两个相等的实数根
时
有两个相等的实数根
 当
当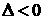 时
没有实数根。
时
没有实数根。
 当△≥0时 有两个实数根
当△≥0时 有两个实数根
例题.①.(无锡市)若关于x的方程x2+2x+k=0有两个相等的实数根,则k满足 ( )
A.k>1 B.k≥1 C.k=1 D.k<1
②(常州市)关于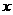 的一元二次方程
的一元二次方程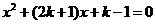 根的情况是( )
根的情况是( )
(A)有两个不相等实数根 (B)有两个相等实数根
(C)没有实数根 (D)根的情况无法判定
③.(浙江富阳市)已知方程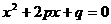 有两个不相等的实数根,则
有两个不相等的实数根,则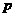 、
、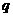 满足的关系式是( )
满足的关系式是( )
A、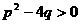 B、
B、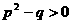 C、
C、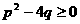 D、
D、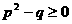
(4)根与系数的关系:x1+x2=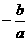 ,x1x2=
,x1x2=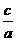
例题: (浙江富阳市)已知方程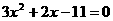 的两根分别为
的两根分别为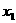 、
、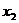 ,则
,则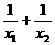 的值是( )
的值是( )
A、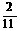 B、
B、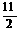 C、
C、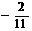 D、
D、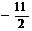
4、 方程组:
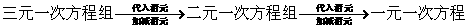
二元(三元)一次方程组的解法:代入消元、加减消元
例题:[05泸州]解方程组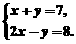
解
[05南京]解方程组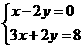
解
[05苏州]解方程组: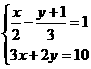
解
[05遂宁课改]解方程组: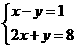
解
[05宁德]解方程组:
解
5、分式方程:
分式方程的解法步骤:
(1) 一般方法:选择最简公分母、去分母、解整式方程,检验
(2) 换元法
例题:①、解方程: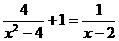 的解为
的解为
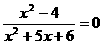 根为
根为
②、[北京市海淀区]当使用换元法解方程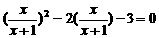 时,若设
时,若设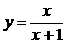 ,则原方程可变形为( )
,则原方程可变形为( )
A.y2+2y+3=0 B.y2-2y+3=0
C.y2+2y-3=0 D.y2-2y-3=0
(3)、用换元法解方程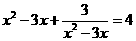 时,设
时,设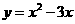 ,则原方程可化为( )
,则原方程可化为( )
(A)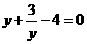 (B)
(B)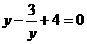 (C)
(C)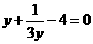 (D)
(D)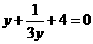
6、应用:
(1)分式方程(行程、工作问题、顺逆流问题)
(2)一元二次方程(增长率、面积问题)
(3)方程组实际中的运用
例题:①轮船在顺水中航行80千米所需的时间和逆水航行60千米所需的时间相同.已知水流的速度是3千米/时,求轮船在静水中的速度.(提示:顺水速度=静水速度+水流速度,逆水速度=静水速度-水流速度)
解:
②乙两辆汽车同时分别从A、B两城沿同一条高速公路驶向C城.已知A、C两城的距离为450千米,B、C两城的距离为400千米,甲车比乙车的速度快10
千米/时,结果两辆车同时到达C城.求两车的速度
解
③某药品经两次降价,零售价降为原来的一半.已知两次降价的百分率一样,求每次降价的百分率.(精确到0.1%)
解
④[05绵阳]已知等式 (2A-7B) x+(3A-8B)=8x+10对一切实数x都成立,求A、B的值
解
⑤[05南通]某校初三(2)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:
|
捐款(元) |
1 |
|
3 |
4 |
||
|
人 数 |
6 |
|
|
7 |
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.
若设捐款2元的有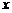 名同学,捐款3元的有
名同学,捐款3元的有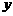 名同学,根据题意,可得方程组
名同学,根据题意,可得方程组
A、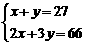 B、
B、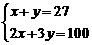 C、
C、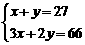 D、
D、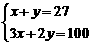
解
⑥已知三个连续奇数的平方和是371,求这三个奇数.
解
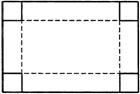 ⑦一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方米.求截去正方形的边长.
⑦一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方米.求截去正方形的边长.
解:
1几个概念
 知识结构及内容:
1几个概念
知识结构及内容:
1几个概念
2一元一次方程
43. 解:(1)设生产 型桌椅
型桌椅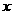 套,则生产
套,则生产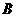 型桌椅
型桌椅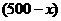 套,由题意得
套,由题意得
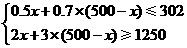
解得
因为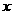 是整数,所以有11种生产方案.
是整数,所以有11种生产方案.
(2)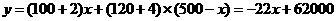
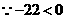 ,
,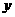 随
随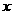 的增大而减少.
的增大而减少.
 当
当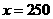 时,
时,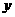 有最小值.
有最小值.
 当生产
当生产 型桌椅250套、
型桌椅250套、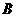 型桌椅250套时,总费用最少.
型桌椅250套时,总费用最少.
此时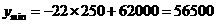 (元)
(元)
(3)有剩余木料,最多还可以解决8名同学的桌椅问题.
42. 解:由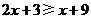 ,得
,得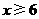
由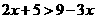 ,得
,得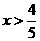
所以,不等式组的解集是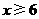
41. 解:(1)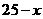 ;
;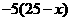
(2)根据题意,得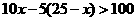
解得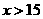
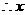 的最小正整数解是
的最小正整数解是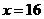
答:小明同学至少答对16道题.
40. 解:3x-2<7
3x<7+2
3x<9
x<3
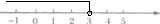
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com