
题目列表(包括答案和解析)
19. 解:解不等式①,得x<2, …………………………………………………2分
解不等式②,得x≥-1. ………………………………………………4分
所以,不等式组的解集是-1≤x<2. ……………………………………5分
不等式组的解集在数轴上表示如下:

………………………………………………………………………………6分
18. 解不等式① 得x < 1 ················ 2分
解不等式② 得x > -1 ················· 4分
 所以这个不等式组的解集为:-1<x<1 ················ 6分
所以这个不等式组的解集为:-1<x<1 ················ 6分
17. 解:(1)由题得到:2.2x+2.1y+2(30-x-y)=64 所以 y = -2x+40
又x≥4,y≥4,30-x-y≥4,得到14≤x≤18
(2)Q=6x+8y+5(30-x-y)= -5x+170
Q随着x的减小而增大,又14≤x≤18,所以当x=14时,Q取得最大值,
即Q= -5x+170=100(百元)=1万元.
因此,当x=14时,y = -2x+40=12, 30-x-y=4
所以,应这样安排:A种水果用14辆车,B种水果用12辆车,C种水果用4辆车
16. 解:原不等式组的解集是: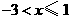 ,
,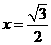 满足该不等式组.
满足该不等式组.
15. 解:(1)解:由题意:
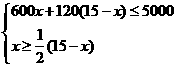 ,………………2分
,………………2分
解得:5≤x≤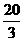 ………………3分
………………3分
∵x为整数,∴x=5,6 ………………4分
∴共两种购票方案:
方案一:A种船票5张,B种船票10张
方案二:A种船票6张,B种船票9张 ………………5分
(2)因为B种船票价格便宜,因此B种船票越多,总购票费用少.
∴第一种方案省钱,为5×600+120×10=4200(元)………………8分
前两年第20题知识点分布:2006年考查内容不等式组设计方案,2007年考查内容不等式组设计方案
14. 解:(1)设租用一辆甲型汽车的费用是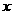 元,租用一辆乙型汽车的费用是
元,租用一辆乙型汽车的费用是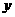 元.
元.
由题意得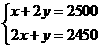 ··························· 2分
··························· 2分
解得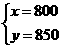 ······························· 1分
······························· 1分
答:租用一辆甲型汽车的费用是800元,租用一辆乙型汽车的费用是850元.
(2)设租用甲型汽车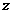 辆,则租用乙型汽车
辆,则租用乙型汽车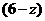 辆.
辆.
由题意得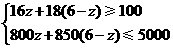 ····················· 2分
····················· 2分
解得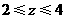 ······························· 1分
······························· 1分
由题意知,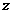 为整数,
为整数,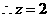 或
或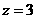 或
或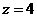
 共有3种方案,分别是:
共有3种方案,分别是:
方案一:租用甲型汽车2辆,租用乙型汽车4辆;
方案二:租用甲型汽车3辆,租用乙型汽车3辆;
方案三:租用甲型汽车4辆,租用乙型汽车2辆.················ 1分
方案一的费用是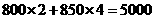 (元);
(元);
方案二的费用是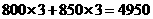 (元);
(元);
方案三的费用是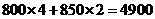 (元)
(元)
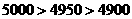 ,所以最低运费是4900元.················ 1分
,所以最低运费是4900元.················ 1分
答:共有3种方案,分别是:方案一:租用甲型汽车2辆,租用乙型汽车4辆;
方案二:租用甲型汽车3辆,租用乙型汽车3辆;
方案三:租用甲型汽车4辆,租用乙型汽车2辆.
最低运费是4900元.
13. 解:(1)设预定男篮门票x张,则乒乓球门票(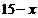 )张.得:1000x+500(15-x)=12000,解得:x = 9 ∴
)张.得:1000x+500(15-x)=12000,解得:x = 9 ∴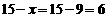
(2)设足球门票与乒乓球门票数都预定y张,则男篮门票数为(15-2y)张,得: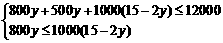 ,
,
解得: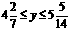 .由y为正整数可得y=5. 15-2y=5
.由y为正整数可得y=5. 15-2y=5
答:(1)略 (2)略
12. 解: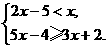
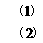
由不等式(1)得: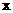 <5
<5
由不等式(2)得: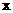 ≥3
≥3
所以:5>x≥3
11. 解:(2)5x+3x<1+3
8x<4
x<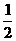
10. 解:(1)1或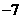 .··························· 3分
.··························· 3分
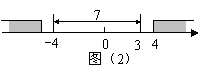 (2)
(2)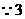 和
和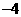 的距离为7,
的距离为7,
因此,满足不等式的解对应的点3与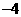 的两侧.
的两侧.
当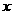 在3的右边时,如图(2),
在3的右边时,如图(2),
易知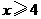 .················ 5分
.················ 5分
当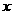 在
在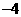 的左边时,如图(2),
的左边时,如图(2),
易知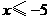 .··············· 7分
.··············· 7分
 原不等式的解为
原不等式的解为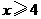 或
或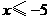 ······················ 8分
······················ 8分
(3)原问题转化为:
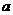 大于或等于
大于或等于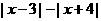 最大值.··········· 9分
最大值.··········· 9分
当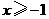 时,
时,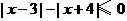 ,
,
当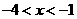 ,
,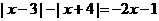 随
随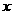 的增大而减小,
的增大而减小,
当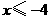 时,
时,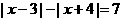 ,
,
即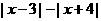 的最大值为7.······················ 11分
的最大值为7.······················ 11分
故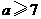 . 12分
. 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com