
题目列表(包括答案和解析)
23.(天津市2008年)已知抛物线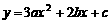 ,
,
(Ⅰ)若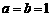 ,
,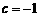 ,求该抛物线与
,求该抛物线与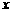 轴公共点的坐标;
轴公共点的坐标;
(Ⅱ)若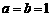 ,且当
,且当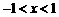 时,抛物线与
时,抛物线与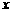 轴有且只有一个公共点,求
轴有且只有一个公共点,求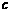 的取值范围;
的取值范围;
(Ⅲ)若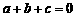 ,且
,且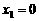 时,对应的
时,对应的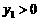 ;
;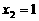 时,对应的
时,对应的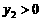 ,试判断当
,试判断当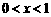 时,抛物线与
时,抛物线与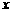 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
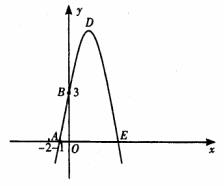
22.(2008年四川省宜宾市)已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.
(1)求该抛物线的解析式;
(2)若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积;
(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
(注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为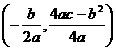 )
)
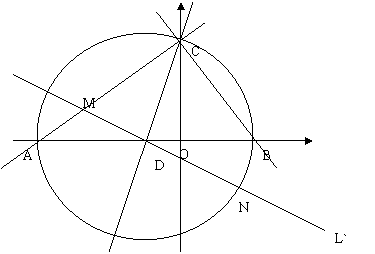
21.(2008年乐山市)在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆过点C若C的坐标为(0,2),AB=5, A,B两点的横坐标XA,XB是关于X的方程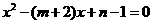 的两根:
的两根:
(1) 求m,n的值
(2)
若∠ACB的平分线所在的直线 交x轴于点D,试求直线
交x轴于点D,试求直线 对应的一次函数的解析式
对应的一次函数的解析式
(3)
过点D任作一直线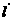 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则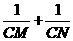 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由

20.(2008年成都市)如图,在平面直角坐标系xOy中,△OAB的顶点A的坐标为(10,0),顶点B在第一象限内,且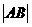 =3
=3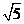 ,sin∠OAB=
,sin∠OAB=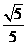 .
.
(1)若点C是点B关于x轴的对称点,求经过O、C、A三点的抛物线的函数表达式;
(2)在(1)中,抛物线上是否存在一点P,使以P、O、C、A为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若将点O、点A分别变换为点Q( -2k ,0)、点R(5k,0)(k>1的常数),设过Q、R两点,且以QR的垂直平分线为对称轴的抛物线与y轴的交点为N,其顶点为M,记△QNM的面积为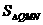 ,△QNR的面积
,△QNR的面积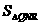 ,求
,求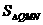 ∶
∶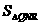 的值.
的值.
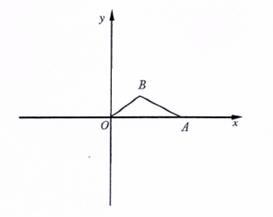
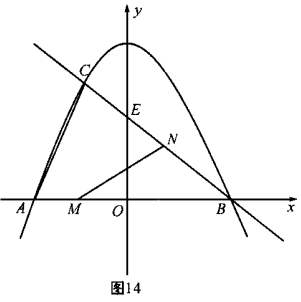
19.(2008年四川省巴中市) 已知:如图14,抛物线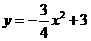 与
与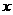 轴交于点
轴交于点 ,点
,点 ,与直线
,与直线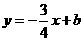 相交于点
相交于点 ,点
,点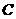 ,直线
,直线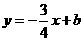 与
与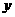 轴交于点
轴交于点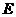 .
.
(1)写出直线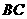 的解析式.
的解析式.
(2)求 的面积.
的面积.
(3)若点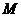 在线段
在线段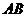 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从 向
向 运动(不与
运动(不与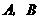 重合),同时,点
重合),同时,点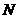 在射线
在射线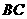 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从 向
向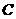 运动.设运动时间为
运动.设运动时间为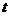 秒,请写出
秒,请写出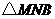 的面积
的面积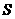 与
与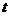 的函数关系式,并求出点
的函数关系式,并求出点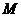 运动多少时间时,
运动多少时间时,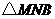 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
18.(2008年沈阳市)如图所示,在平面直角坐标系中,矩形 的边
的边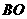 在
在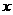 轴的负半轴上,边
轴的负半轴上,边 在
在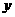 轴的正半轴上,且
轴的正半轴上,且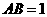 ,
,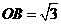 ,矩形
,矩形 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转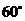 后得到矩形
后得到矩形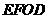 .点
.点 的对应点为点
的对应点为点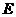 ,点
,点 的对应点为点
的对应点为点 ,点
,点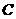 的对应点为点
的对应点为点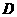 ,抛物线
,抛物线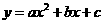 过点
过点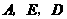 .
.
(1)判断点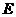 是否在
是否在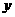 轴上,并说明理由;
轴上,并说明理由;
(2)求抛物线的函数表达式;
(3)在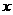 轴的上方是否存在点
轴的上方是否存在点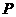 ,点
,点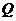 ,使以点
,使以点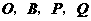 为顶点的平行四边形的面积是矩形
为顶点的平行四边形的面积是矩形 面积的2倍,且点
面积的2倍,且点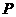 在抛物线上,若存在,请求出点
在抛物线上,若存在,请求出点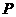 ,点
,点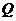 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

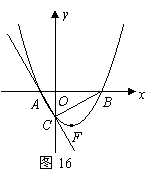
17.(2008年辽宁省十二市)如图16,在平面直角坐标系中,直线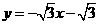 与
与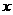 轴交于点
轴交于点 ,与
,与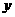 轴交于点
轴交于点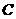 ,抛物线
,抛物线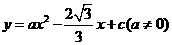 经过
经过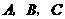 三点.
三点.
(1)求过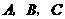 三点抛物线的解析式并求出顶点
三点抛物线的解析式并求出顶点 的坐标;
的坐标;
(2)在抛物线上是否存在点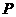 ,使
,使 为直角三角形,若存在,直接写出
为直角三角形,若存在,直接写出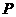 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由;
(3)试探究在直线 上是否存在一点
上是否存在一点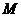 ,使得
,使得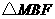 的周长最小,若存在,求出
的周长最小,若存在,求出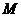 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

16.(2008年浙江省绍兴市)将一矩形纸片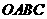 放在平面直角坐标系中,
放在平面直角坐标系中,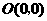 ,
,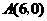 ,
,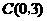 .动点
.动点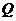 从点
从点 出发以每秒1个单位长的速度沿
出发以每秒1个单位长的速度沿 向终点
向终点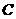 运动,运动
运动,运动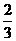 秒时,动点
秒时,动点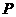 从点
从点 出发以相等的速度沿
出发以相等的速度沿 向终点
向终点 运动.当其中一点到达终点时,另一点也停止运动.设点
运动.当其中一点到达终点时,另一点也停止运动.设点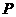 的运动时间为
的运动时间为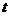 (秒).
(秒).
(1)用含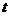 的代数式表示
的代数式表示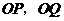 ;
;
(2)当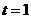 时,如图1,将
时,如图1,将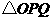 沿
沿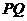 翻折,点
翻折,点 恰好落在
恰好落在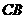 边上的点
边上的点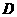 处,求点
处,求点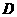 的坐标;
的坐标;
(4)
连结 ,将
,将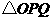 沿
沿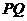 翻折,得到
翻折,得到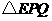 ,如图2.问:
,如图2.问: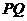 与
与 能否平行?
能否平行?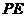 与
与
能否垂直?若能,求出相应的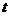 值;若不能,说明理由.
值;若不能,说明理由.


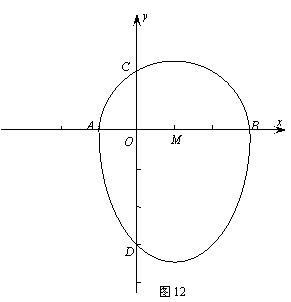
15.(2008湖南益阳)我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.
如图12,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
(1) 请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围;
(2)你能求出经过点C的“蛋圆”切线的解析式吗?试试看;
(3)开动脑筋想一想,相信你能求出经过点D的“蛋圆”切线的解析式.
14.(2008山东威海)如图,点A(m,m+1),B(m+3,m-1)都在反比例函数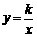 的图象上.
的图象上.
 (1)求m,k的值;
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点,
以点A,B,M,N为顶点的四边形是平行四边形,
 试求直线MN的函数表达式.
试求直线MN的函数表达式.
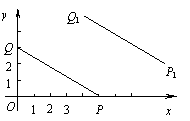 (3)选做题:在平面直角坐标系中,点P的坐标
(3)选做题:在平面直角坐标系中,点P的坐标
为(5,0),点Q的坐标为(0,3),把线段PQ向右平
移4个单位,然后再向上平移2个单位,得到线段P1Q1,
则点P1的坐标为 ,点Q1的坐标为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com