
题目列表(包括答案和解析)
4. 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
探究:
(1)如图甲,已知△ABC中∠C=900,你能把△ABC分割成2个与它自己相似的
小直角三角形吗?若能,请在图甲中画出分割线,并说明理由.
答:
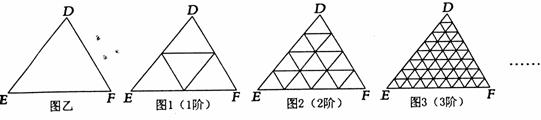
(2)一般地,“任意三角形都是自相似图形”,只要顺次连结三角形各边中点,则可将原三角形分割为四个都与它自己相似的小三角形.我们把△DEF(图乙)第一次顺次连结各边中点所进行的分割,称为1阶分割(如图1);把1阶分割得出的4个三角形再分别顺次连结它的各边中点所进行的分割,称为2阶分割(如图2)…依次规则操作下去.n阶分割后得到的每一个小三角形都是全等三角形(n为正整数),设此时小三角形的面积为SN.
①若△DEF的面积为10000,当n为何值时,2<Sn<3?(请用计算器进行探索,要求至少写出三次的尝试估算过程)
②当n>1时,请写出一个反映Sn-1,Sn,Sn+1之间关系的等式(不必证明)
3.小明受《乌鸦喝水》故事的启发,利用量桶和体积相同的小球进行了如下操作:

请根据图中给出的信息,解答下列问题:
(1)放入一个小球量桶中水面升高___________ ;
;
(2)求放入小球后量桶中水面的高度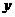 (
( )与小球个数
)与小球个数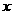 (个)之间的一次函数关系式(不要求写出自变量的取值范围);
(个)之间的一次函数关系式(不要求写出自变量的取值范围);
(3)量桶中至少放入几个小球时有水溢出?
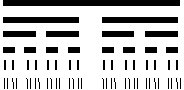
2. 1883年,康托尔构造的这个分形,称做康托尔集.从数轴上单位长度线段开始,康托尔取走其中间三分之一而达到第一阶段;然后从每一个余下的三分之一线段中取走其中间三分之一而达到第二阶段.无限地重复这一过程,余下的无穷点集就称做康托尔集.上图是康托尔集的最初几个阶段,当达到第八个阶段时,余下的所有线段的长度之和为( )

A.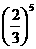 B.
B.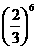 C.
C.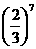 D.
D.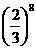
1.我国《劳动法》对劳动者的加班工资作出了明确规定,“五一”长假期间,前3天是法定休假日,用人单位应按照不低于劳动者本人日工资或小时工资300%支付加班工资,后4天是休息日,用人单位应首先安排劳动者补休,不能安排补休的,按照不低于劳动本人日工资或小时工资的200%支付加班工资.小朱由于工作需要,今年5月2日、3日、4日共加班三天,已知小朱的日工资标准为47元,则小朱“五一”长假加班三天的加班工资应不低于______________元.
3.图表分析法
例1某服装厂现有A种布料70m,B种布料52m,现计划用这两种布料生产M、N两种型号的时装80套。已知做一套M型号的时装需要A种布料0.6m,B种布料0.9m,可获利45元,做一套N型号的时装需要A种布料1.1m,B种布料0.4m,可获利50元。若设生产N型号的时装套数为x,用这批布料生产这两种型号的时装所获的总利润为y元。(1)求y与x的函数关系式,并求出自变量x的取值范围;(2)该服装厂在生产这批时装中,当生产N型号的时装多少套时,所获利润最大?最大利润是多少?
解析:虽然题目看起来与前面的调运问题联系不大,但这道题中同样也出现了较多量及数据,因而同样可利用图表来整理数据,而且也方便易行。对于第一个问题的函数关系,根据题中已设好的未知数及相关条件易得“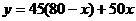 ”,化简即“
”,化简即“ ”。这道题的难点在于确定自变量x的取值范围,对于这个问题,可用两种方法进行分析。
”。这道题的难点在于确定自变量x的取值范围,对于这个问题,可用两种方法进行分析。
分析方法一:列表法
|
每套时装用料 |
(80-x)套 M型时装 |
x套 N型时装 |
总用料量 |
|
A种布料(共70m) |
0.6 |
1.1 |
0.6(80-x)+1.1x |
|
B种布料(共52m) |
0.9 |
0.4 |
0.9(80-x)+0.4x |
上表格形式简单,内容清晰,完成表格并不困难,重要的是让学生理解求x范围的关键在于两种型号的时装每种布料用量和不能超过所提供的布料,由此得出两个不等式“0.6(80-x)+1.1x≤70,0.9(80-x)+0.4x≤52”。解两个不等式即可求出x的取值范围为“40≤x≤44”。其实到这里问题也就基本解决了,因为第二个问题可由刚才的结论直接求得。





和例1相比,这个示意图在结构上更为简洁,每种型号的时装都用到两种布料,图中箭头指向是该布料的使用情况,如:由A种布料引出的两根箭头表示A种布料分别用于M型时装每套0.6m,用于N型时装每套1.1m,而M型时装共生产(80-x)套,这样A种布料一共使用了[0.6(80-x)+1.1x]m,同理可得,B种布料一共用了[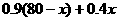 ]m。通过这个示意图也很容易求出x的取值范围。具体解题过程如下:
]m。通过这个示意图也很容易求出x的取值范围。具体解题过程如下:
答案:(1)由题意得 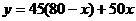
化简可得 
又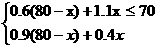
解之得 40≤x≤44
(2)当x=44时,y=5×44+3600=3820
∴当生产N型号的时装44套时,所获利润最大,最大利润是3820元。
方法点拨:通过图表将题目中的各数据间的关系更为简洁的体现出来,使得题意更加明朗,各个量之间的关系也变得国家更加清晰,从而降低了解题的难度。再结合问题,设出未知数后,利用图表所反映出来的关系,可以把各个相关量全部表示出来,最后根据相等关系,不难列出方程,完成解题。
●拓展演练
2.直观作图法
例1操作与探究:
(1)图①是一块直角三角形纸片.将该三角形纸片按如图方法折叠,是点A与点C重合,DE为折痕.试证明△CBE等腰三角形;
(2)再将图①中的△CBE沿对称轴EF折叠(如图②).通过折叠,原三角形恰好折成两个重合的矩形,其中一个是内接矩形,另一个是拼合(指无缝无重叠)所成的矩形,我们称这样的两个矩形为“组合矩形”.你能将图③中的△ABC折叠成一个组合矩形吗?如果能折成,请在图③中画出折痕;
(3)请你在图④的方格纸中画出一个斜三角形,同时满足下列条件:①折成的组合矩形为正方形;②顶点都在格点(各小正方形的顶点)上;
(4)有一些特殊的四边形,如菱形,通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上).请你进一步探究,一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足何条件是,一定能折成组合矩形?

解析:(1)∵∠ECB=90°-∠DCE,∠B=90°-∠A,又由对称性知,∠A=∠DCE,∴∠ECB=∠B,∴△BCE是等腰三角形.

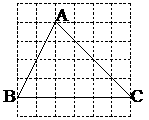
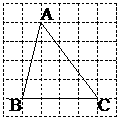
图1 图2
图10-13
(2)如图10-13中的图1所示(共有三种折法,折痕画对均可)
(3)如图10-13中的图2所示(答案不唯一,只要体现出一条边与该边上的高相等即可)
(4)当一个四边形的两条对角线互相垂直时,可以折成一个组合矩形.
答案:略(见解析)
方法点拨:本题要求首先要能正确理解题中所介绍的“组合矩形”的概念,同时能熟练运用从特殊到一般的学习方法,由题目的已知图示,完成一般情形下的相关操作.
解题关键:要能拼合(即无缝无重叠),根据(1)问的证明,第一次折叠时必须沿其中一条中位线,然后再沿着与这条中位线平行的边的垂直方向进行折叠即可.
1.实践操作法
例1印刷一本书,为了使装订成书后页码恰好为连续的自然数,可按如下方法操作:如图10-8,先将一张整版的纸,对折一次为4页,再对折一次为8页,连续对折三次为16页,……;然后再排页码. 如果想设计一本16页的毕业纪念册,请你按图1、图2、图3(图中的1,16表示页码)的方法折叠,在图4中填上按这种折叠方法得到的各页在该面相应位置上的页码.
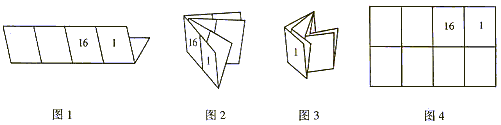
图10-8
解析:本题单凭想象完成有一定困难,但其实际操作较为简单,通过实际操作容易得到答案.
答案:
|
8 |
9 |
16 |
1 |
|
5 |
12 |
13 |
4 |
方法点拨:在考试时,完成这道题单凭想象完成比较困难,但却操作简单易行,建议考试时遇这类问题时,可进行实际操作.
3.举一反三法
 例4如图10-6,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )
例4如图10-6,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )
A.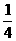 cm2 B.
cm2 B. cm2
cm2
C.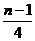 cm2 D.
cm2 D.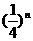 cm2
cm2
解析:通过观察,不难发现,每两个连续的这样摆放的正方形中互相重叠的部分的面积刚好是一个正方形面积的四分之一,而三个连续这样摆放的正方形有两个这样的重叠的部分.所以n个这样的正方形重叠部分的面积和为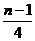 cm2
cm2
答案:选择C
方法点拨:归纳猜想题中,有许多试题是通过局部反映整体的.这时,要求能通过观察,发现这种特点,然后只需分析或者解决其中部分问题,再通过举一反三,达到通盘解决问题的目标.利用旋转或三角形全等知识可证明每两个相邻正方形重叠部分的面积等于一个正方形面积的四分之一,再通过观察,发现后面全部具有相同的规律,容易求出结果.
2.数形结合法
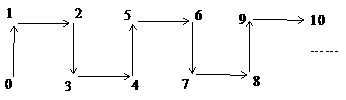
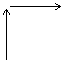
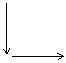
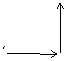
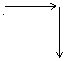
例2探索规律:根据图10-4中箭头指向的规律,从2004到2005再到2006,箭头的方向是( )
A B C D
图10-4
解析:仔细观察分析,本题是通过图形的方式反映数字重复出现的规律,通过观察,可以看出,每隔4个数是一个循环,从图形上体现出相同的规律,并且4既是终了位置同时又是下一个新的循环的起始位置.要找出2004至2005再到2006的箭头方向,计算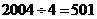 ,说明第2004个数刚好是完成第501个循环,同时又将开始下一个循环.
,说明第2004个数刚好是完成第501个循环,同时又将开始下一个循环.
答案:A
方法点拨:在许多数学试题中,数形结合思想至关重要,在归纳猜想题里也不例外.有时单从数字中很难看出什么眉目,但如果能有意识的从“形”的角度联系起来进行分析,往往会收到出奇制胜的效果.本题是数形结合反映规律,重复出现的图形反映出数字所具有的规律,要求解数字问题,关键还在于找出图形体现出的规律.
例3如图10-5,已知矩形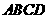 的边长
的边长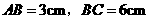 .某一时刻,动点
.某一时刻,动点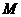 从
从 点出发沿
点出发沿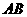 方向以
方向以 的速度向
的速度向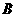 点匀速运动;同时,动点
点匀速运动;同时,动点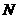 从
从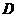 点出发沿
点出发沿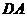 方向以
方向以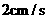 的速度向
的速度向 点匀速运动,问:
点匀速运动,问:
(1)经过多少时间, 的面积等于矩形
的面积等于矩形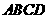 面积的
面积的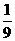 ?
?
(2)是否存在时刻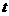 ,使以
,使以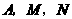 为顶点的三角形与
为顶点的三角形与 相似?若存在,求
相似?若存在,求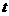 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.


解析:(1)设经过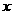 秒后,
秒后, 的面积等于矩形
的面积等于矩形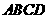 面积的
面积的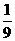 ,
,
则有: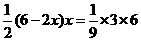 ,即
,即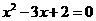 ,
,
解方程,得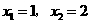 .
.
经检验,可知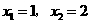 符合题意,所以经过1秒或2秒后,
符合题意,所以经过1秒或2秒后, 的面积等于矩形
的面积等于矩形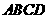 面积的
面积的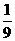 .
.
(2)假设经过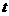 秒时,以
秒时,以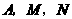 为顶点的三角形与
为顶点的三角形与 相似,
相似,
由矩形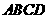 ,可得
,可得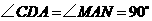 ,因此有
,因此有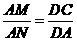 或
或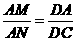
即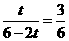 ①,或
①,或 ②.
②.
解①,得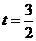 ;解②,得
;解②,得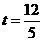
经检验,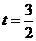 或
或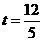 都符合题意,所以动点
都符合题意,所以动点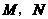 同时出发后,经过
同时出发后,经过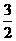 秒或
秒或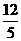 秒时,以
秒时,以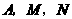 为顶点的三角形与
为顶点的三角形与 相似
相似
答案:(1)经过1秒或2秒后;(2),经过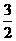 秒或
秒或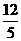 秒时.
秒时.
方法点拨:通过动点问题考查一元二次方程(二次函数)是数学建模的一种常见形式.这也是一种数形结合问题,几何图形中的点的运动情形可以通过代数式来体现,从形的角度无法解决的问题,从“数”的角度求解却显得很容易.(1)本题中矩形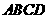 面积已知,故解题关键在于找出
面积已知,故解题关键在于找出 的底与高,通过设定经过的时间为未知数,把
的底与高,通过设定经过的时间为未知数,把 面积用含未知数的式子表示出来,然后解方程即可.(2)利用相似得到比例式,从而得到相关方程并求解.
面积用含未知数的式子表示出来,然后解方程即可.(2)利用相似得到比例式,从而得到相关方程并求解.
1.循序渐进法
例1如图10-3,是五角星灯连续旋转闪烁所成的三个图形.照此规律闪烁,下一个呈现出来的图形是( )


A B C D
解析:观察上面三个正方形,可以看出每个五角星中有三个深色的三角形,其中一个单独的与另两个相邻的三角形相对,闪烁一次,三个深色三角形作为一个整体,可看作是顺时针旋转144度(也就是与原来的隔一角).按此规律,容易找出下一次闪烁后呈现出来的图形.
答案:A
方法点拨:归纳猜想题最忌讳毫无章法,胡乱猜测,归纳猜想题往往是有章可循的,只要你循序渐进,仔细观察和分析,一定可以从题目的条件中发现重要信息,从而实现轻松解题.本题要求从现有的三个图形中,找出规律,然后分析出再一次闪烁后出现的图形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com