
题目列表(包括答案和解析)
1.(2008巴中市)在常温下向一定量的水中加入食盐Nacl,则能表示盐水溶液的浓度与加入的Nacl的量之间的变化关系的图象大致是( )
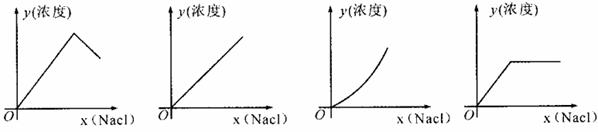
A B C D
2.、(2008泰州市)根据流程右边图中的程序,当输入数值x为-2时,输出数值y为B
A.4 B.6 C.8 D.10
考点四 函数的图象.
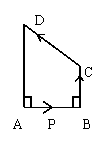
 例题(2008四川省自贡市)如图,在四边形ABCD中,动点P从点A开始沿
例题(2008四川省自贡市)如图,在四边形ABCD中,动点P从点A开始沿
的路径匀速前进到D为止。在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( )

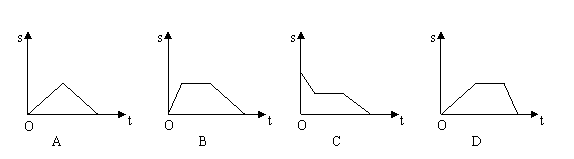
 思路点拨:对于函数图象类问题,主要是反映自变量与函数值之间的变化规律,因此抓住自变量的变化所产生的函数值是如何变化的,就容易排除干扰选项而得出答案.
思路点拨:对于函数图象类问题,主要是反映自变量与函数值之间的变化规律,因此抓住自变量的变化所产生的函数值是如何变化的,就容易排除干扰选项而得出答案.
解析:根据动点的移动知,P点在AB上移动时,△APD的面积S是在增加,排除答案
C ,P点在BC上移动时,△APD的面积S是不变化的,排除答案A ,因为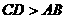 ,点P是匀速前进,所以在CD上移动的时间比在AB上移动所用时间多,所以排除答案D
,点P是匀速前进,所以在CD上移动的时间比在AB上移动所用时间多,所以排除答案D
,选B
规律总结:要注意弄清楚点的移动与图象的对应关系,特别注意抓特殊点,特殊线段.
[针对训练]
2.(2008齐齐哈尔)函数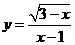 中,自变量
中,自变量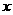 的取值范围是
.
的取值范围是
.
考点三 函数值的确定.
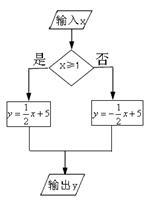
例题.(2008四川省南充)根据下面的运算程序,若输入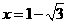 时,输出的结果y=
.
时,输出的结果y=
.

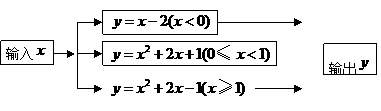





思路点拨:函数值是值在自变量取值范围内,与自变量相对应的函数的值,通常是将自变量的值代入函数解析式计算,就可以求出函数值.
解析:根据问题中所给程序,对于自变量取值范围不同,所对应的函数解析式就不一样
当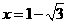 时
时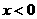 ,所对应的函数为
,所对应的函数为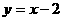 ,所以
,所以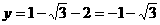
 规律总结:对于自变量不同对应函数解析式不同的函数,注意对应关系和自变量的范围.
规律总结:对于自变量不同对应函数解析式不同的函数,注意对应关系和自变量的范围.
[针对训练]
1(2008上海市)已知函数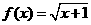 ,那么
,那么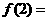 .
.
1.(2008成都市)在函数y=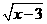 中,自变量x的取值范围是( ).
中,自变量x的取值范围是( ).
(A)x≥ - 3 (B)x≤ - 3 (C)x≥ 3 (D )x≤ 3
3.(2008年陕西省)生态公园计划在园内的坡地上造一片有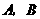 两种树的混合体,需要购买这两种树苗2000棵.种植
两种树的混合体,需要购买这两种树苗2000棵.种植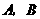 两种树苗的相关信息如下表:
两种树苗的相关信息如下表:
 |
单价(元/棵) |
成活率 |
劳务费(元/棵) |
|
A |
15 |
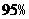 |
3 |
|
B |
20 |
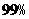 |
4 |
设购买 种树苗
种树苗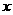 棵,造这片林的总费用为
棵,造这片林的总费用为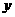 元.解答下列问题:
元.解答下列问题:
(1)写出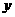 (元)与
(元)与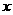 (棵)之间的函数关系式;
(棵)之间的函数关系式;
(2)假设这批树苗种植后成活1960棵,则造这片林的总费用需多少元?
考点二 函数自变量的取值范围的确定.
例题.(2008乐山市)函数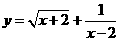 的自变量x的取值范围为( )
的自变量x的取值范围为( )
 A、x≥-2 B、x>-2且x≠2 C、x≥0且≠2 D、x≥-2且≠2
A、x≥-2 B、x>-2且x≠2 C、x≥0且≠2 D、x≥-2且≠2
思路点拨:求函数自变量的取值范围主要有:(1)分母不等于0;(2)算术平方
根的被开方数是非负数;(3)零指数和负指数幂的底数不能为0.利用这些限制条
件列不等式(组)就可以求出自变量的取值函数.
解析:由题知,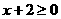 且
且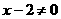 ,所以
,所以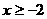 ,且
,且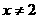 选 D .
选 D .
规律总结:注意函数由几部分组成时是求解集的公共部分.
[针对训练]
2.(2008 湖南 益阳)乘坐益阳市某种出租汽车.当行驶 路程小于2千米时,乘车费用都是4元(即起步价4元);当行驶路程大于或等于2千米时,超过2千米部分每千米收费1.5元.
(1)请你求出x≥2时乘车费用y(元)与行驶路程x(千米)之间的函数关系式;
(2)按常规,乘车付费时按计费器上显示的金额进行“四舍五入”后取整(如记费器上的数字显示范围大于或等于9.5而小于10.5时,应付车费10元),小红一次乘车后付了车费8元,请你确定小红这次乘车路程x的范围.
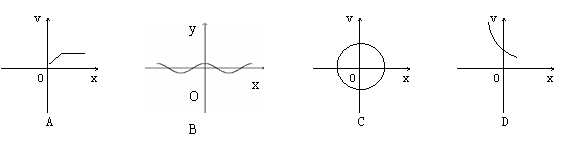
1.(2008广安市)下列图形中的曲线不表示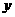 是
是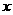 的函数的是(
)
的函数的是(
)
3.了解函数值的意义,能在具体函数中根据自变量的值求函数值.
2.了解函数自变量的意义,会求简单函数的自变量的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com