
题目列表(包括答案和解析)
2.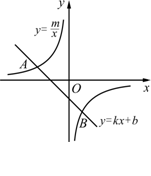 (2007四川资阳)如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数
(2007四川资阳)如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数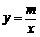 的图象的两个交点.
的图象的两个交点.
(1) 求此反比例函数和一次函数的解析式;
(2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
 3(2007四川成都)如图,一次函数
3(2007四川成都)如图,一次函数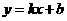 的图象与反比例函数
的图象与反比例函数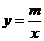 的图象交于
的图象交于 两点.
两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求 的面积.
的面积.
考点五 反比例函数的应用.
 例题. (2008四川巴中市)为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量
例题. (2008四川巴中市)为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量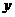 (mg)与燃烧时间
(mg)与燃烧时间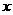 (分钟)成正比例;燃烧后,
(分钟)成正比例;燃烧后,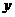 与
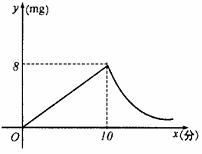
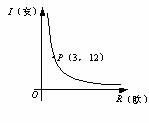
与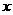 成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
(1)求药物燃烧时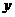 与
与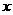 的函数关系式.
的函数关系式.
(2)求药物燃烧后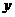 与
与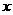 的函数关系式.
的函数关系式.
(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?
思路点拨:利用反比例函数解决实际问题,首先根据题目中所给条件
求出反比例函数的解析式,在利用反比例函数的性质解决相关问题.
 本题中含药量
本题中含药量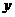 与燃烧时间
与燃烧时间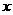 之间的关系是由两个部分组成,要分别求出,由特殊点(10,8)容易求出两个函数的解析式,再根据反比例函数的性质求出学生回教室的时间.
之间的关系是由两个部分组成,要分别求出,由特殊点(10,8)容易求出两个函数的解析式,再根据反比例函数的性质求出学生回教室的时间.
解析:(1)设药物燃烧阶段函数解析式为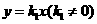 ,由题意点(10,8)在图象上,所以
,由题意点(10,8)在图象上,所以 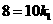
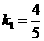 .
. 此阶段函数解析式为
此阶段函数解析式为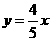
(2)设药物燃烧结束后的函数解析式为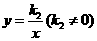 ,由题意 (10,8)在图象上所以
,由题意 (10,8)在图象上所以

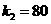 .
. 此阶段函数解析式为
此阶段函数解析式为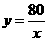
(3)当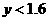 时,得
时,得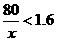
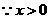
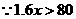
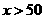
 从消毒开始经过50分钟后学生才可回教室.
从消毒开始经过50分钟后学生才可回教室.
规律总结:反比例函数的应用问题关键是先根据问题中的条件求出反比例函数的解析式,再用函数性质解决问题.待定系数法仍然是求函数解析的常用方法.
 [针对训练]
[针对训练]
1.(2008山东青岛)如果点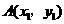 和点
和点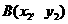 是直线
是直线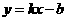 上的两点,且当
上的两点,且当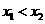 时,
时,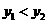 ,那么函数
,那么函数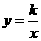 的图象大致是( )
的图象大致是( )
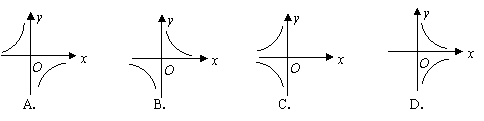

2.(2007四川绵阳)若A(a1,b1),B(a2,b2)是反比例函数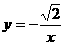 图象上的两个点,且a1<a2,则b1与b2的大小关系是( )
图象上的两个点,且a1<a2,则b1与b2的大小关系是( )
A.b1<b2? B.b1 = b2? C.b1>b2? D.大小不确定
考点四 反比例函数与一次函数的结合.
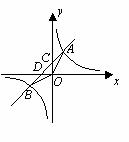
例题(2008四川内江)如图,一次函数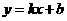 的图象经过第一、二、三象限,且与反比例函数图象相交于
的图象经过第一、二、三象限,且与反比例函数图象相交于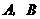 两点,与
两点,与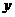 轴交于点
轴交于点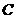 ,与
,与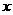 轴交于点
轴交于点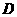 ,
,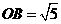 .且点
.且点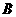 横坐标是点
横坐标是点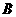 纵坐标的2倍.
纵坐标的2倍.
 (1)求反比例函数的解析式;
(1)求反比例函数的解析式;
(2)设点 横坐标为
横坐标为 ,
,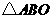 面积为
面积为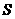 ,求
,求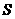 与
与 的函数关系式,并求出自变量的取值范围.
的函数关系式,并求出自变量的取值范围.
 思路点拨:反比例函数常与一次函数结合,利用一次函数求反比例函数,利用反比例函数性质求一次函数,或两者结合一起解决问题,本题利用B点的坐标的特征求出反比例函数,再根据反比例函数求一次函数解析式,进而求出
思路点拨:反比例函数常与一次函数结合,利用一次函数求反比例函数,利用反比例函数性质求一次函数,或两者结合一起解决问题,本题利用B点的坐标的特征求出反比例函数,再根据反比例函数求一次函数解析式,进而求出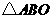 的面积与m的函数关系式.
的面积与m的函数关系式.
解析:(1)设点B坐标为(2t,t),由题意得
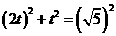 ,解得t =-1。
,解得t =-1。
故反比例函数的解析式是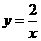 。
。
(2)由一次函数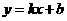 经过
经过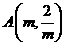 、
、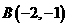 得
得
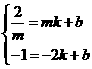 ,解得
,解得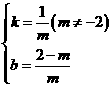 ,所以函数解析式为
,所以函数解析式为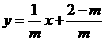
故点D坐标为(m-2,0),则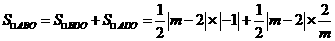
因为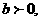 所以有
所以有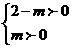 或
或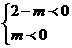 ,解得
,解得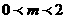 ,
,
故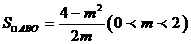 。
。
规律总结:一次函数与反比例函数的结合,常利用它们的交点坐标作为解决问题的突破口而使问题得到解决,同时把握两种函数的图象和性质是解决问题的关键.
[针对训练]
1.(2008资阳)若A(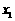 ,
,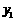 )、B(
)、B(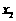 ,
,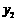 )在函数
)在函数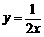 的图象上,则当
的图象上,则当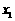 、
、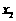 满足_______________时,
满足_______________时,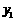 >
>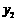 .
.
2.(2008广西南宁)如图是反比例函数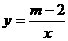 的图象,那么实数
的图象,那么实数 的取值范围是
的取值范围是
考点三 反比例函数的性质.
例题. (2008四川内江)若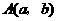 ,
,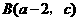 两点均在函数
两点均在函数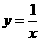 的图象上,且
的图象上,且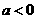 ,则
,则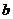 与
与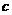 的大小关系为( )
的大小关系为( )
 A.
A.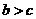 B.
B.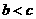 C.
C.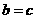 D.无法判断
D.无法判断
思路点拨:反比例函数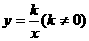 ,当
,当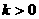 ,对于每一个分支,y随x的增大而减小;当
,对于每一个分支,y随x的增大而减小;当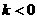 ,对于每一个分支,y随x的增大而增大.
,对于每一个分支,y随x的增大而增大.
解析:由题意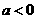 ,则A、B 两点在同一分支上,且
,则A、B 两点在同一分支上,且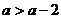 ,
,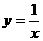 ,
,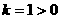 ,在每个分支上y随x的增大而减小,所以
,在每个分支上y随x的增大而减小,所以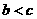 ,选 B .
,选 B .
规律总结:反比例函数y随x的变化情况必须分成两个分支,在整个定义范围内增减规律不成立,这也是常见错误.
[针对训练]
1.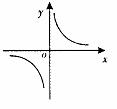 (2008甘肃兰州)若反比例函数
(2008甘肃兰州)若反比例函数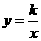 的图象经过点
的图象经过点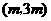 ,其中
,其中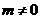 ,则此反比例函数的图象在( )
,则此反比例函数的图象在( )
A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象限
2.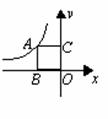 (2008浙江宁波)如图,正方形
(2008浙江宁波)如图,正方形 的边长为2,反比例函数
的边长为2,反比例函数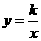 过点
过点 ,
,
则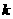 的值是( )
的值是( )
A.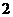 B.
B.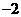 C.
C.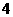 D.
D.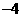
考点二 反比例函数的图象
例题.(2008四川泸州)对于反比例函数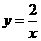 ,下列说法正确的是( )
,下列说法正确的是( )
A.点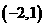 在它的图像上
B.它的图像经过原点
在它的图像上
B.它的图像经过原点
C.它的图像在第一、三象限 D.当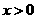 时,
时,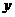 随
随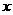 的增大而增大
的增大而增大
 思路点拨:反比例函数
思路点拨:反比例函数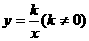 的图象是双曲线,当
的图象是双曲线,当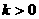 两个分支在第一 三象限;
两个分支在第一 三象限;
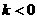 两个分支在二 四象限,判断点是否在图象上,将点的坐标代入解析式看是否成立.
两个分支在二 四象限,判断点是否在图象上,将点的坐标代入解析式看是否成立.
解析:显然点(-2,1)的坐标代入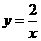 不能成立,二反比例函数中自变量的取值范围是
不能成立,二反比例函数中自变量的取值范围是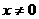 ;
;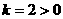 ,函数的两个分支在第一 三象限,所以答案C 是正确的;而
,函数的两个分支在第一 三象限,所以答案C 是正确的;而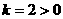 当
当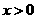 时,y随x的增大而减小.所以选 C .
时,y随x的增大而减小.所以选 C .
规律总结:反比例函数的图象是由系数k确定,而确定k的另一办法是根据图象上一个点的坐标,横纵坐标的乘积就是k的值.
[针对训练]
1、(2007浙江金华)下列函数中,图象经过点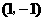 的反比例函数解析式是( )
的反比例函数解析式是( )
A.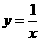 B.
B.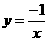 C.
C.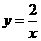 D.
D.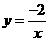
4.灵活应用反比例函数的图象和性质解决简单的实际问题,并会结合情景体会反比例函数的意义.
试题特点:反比例函数是初中函数的重要组成部分,是每套中考试卷必考内容,主要以考查反比例函数的定义、图象和性质,试题难度为低、中档为主,部分地区与二次函数结合作为压卷题,题量约占总题量的8%左右,各类题中都会出现
命题趋势:据近几年中考对反比例函数的考查可以看到:一是能否准确的把握反比例函数的概念及性质,能否根据解析式确定图象或根据图象确定解析式.二是能否与一次函数或二次函数结合解决相关问题,能否利用反比例函数的图象和性质解决生活中的实际问题.
复习建议:重在对概念和性质的把握,要充分利用函数图象,建立数形结合的思想和方法,注意与一次函数和二次函数的结合,且忌背性质,要在理解的基础上去认识和把握.
金题精析:
考点一:确定反比例函数的解析式..
 例题。(2007南充)已知反比例函数的图象经过点(3,2)和(m,-2),则m的值是__.
例题。(2007南充)已知反比例函数的图象经过点(3,2)和(m,-2),则m的值是__.
思路点拨:反比例函数的解析式为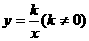 ,求反比例函数解析式就是确定k ,将反比例函数图象上一点的坐标代入就可以求出k的值.
,求反比例函数解析式就是确定k ,将反比例函数图象上一点的坐标代入就可以求出k的值.
解析:设反比例函数的解析式为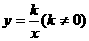 ,因为图象经过点(3,2),所以
,因为图象经过点(3,2),所以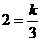 ,解得
,解得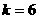 ,所以反比例函数的解析式为
,所以反比例函数的解析式为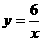 ,而点(m,-2)也在函数图象上,代入得,
,而点(m,-2)也在函数图象上,代入得,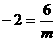 ,
,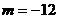
规律总结:确定反比例函数解析式常使用待定系数法,建立方程求解,一般是利用图象上点的坐标,有的问题情景中需要先求出函数图象上一个点的坐标或坐标的乘积,再确定解析式.
[针对训练]
3. 掌握反比例函数的性质,并能利用性质判断函数值的变换规律.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com