
题目列表(包括答案和解析)
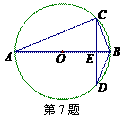
7.如图,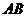 是
是 的直径,
的直径,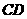 为弦,
为弦,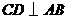 于
于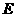 ,
,
则下列结论中不成立的是
A.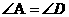 B.
B.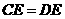
C.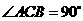 D.
D.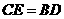
6.要判断小刚的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的
 A.方差 B.中位数
A.方差 B.中位数
C.平均数 D.众数
5.
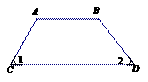
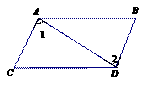
 下列图形中,由
下列图形中,由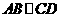 ,能得到
,能得到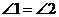 的是
的是
A B C D
数学试题第1页(共4页)中考资源网
4.下列运算,正确的是
A.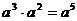 B.
B.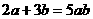 C.
C.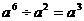 D.
D.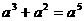
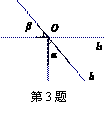
3. 如图,直线l1与l2相交于点O,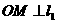 ,若
,若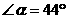 ,则
,则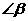 等于
等于
A.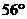 B.
B.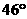
C.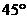 D.
D.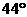
2.今年5月的某一天,参观上海世博会的人数达到450000,用科学记数法表示这个数为
 A.
A.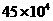 B.
B. 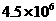 C.
C. 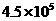 D.
D. 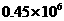
1. 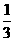 的相反数是
的相反数是
A.3 B.-3 C.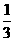 D.
D.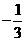
23.(本小题满分14分)如图9,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=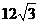 cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以
cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以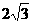 cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
(1)求∠OAB的度数.
(2)以OB为直径的⊙O‘与AB交于点M,当t为何值时,PM与⊙O‘相切?
(3)写出△PQR的面积S随动点移动时间t的函数关系式,并求s的最小值及相应的t值.
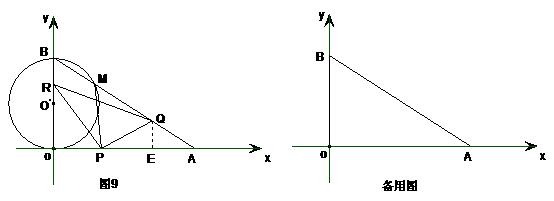 (4)是否存在△APQ为等腰三角形,若存在,求出相应的t值,若不存在请说明理由.
(4)是否存在△APQ为等腰三角形,若存在,求出相应的t值,若不存在请说明理由.
解:(1)在Rt△AOB中:
tan∠OAB=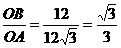
∴∠OAB=30°
(2)如图10,连接O‘P,O‘M. 当PM与⊙O‘相切时,有∠PM O‘=∠PO O‘=90°,
△PM O‘≌△PO O‘
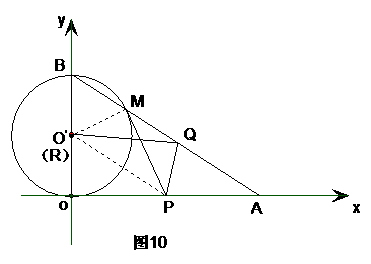 由(1)知∠OBA=60°
由(1)知∠OBA=60°
∵O‘M= O‘B
∴△O‘BM是等边三角形
∴∠B O‘M=60°
可得∠O O‘P=∠M O‘P=60°
∴OP= O O‘·tan∠O O‘P
=6×tan60°=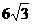
又∵OP=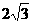 t
t
∴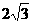 t=
t=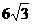 ,t=3
,t=3
即:t=3时,PM与⊙O‘相切.
(3)如图9,过点Q作QE⊥x于点E
∵∠BAO=30°,AQ=4t
∴QE=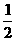 AQ=2t
AQ=2t
AE=AQ·cos∠OAB=4t×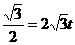
∴OE=OA-AE=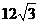 -
-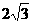 t
t
∴Q点的坐标为(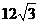 -
-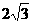 t,2t)
t,2t)
S△PQR= S△OAB -S△OPR -S△APQ -S△BRQ
=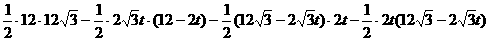
=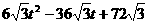
=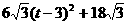 (
(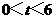 )
)
 当t=3时,S△PQR最小=
当t=3时,S△PQR最小=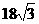
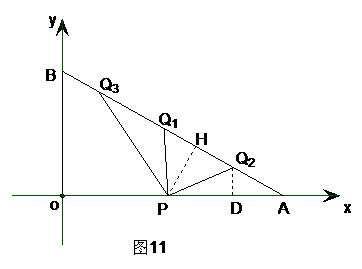
(4)分三种情况:如图11.
1当AP=AQ1=4t时,
∵OP+AP=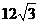
∴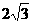 t+4t=
t+4t=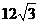
∴t=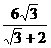
或化简为t=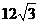 -18
-18
2当PQ2=AQ2=4t时
过Q2点作Q2D⊥x轴于点D,
∴PA=2AD=2A
Q2·cosA=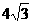 t
t
即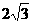 t+
t+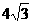 t =
t =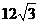
∴t=2
3当PA=PQ3时,过点P作PH⊥AB于点H
AH=PA·cos30°=(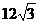 -
-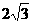 t)·
t)·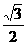 =18-3t
=18-3t
AQ3=2AH=36-6t
得36-6t=4t,
∴t=3.6
综上所述,当t=2,t=3.6,t=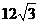 -18时,△APQ是等腰三角形.
-18时,△APQ是等腰三角形.
22.(本小题满分11分)二次函数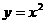 的图像如图8所示,请将此图像向右平移1个单位,再向下平移2个单位.
的图像如图8所示,请将此图像向右平移1个单位,再向下平移2个单位.
(1)画出经过两次平移后所得到的图像,并写出函数的解析式.
(2)求经过两次平移后的图像与x轴的交点坐标,指出当x满足什么条件时,函数值大于0?
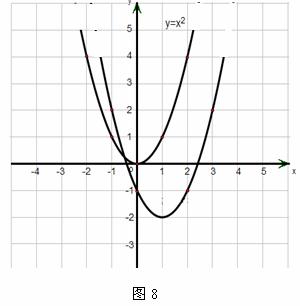 解:画图如图所示:
解:画图如图所示:
依题意得: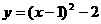
=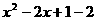
=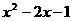
∴平移后图像的解析式为: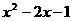
(2)当y=0时,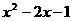 =0
=0
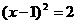
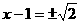
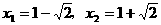
∴平移后的图像与x轴交与两点,坐标分别为(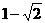 ,0)和(
,0)和(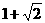 ,0)
,0)
由图可知,当x<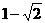 或x>
或x>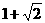 时,二次函数
时,二次函数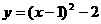 的函数值大于0.
的函数值大于0.
21.(本小题满分9分)师徒二人分别组装28辆摩托车,徒弟单独工作一周(7天)不能完成,而师傅单独工作不到一周就已完成,已知师傅平均每天比徒弟多组装2辆,求:
(1)徒弟平均每天组装多少辆摩托车(答案取整数)?
(2)若徒弟先工作2天,师傅才开始工作,师傅工作几天,师徒两人做组装的摩托车辆数相同?
解:(1)设徒弟每天组装x辆摩托车,则师傅每天组装(x+2)辆.依题意得:
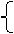 7x<28
7x<28
7(x+2)>28
解得2<x<4
∵x取正整数 ∴x=3
(2)设师傅工作m天,师徒两人所组装的摩托车辆数相同.
依题意得:3(m+2)=5m
解得:m=3
答:徒弟每天组装3辆摩托车;若徒弟先工作2天,师傅工作3天,师徒两人做组装的摩托车辆数相同.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com