8. 直角三角形的两边长分别为3和4，那么第3边的长为______________.

7.命题“一等腰三角形的底角相等”的逆命题是______________.

6．已知，如图，在⊿ABC中，AB=AC，点D在AC上，且BD=BC=AD，则∠A的度数为(　 )　

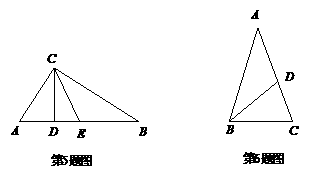(A)30°；　　

(B)45°；

　(C)36°；　　

(D)72°.

5．如图，在Rt△ABC中，CD 是斜边AB上的高，CE是斜边AB上的中线，那么下列结论中不正确的是(　　　 )

(A)∠ACD=∠B;　　　　　　　　　　 (B)∠ECB=∠DCE;　　

(C)∠ACD=∠ECB;　　　　　　　　　 (D)∠ECB=∠A-∠ECD.

4．若等腰三角形腰上的高等于腰长的一半，那么等腰三角形的顶角等于(　　 )度.

(A)60°或120°；(B)30°或150°；　　 (C)150°；　　　　　 (D) 30°.

3.直角三角形两条直角边长为3cm和4cm，斜边上的高为(　　　　 )

(A)3cm　　　　 (B)2cm　　　　　　 (C)2.4cm　　　　　 (D)3.6cm

2.三角形三边的垂直平分线的交点是三角形的　　　　　　　　　　　 (　　 )[来源:学。科。

(A)垂心；　　 (B)重心；　　　　 (C)内心；　　　　 (D)外心.

1.一个三角形的两边长分别是4，9，而第三边长为奇数，则第三边长是(　　 ).

(A)3或5或7；　 (B) 5或7或9；　 (C) 7或9或11；　 (D) 9或11或13.

　　　　　　　　　　　　　　　　　　　　 　图形与几何(3)

(三角形、等腰三角形、直角三角形)

8．掌握判定两个直角三角形全等的特殊方法；掌握直角三角形的有关性质和判定。在勾股定理及其逆定理的学习中，通过充分展开定理导出的过程和揭示它在度量几何中的作用，进一步理解形数之间的联系。会用等腰三角形的判定定理和性质定理证明简单的几何问题。