3．解分式方程、无理方程限于简单情形。知道用换元法解分式方程的条件，会用换元法或整体代换思想解分式方程；不要求用换元法解无理方程(在无理方程中含有未知数的根式不超过两个)

2．建立分式、根式与方程的联系，理解分式方程、无理方程的概念；领会把分式方程整式化、无理方程有理化的转化思想，掌握这两类方程的解法。

1．知道整式方程的概念；通过对含有一个字母系数、次数不超过二次的一元整式方程求解，体会分类讨论的思想方法，会解这类方程。

八年级第二学期第二十一章 代数方程(19课时)。

25．如图，有两个转盘，左边的转盘被平均分为4等分，右边的转盘被平均分为5等分，并分别涂上红蓝两种颜色.“配紫色游戏”的规则是：分别旋转两个转盘，若其中一个转盘转出红色，另一个转出蓝色，则可配成紫色，此时小刚得1分，否则小明得1分.

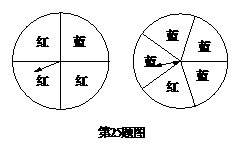这个游戏对双方公平吗？若认为公平，请说明理由；若你认为不公平，如何修改规则才能使游戏对双方公平？

24．某人有红、白、蓝三件衬衫，红、白、蓝三件长裤，该人任意拿一件衬衫和一条长裤，正好是一套白的概率为多少？

23．三张除字母外完全相同的纸牌，字母分别是K、K、Q，每次抽一张为一次实验，经过多次实验后结果汇总如下表：

实验总次数	10	20	50	100	200	300	400	500	1000	…
摸出K的频数	7	13	28		172	198	276		660	…
摸出k的频率				75%				62%		…

(1)将上述表格补充完整；

(2)观察表格，估计摸到K的概率约为多少？

(3)求摸到K的概率.

22．三张纸牌点数为1，2，3，将每张纸牌对折并裁开分成两个半张，共6个半张充分洗匀后，第一次抽出一个半张不放回，又抽出一个半张，问两次抽出的半张牌恰好还原成一张牌的概率是多少？

20．有10张卡片，每张卡片分别写有1，2，3，4，5，6，7，8，9，10．从中任意摸取一张卡片，问摸到2的倍数的卡片的概率是多少？3的倍数呢？5的倍数呢？

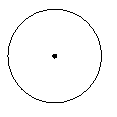　 　21.请在右图中设计一个转盘，使得自由转动这个转盘，指针停在白色和红色区域上的概率分别为.

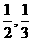19．请将下列事件发生的概率标在下图中.

(1)太阳4月20日从西边升起；

(2)在10瓶饮料中，有2瓶已过保质期，从中任取一瓶，恰好是已过保质期的饮料；

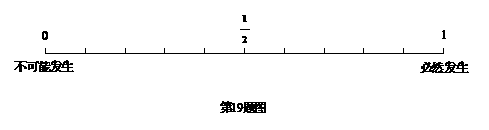(3)一个三角形的三条中线交于一点；

(4)在一个箱子中放有一个红球和两个黄球，随意拿出一个，拿出黄球的可能性.