
题目列表(包括答案和解析)
5.知道两条直线相交只有一个交点,它们所成的角(大小在0°到180°之内)有四个;理解对顶角和邻补角的概念,掌握对顶角的性质;会用交角的大小来描述两条相交直线的位置特征;知道垂线的概念和性质,会画已知直线的垂线,会用尺规作线段的垂直平分线。
4.理解余角和补 角的概念,会求已知角的余角和补角。
角的概念,会求已知角的余角和补角。
3.理解线段的中点、角的平分线的概念,掌握它们的画法;会用尺规作角的平分线。
1.理解两条线段相等、两个角相等的含义。
2 .会用直尺、圆规进行关于线段相等、角相等的作图(关于线段的和、差、倍与角的和、差、倍的作图问题,不限定为严格的尺规作图)。
.会用直尺、圆规进行关于线段相等、角相等的作图(关于线段的和、差、倍与角的和、差、倍的作图问题,不限定为严格的尺规作图)。
六年级第二学期:第七章 线段与角的画法 (9课时)
七年级第二学期:第十三章 相交线 平行线(13课时)
八年级第一学期:第十九章 几何证明19.4-19.6(5课时)
例1 如图2,已知在△ABC中,AD、CE为高,求证:△BDE∽△BAC.
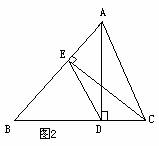 分析:首先凸显△BAD和△BCE,可证明相似,即可得到比例式
分析:首先凸显△BAD和△BCE,可证明相似,即可得到比例式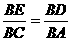 ,进而再凸显△BDE和△BAC,可根据两边对应成比例且夹角相等,两三角形相似.
,进而再凸显△BDE和△BAC,可根据两边对应成比例且夹角相等,两三角形相似.
证明:∵AD、CE为高,
∴∠ADB=∠BEC=900
在△BAD和△BCE中 ………(凸显思想的符号化表示)
∵∠ADB=∠BEC,∠B=∠B
∴△BAD∽△BCE
∴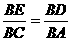
在△BDE和△BAC中 ……… (凸显思想的符号化表示)
∵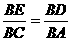 ,∠B=∠B
,∠B=∠B
∴△BDE∽△BAC
例2 如图3,平行四边形ABCD中,直线EF∥AB,在EF上任取两点E、F,连结AE、BF、DE、CF,分别交于G、H,连结GH.
求证:GH∥BC
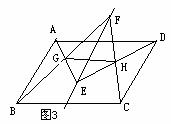 分析:本例如何探寻“中间比”来过渡“
分析:本例如何探寻“中间比”来过渡“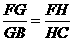 ”是证题的关键,可分别凸显△BAG和△FEG,△DCH和△EFH,即可得“中间比
”是证题的关键,可分别凸显△BAG和△FEG,△DCH和△EFH,即可得“中间比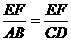 ”
”
证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD.
又∵EF∥AB,
∴AB∥EF∥CD.
∴△BAG∽△FEG,△DCH∽△EFH. …………(凸显思想的体现)
∴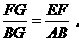
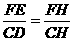 .
.
∴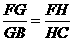
即GH∥BC
例3
如图,E、F为△ABC边AB、AC上两点,且AE=AF,连结EF并延长交BC的延长线于D点,求证: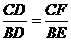 .
.
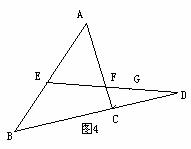
分析:对所证比例式分析后,容易想到从点C处引平行线,沟通已知条件和结论之间的联系.
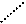
证明:过点C 作CG∥BA,交DE于G,
 ∴△BAG∽△FEG,△DCH∽△EFH……(凸显思想的体现)
∴△BAG∽△FEG,△DCH∽△EFH……(凸显思想的体现)
∴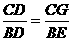 ,
,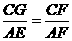
又∵AE=AF,
∴CF=CG
即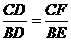 .
.
例4 如图5,路边有两根电线杆相距4米,分别在高为3米的A处和6米的C处用铁丝将两杆固定,求铁丝AD与铁丝将两杆固定,求铁丝AD与铁丝BC的交点M处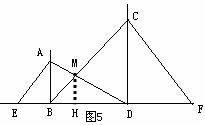 离地面的高MH.
离地面的高MH.
分析:要求MH的值,先行探究MH与AB、CD之间的关系,即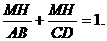
解:由题意,AB∥MH∥CD
∴△DMH∽△DAB,△BMH∽△BCD……(凸显思想的体现)
∴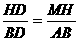 ①,
①,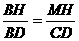 ②
②
①+②得: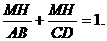
∴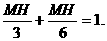
∴MH=2米.
即M离地面的高MH=2米.
凸显图形是一种思想,也是一种意识,要求同学们在今后的学习过程中能通过练习,多积累一些基本图形、常见图形及其性质,这样才能在解题中一路高歌、过关斩将.
其实初中几何中,最典型的凸显图形思想莫过于在全等三角形的学习,如图1:
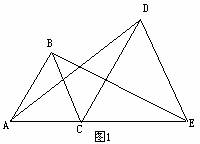 在△ACD和△BCE中
在△ACD和△BCE中
∵AC=BC,∠ACD=∠BCE,CD=CE
∴△ACD≌△BCE(SAS)
其中语句“在△ACD和△BCE中”即为凸显的最典型应用.
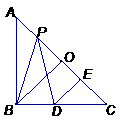
25.如图,在等腰直角三角形ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,DE⊥AC,垂足为点E . 求证:(1)PE=BO;(2)设AC=2,AP=x,四边形PBDE的面积为y,求y与x之间的函数关系式,并写出函数的定义域.
. 求证:(1)PE=BO;(2)设AC=2,AP=x,四边形PBDE的面积为y,求y与x之间的函数关系式,并写出函数的定义域.
24. (12分) 老师请同学们在一张长为17cm,宽为16cm的长方形纸板上,剪下一个腰长为10cm的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边上).请你帮同学们计算剪下的等腰三角形的面积.
23. (本题12分),△
(本题12分),△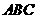 是等边三角形,点
是等边三角形,点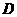 、
、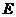 、
、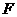 分别是线段
分别是线段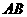 、
、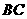 、
、 上的点.
上的点.
(1)若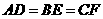 ,求证:△
,求证:△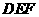 是等边三角形;
是等边三角形;
(2)若△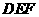 是等边三角形,求证:
是等边三角形,求证: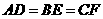 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com