
题目列表(包括答案和解析)
1.设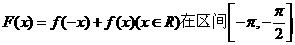 上是单调递减函数,将F(x)的图象按向量
上是单调递减函数,将F(x)的图象按向量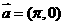 平移后得到函数G(x)的图象,则G(x)的一个单调递增区间是
平移后得到函数G(x)的图象,则G(x)的一个单调递增区间是
A.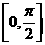 B.
B.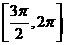 C.
C.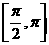 D.
D.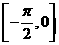
8.已知函数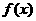 的定义域是
的定义域是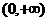 ,且满足
,且满足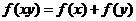 ,
,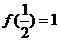 ,如果对于
,如果对于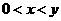 ,都有
,都有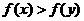 ,(1)求
,(1)求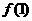 ;
;
(2)解不等式
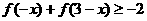 。
。
7.已知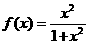 ,那么
,那么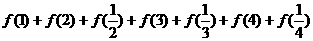 =_____。
=_____。
6.奇函数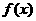 在区间
在区间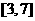 上是增函数,在区间
上是增函数,在区间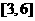 上的最大值为
上的最大值为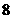 ,最小值为
,最小值为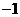 ,则
,则 __________。
__________。
5.已知定义在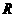 上的奇函数
上的奇函数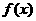 ,当
,当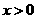 时,
时,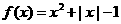 ,那么
,那么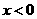 时,
时,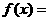 .
.
4.已知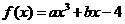 其中
其中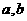 为常数,若
为常数,若 ,则
,则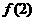 的值等于
的值等于
A.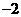 B.
B.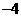 C.
C.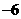 D.
D.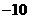
3.下列四个命题:(1)函数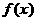 在
在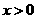 时是增函数,
时是增函数,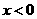 也是增函数,所以
也是增函数,所以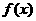 是增函数;(2)若函数
是增函数;(2)若函数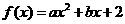 与
与 轴没有交点,则
轴没有交点,则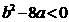 且
且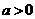 ;(3)
;(3) 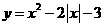 的递增区间为
的递增区间为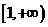 ;(4)
;(4) 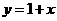 和
和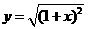 表示相等函数。
表示相等函数。
其中正确命题的个数是
A. B.
B.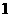 C.
C.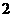 D.
D.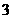
2.若函数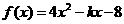 在
在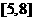 上是单调函数,则
上是单调函数,则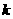 的取值范围是
的取值范围是
A.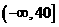 B.
B.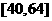
C.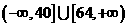 D.
D.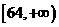
1.下列判断正确的是
A.函数 是奇函数
B.函数
是奇函数
B.函数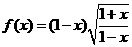 是偶函数
是偶函数
C.函数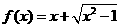 是非奇非偶函数 D.函数
是非奇非偶函数 D.函数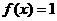 既是奇函数又是偶函数
既是奇函数又是偶函数
20. (本小题满分14分)已知函数f(x)=ax--2lnx,f(1)=0.
(1)若函数f(x)在其定义域内为单调函数,求a的取值范围;
(2)若函数f(x)的图象在x=1处的切线的斜率为0,且an+1=f′()-n2+1,已知a1=4,求证:an≥2n+2.
解:(1)因为f(1)=a-b=0,所以a=b,
所以f(x)=ax--2lnx,
所以f′(x)=a+-.
要使函数f(x)在定义域(0,+∞)内为单调函数,
则在(0,+∞)内f′(x)恒大于等于0或恒小于等于0.
当a=0时,则f′(x)=-<0在(0,+∞)内恒成立;适合题意.
当a>0时,要使f′(x)=a(-)2+a-≥0恒成立,则a-≥0,解得a≥1;
当a<0时,由f′(x)=a+-<0恒成立,适合题意.
所以a的取值范围为(-∞,0]∪[1,+∞).
(2)根据题意得:f′(1)=0,即a+a-2=0,得a=1,
所以f′(x)=(-1)2,
于是an+1=f′()-n2+1=(an-n)2-n2+1
=a-2nan+1.
用数学归纳法证明如下:
当n=1时,a1=4=2×1+2,
当n=2时,a2=9>2×2+2;
假设当n=k(k≥2且k∈N*)时,不等式ak>2k+2成立,即ak-2k>2成立,
则当n=k+1时,ak+1=ak(ak-2k)+1>(2k+2)×2+1=4k+5>2(k+1)+2,
所以当n=k+1,不等式也成立,
综上得对所有n∈N*时,都有an≥2n+2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com