5.(2009·辽宁高考)曲线y＝在点(1，－1)处的切线方程为　　　　　　　　　 (　)

A．y＝x－2 　　　　　　　　B．y＝－3x+2

C．y＝2x－3 　　　　　　　D．y＝－2x+1

解析：y′＝()′＝，∴k＝y′|_x＝1＝－2.

l：y+1＝－2(x－1)，即y＝－2x+1.

答案：D

4．设f(x)＝(ax+b)sinx+(cx+d)cosx，试确定常数a，b，c，d，使得f′(x)＝xcosx.

解：由已知f′(x)＝′

＝′+′

＝(ax+b)′sinx+(ax+b)(sinx)′+(cx+d)′cosx+(cx+d)·(cosx)′

＝asinx+(ax+b)cosx+ccosx－(cx+d)sinx

＝(a－cx－d)sinx+(ax+b+c)cosx.

又∵f′(x)＝xcosx，

∴必须有即

解得a＝d＝1，b＝c＝0.

3．(2009·安徽高考)设函数f(x)＝x³+x²+tanθ，其中θ∈，则导数f′(1)的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A． 　　　　B．[，]　　　 C．[，2] 　　　　D．[，2]

解析：∵f′(x)＝sinθ·x²+cosθ·x，

∴f′(1)＝sinθ+cosθ＝2sin(θ+)．

∵θ∈，∴θ+∈[，]．

∴sin(θ+)∈[，1]，∴f′(1)∈[，2]．

答案：D

2．设f₀(x)＝cosx，f₁(x)＝f₀′(x)，f₂(x)＝f₁′(x)，…，f_n+1(x)＝f_n′(x)，n∈N，则f₂₀₁₀(x)＝　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 (　)

A．sinx　 　　　B．－sinx　　　　 C．cosx 　　　　D．－cosx

解析：∵f₁(x)＝(cosx)′＝－sinx，f₂(x)＝(－sinx)′＝－cosx，f₃(x)＝(－cosx)′＝sinx，f₄(x)＝(sinx)′＝cosx，…，由此可知f_n(x)的值周期性重复出现，周期为4，

故f₂₀₁₀(x)＝f₂(x)＝－cosx.

答案：D

1.设f(x)＝xlnx，若f′(x₀)＝2，则x₀＝　　　　　　　　　　　　　　　　　 (　)

A．e²　 　　　　B．e　　　　 C.　 　　　　D．ln2

解析：f′(x)＝x×+1×lnx＝1+lnx，由1+lnx₀＝2，

知x₀＝e.

答案：B

8．已知回归方程＝4.4x+838.19，则可估计x与y的增长速度之比约为________．

解析：x与y的增长速度之比即为回归方程的斜率的倒数＝＝.

7.对有线性相关关系的两个变量建立的回归直线方程＝a+bx中，回归系数b　　 (　)

A．可以小于0　 　　　　B．大于0 　　　　　C．能等于0　 　　D．只能小于0

解析：因为b＝0时，r＝0，这时不具有线性相关关系，但b能大于0也能小于0.

答案：A

6．在一段时间内，某种商品价格x(万元)和需求量y(吨)之间的一组数据为：

(1)画出散点图；

(2)求出y对x的回归直线方程，并在(1)的散点图中画出它的图象；

(3)如果价格定为1.9万元，预测需求量大约是多少(精确到0.01吨)?

解：(1)散点图，如图．

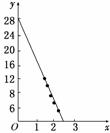
(2)采用列表的方法计算a与回归系数b.

＝×9＝1.8，＝×37＝7.4，

b＝＝－11.5，

a＝7.4+11.5×1.8＝28.1，

y对x的回归直线方程为

＝a+bx＝28.1－11.5x.

(3)当x＝1.9时，

y＝28.1－11.5×1.9＝6.25，

所以价格定为1.9万元时，需求量大约是6.25吨．

5．下表是某厂1-4月份用水量(单位：百吨)的一组数据，

由其散点图知，用水量y与月份x之间有较好的线性相关关系，其线性回归方程是＝－0.7x+a，则a＝________.

解析：＝2.5，＝3.5，

∴a＝－b＝3.5－(－0.7)×2.5＝5.25.

答案：5.25

4.以下是两个变量x和y的一组数据：

则这两个变量间的线性回归方程为　　　　　　　　　　　　　　　　　　　　　 　　　　　　　 (　)

A.＝x²　 　　　　　　B.＝　　　　　　 C.＝9x－15　 　　　　　D.＝15x－9

解析：根据数据可得＝4.5，＝25.5，

＝204，_iy_i＝1 296.

b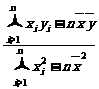＝＝＝9，

a＝－b＝25.5－9×4.5＝－15.

∴＝9x－15.

答案：C