
题目列表(包括答案和解析)
9.(2010湖北八校模拟,14)数列{an}中,Sn是前n项和,若a1=1,an+1=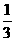 Sn(n≥1),则an=__________.
Sn(n≥1),则an=__________.
[答案]an=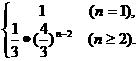
[解析]∵an+1=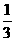 Sn,
①
Sn,
①
∴an=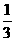 Sn-1.
②
Sn-1.
②
①-②得an+1-an=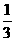 an,
an,
∴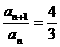 (n≥2).
(n≥2).
∵a2=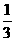 S1=
S1=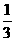 ×1=
×1=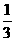 ,
,
∴当n≥2时,an=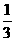 ×(
×(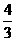 )n-2.
)n-2.
∴an=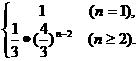
8.已知数列{an}的前n项和Sn=1-5+9-13+17-21+…+(-1)n-1(4n-3),那么S15+S22-S31的值为_________________.
[答案]-76
[解析]S15=1-5+9-13…+57=1+(9-5)+(17-13)+…+(57-53)=29,
同理可得:S22=-44,S31=61,
∴S15+S22-S31=-76.
7.(2010全国大联考,10)已知数列{an}满足an= 则{an}的前?2k-1项的和为( )
则{an}的前?2k-1项的和为( )
A.k2-k+1-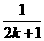 B.k2+k+1-
B.k2+k+1-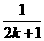
C.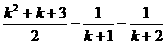 D.
D.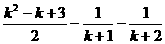
[答案]A
[解析]取k=1,S1=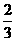 ,排除B、C;取k=2,S3=
,排除B、C;取k=2,S3=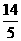 ,排除D。
,排除D。
6.Sn=1+ +…+
+…+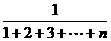 等于( )
等于( )
A.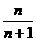 B.
B.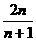 C.
C.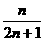 D.
D.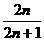
[答案]B
[解析]an=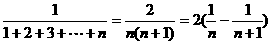 ,
,
∴Sn=2[(1-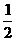 )+(
)+(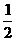 -
-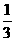 )+…+(
)+…+(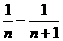 )]
)]
=2(1-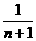 )
)
=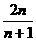 .
.
5.数列1,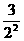 ,
,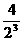 ,
,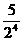 ,…,
,…,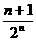 的前n项和等于( )
的前n项和等于( )
A.Sn=3-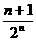 -
-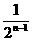 B.Sn=3-
B.Sn=3-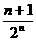 -1-
-1-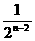
C.Sn=3-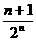 -
-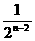 D.Sn=3-n2n-
D.Sn=3-n2n-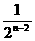
[答案]A
[解析]令Sn=1+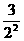 +
+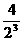 +…+
+…+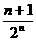 ,
①
,
①
则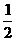 Sn=
Sn=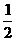 +
+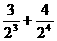 +…+
+…+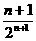 .
②
.
②
①-②得
∴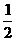 Sn=1+
Sn=1+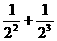 +…+
+…+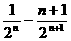
=1+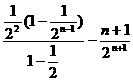
=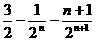 .
.
∴Sn=3-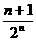 -
-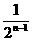 ,故选A.
,故选A.
或者用特殊法.
4.数列1,(1+2),(1+2+22),…,(1+2+22+…+2n-1),…的前n项和等于( )
A.2n B.2n-n C.2n+1-n-2 D.n·2n
[答案]C
[解析]令n=1,排除A、D,又令n=2,排除B.选C.
3.数列{an}的通项公式为an=4n-1,令bn=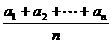 ,则数列{bn}的前n项和为( )
,则数列{bn}的前n项和为( )
A.n2 B.n(n+2) C.n(n+1) D.n(2n+1)
[答案]B
[解析]∵an=4n-1,∴数列{an}是等差数列,且a1=4-1=3,
∴bn=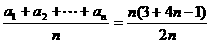 =2n+1.
=2n+1.
显然数列{bn}是等差数列,且b1=2+1=3,
它的前n项和Sn=b1+b2+…+bn=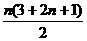 =n(n+2).
=n(n+2).
2.数列{an}的通项公式是an=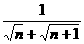 ,若前n项和为10,则项数n为( )
,若前n项和为10,则项数n为( )
A.11 B.99 C.120 D.121
[答案]C
[解析]因an=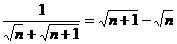 ,
,
故Sn=(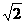 -1)+(
-1)+(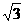 -
-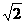 )+…+(
)+…+(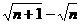 )=
)=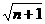 -1,
-1,
由Sn=10,故n=120.
1.数列{an}的前n项和Sn=2n2-3n+1,则a4+a5+a6+…+a10等于( )
A.171 B.21 C.10 D.161
[答案]D
[解析]原式=S10-S3=2×102-3×10-(2×32-3×3)=161.
14.已知a>1,设P:a(x-2)+1>0,Q:(x-1)2>a(x-2)+1,试寻求使得P、Q都成立的x集合.
解析:由题意得:
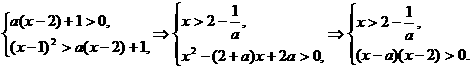
若1<a<2,则有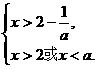
而a-(2-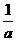 )=a+
)=a+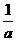 -2>0,所以a>2-
-2>0,所以a>2-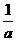 ,
,
故x∈{x|x>2或2-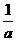 <x<a};
<x<a};
若a=2,则有x∈{x|x>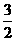 ,且x≠2};
,且x≠2};
若a>2,则有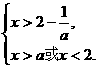
若x∈{x|x>a或2-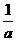 <x<2}.
<x<2}.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com