
题目列表(包括答案和解析)
1.填空题
(1)已知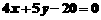 ,用含x的代数式表示y,得______________________.
,用含x的代数式表示y,得______________________.
当
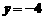 时,x=_____________________________.
时,x=_____________________________.
(2)已知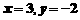 是关于x、y的方程
是关于x、y的方程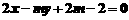 的解,则:m=__________.
的解,则:m=__________.
(3)已知
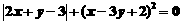 ,则
,则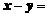 _________.
_________.
(4)已知关于x、y的方程组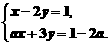 的解x与y相等,则
的解x与y相等,则 .
.
4.能应用二元一次方程组解决简单的实际问题.
中招考点
二元一次方程概念及解法,代入法和加减法解方程组,用含一个未知数的代数式表示另一个未知数,会检验未知数的一组对应值是否为二元一次方程的解,能应用二元一次方程组解决简单的实际问题.
典型例题
例1 解下列方程组:
(1)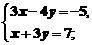
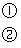 (2)
(2)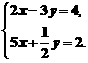
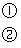
分析:要结合方程组中方程的系数特征,合理选择消元的方法.通常方程中系数比较简单,尤其当一个未知数系数的绝对值是1时,可选用代入消元法,一般常采用加减消元法.
解:(1)由②得
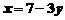 .
.
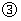
代入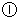 ,得
,得
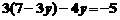 .
.
解得
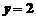 .
.
代入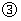 ,得
,得
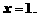
所以方程组的解是
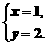

(2)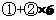 ,得
,得
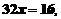
即
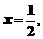
代入 ,得
,得
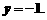
所以方程组的解是
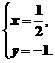
例2 已知关于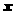 、
、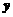 的方程组
的方程组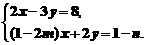 与
与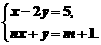 有相同的解,求m、n值.
有相同的解,求m、n值.
分析:这里两个方程组中都有待定系数,但并未知道具体的解,不能应用方程解的定义,代入后转化为关于m、n的方程来解.注意到两个方程组中都有一个方程的系数是已知的.且根据方程组的解的定义,本题“相同的解”也就是方程组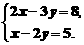 的解,因此,这个解可以先予求出:
的解,因此,这个解可以先予求出: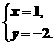 这时再将它代入另两个方程组,得
这时再将它代入另两个方程组,得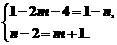
解这个方程组,得 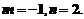
例3 某公园的学生门票价格如下:
|
购 票 人 数 |
1~50 |
51~100 |
100以上 |
|
每
人 票
价(元) |
13 |
11 |
9 |
(1)初一甲、乙两个班共104人,若分别购票,需1240元.两个班合起来购票,能否节约一些?或已知甲班人数稍多一些,请求出两班各有多少人?
(2)若不知道两班学生总数及各班人数的多少,你能求出各班人数吗?
分析 本题具有较大的开放性.在第(1)个问题中,首先应根据题意,判断各班人数的大致范围:两班共104人,则至少有一个班级人数50,但总票价1240元不是11的倍数,说明另一个班级人数不超过50.根据这些信息,可以着手应用列方程组求解.
在第二个问题中,减弱了条件,两班学生的总数也是未知数.比较上述分析,共同之处是两班人数不可能是同一范围内的数(因为1240不是13、11、9的倍数),不同之处是少了一个方程.则应该用到求二元一次方程的整数解的知识,同时还应根据实际情况,选取合适的解.
解(1)设初一甲班学生x人,初一 乙班学生y人,根据题意,两班票价总数1240不是13或11的倍数,所以甲班人数大于50,乙班人数小于50.可得方程组
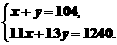
解这个方程组,得 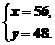 经检验,符合题意.
经检验,符合题意.
答:初一甲班学生56人,初一乙班学生48人.
(2)设两个班级人数分别为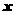 人和y人,根据实际情况,其中x、y的值是不超过100的正整数,且
人和y人,根据实际情况,其中x、y的值是不超过100的正整数,且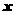 <y.根据题意,得方程
<y.根据题意,得方程
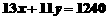 .
.
将方程变形为含x的代数式表示y,得
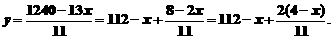
所以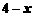 是11的倍数,依次取
是11的倍数,依次取
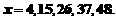
求出对应的
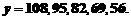
根据实际情况,我们选取甲、乙两班人数分别为37人、69人、69人、37人、48人、56人或56人、48人四种比较合理的解答.
强化训练
3.会灵活应用代入消元法和加减消元法解二元一次方程组.
2.了解二元一次方程组、方程组的解、解方程组等基本概念,掌握用消元法解方程组的基本思想;通过“消元”,转化为一元一次方程.
1.了解二元一次方程组及其解的概念,会将二元一次方程化为用含一个未知数的代数式表示另一个未知数的形式,会检验未知数的一组对应值是否为二元一次方程的解.
8.应用方程解下列问题:
(1)某车间原计划每周装配36台机床,预计若干周完成任务,在装配了三分之一后,改进操作技术,功效提高了一倍,结果提前一周半完成任务.求这次任务需装配的机床总台数.
(2)某人有急事,预定搭乘一辆小货车从A地赶住B地,实际上他乘小货车行了三分之一路后改乘出租车,车速提高了一倍,结果提前一个半小时到达.已知小货车的车速是36千米/小时,求两地间的路程.
第6部分 二元一次方程组
课标要求
7.已知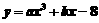 ,当
,当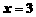 时,
时,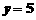 .求当
.求当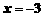 时,
时,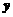 的值.
的值.
6.请你编制一道关于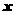 的方程,形如
的方程,形如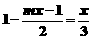 ,使它的解在1到2之间.
,使它的解在1到2之间.
5.初一(4)班课外乒乓球组买了两副乒乓球板,若每人付9元,则多了5元,后来组长收了每人8元,自己多付了2元,问两副乒乓球板价值多少?
4.当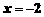 时,代数式
时,代数式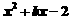 的值是12,求当
的值是12,求当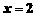 时,这个代数式的值.
时,这个代数式的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com