6.如图5-3-9,已知AB∥CD,求∠ABE+∠BED+∠EDC的度数.

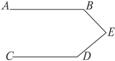
图5-3-9

解:∠ABE+∠BED+∠EDC=360°.

理由:过点E作FE∥AB,如图.

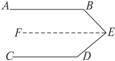
∵AB∥CD(已知),

∴CD∥EF(两条直线都和第三条直线平行,则两直线互相平行).∴∠B+∠BEF=180°,∠FED+∠D=180°.

∴∠ABE+∠BED+∠EDC=∠B+∠BEF+∠FED+∠D=360°.

5.如图5-3-8,已知BE∥DF,∠B=∠D,试说明:AD∥BC.

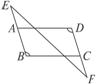
图5-3-8

证明:因为BE∥DF(已知),

所以∠D=∠EAD(两条直线平行,内错角相等).

因为∠B=∠D(已知),

所以∠B=∠EAD.

所以AD∥BC(同位角相等,两直线平行).

4.如图5-3-7所示,已知AB∥CD,EF分别交AB、CD于E、F,EG平分∠AEF,FH平分∠EFD,求证:EG∥FH.

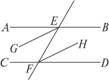
图5-3-7

证明:∵AB∥CD(已知),∴∠AEF=∠EFD(____________).

∵EG平分∠AEF,FH平分∠EFD(____________),

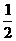∴∠____________=∠AEF,∠____________=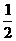∠EFD(角平分线定义).

∴∠____________=∠____________.

∴EG∥FH(____________).

解析:根据已知条件和图形,熟练证明步骤.

答案:两直线平行,内错角相等　 已知　 GEF

EFH　 GEF　 EFH　 内错角相等,两直线平行

3.如图5-3-6，AB∥DE，BC∥EF，∠2-∠1=90°，则∠1与∠2的度数分别为(　　 )

A.20°,110°　　　　　　　　　　　　　　　　 B.45°,135°

C.60°,120°　　　　　　　　　　　　　　　 　　D.30°,150°

解析:∵AB∥DE，∴∠1=∠DGC.∵∠2+∠DGC=180°，∴∠1+∠2=180°.又∵∠2-∠1=90°，∴∠1=45°，∠2=135°.

答案:B

2.如图5-3-5所示,已知∠1=100°,∠2=80°,∠3=50°,∠4=130°,则直线a与c的关系是(　　 )

A.相交　　　　　　　　 B.平行　　　　　　　 C.垂直　 　　　　　　D.异面

解析:因为∠1=100°,∠2=80°,

所以∠1+2=180°(已知).

所以a∥b(同旁内角互补,两直线平行).

同理c∥b.所以a∥c(平行于同一条直线的两条直线平行).

答案:B

1.如图5-3-4,如果AD∥BC,则有①∠A+∠B=180°;②∠B+∠C=180°;③∠C+∠D=180°.

上述结论中正确的是(　　 )

A.只有①　　　　　　　 B.只有②　　　　　　 C.只有③　　　　　　 D.只有①和③

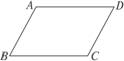
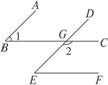
图5-3-4　　　　　　　 图5-3-5　　　　　　　 图5-3-6

解析:注意分清所得的“三线八角”,①由∠A+∠B=180°,得AD∥BC;②由∠B+∠C=180°,得AB∥CD;③由∠C+∠D=180°,得AD∥BC.故选D.

答案:D

5.如图5-3-3，DE∥BC，那么(　　 )

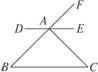
图5-3-3

A.∠EAC=∠B　　　　　　　　　　　　　　 B.∠FAE=∠C

C.∠DAC+∠C=180°　　　　　　　　　　　 D.∠DAB=∠EAC

解析:首先搞清各选项中两个角的位置关系，再根据平行线的性质作出判断.选项A、B、D中的两个角不是同位角,不是内错角,也不是同旁内角，∴它们不一定成立；选项C中两角是同旁内角，根据“两直线平行，同旁内角互补”得选项C成立.

答案:C

10分钟训练(强化类训练，可用于课中)

4.在①同位角,②内错角,③同旁内角;三类角中的角的平分线互相平行的是(　　 )

A.①③　　　　　　　　 B.①②　　　　　　 C.②③　　　　　　　 D.①②③

解析:如图所示，同位角、内错角的角平分线互相平行；同旁内角的角的平分线互相垂直.

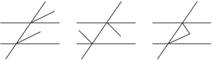
答案:B

3.如图5-3-2,已知AB∥CD，直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=40°,则∠EGF的度数是(　　 )

A.60°　　　　　　　　 B.70°　　　　　　 C.80°　　　　　　　 D.90°

解析:已知AB∥CD,所以∠EFG+∠BEF=180°.又因为∠EFG=40°,EG平分∠BEF,所以∠BEG=70°.又因为AB∥CD,∠EGF=∠BEG=70°,故选B.

答案:B

2.如图5-3-1,AC∥BD,∠A=70°,∠C=50°,则∠1=_________,∠2=_________,∠3=_________.

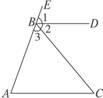
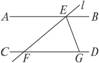
图5-3-1　　　　　 　　　图5-3-2

解析:因为AC∥BD,所以∠1=∠A=70°(两直线平行,同位角相等).

所以∠2=∠C=50°(两直线平行,内错角相等).

所以∠3=180°-∠1-∠2=180-70°-50°=60°.

答案:70°　 50°　 60°