
题目列表(包括答案和解析)
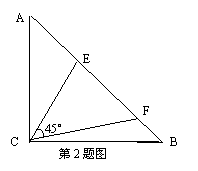
2、如图,已知△ABC中,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.(1)求证:△ACF∽BEC;(2)设△ABC的面积为S,求证:AF·BE=2S.
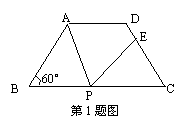
1、如图,在等腰梯形ABCD中,AD∥BC,AD=3㎝,BC=7㎝,∠B=60°,P为下底BC上一点(不与B、C重合),连结AP,过P点作PE交DC于E,使得∠APE=∠B.(1)求证:△ABP∽△PCE;(2)求等腰梯形的腰AB的长;(3)在底边BC上是否存在一点P,使得DE∶EC=5∶3?如果存在,求出BP的长,如果不存在,请说明理由.
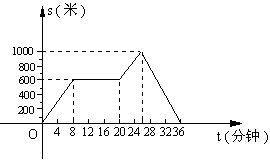
28、如下图,表示距离与时间之间的函数关系,请你根据这个图象,讲一个故事。
要求:有时间、地点、人物,要反映事件的全过程。(6分)
 ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
27、1998年湖北抗洪抢险中,某部队奉命派甲连跑步前住离驻地90千米的公安县抢险,1小时45分钟后,因险情加重,又增派乙连乘车前往支援。下图中,l1、l2分别表示两支部队前进路程S(千米)与时间t(时)之间的关系。(8分)
请根据图象回答下列问题:
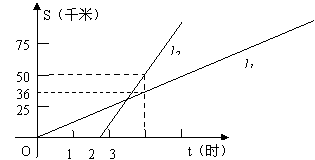 (3)l1、l2分别表示哪支部队行进的路程与时间之间的关系?
(3)l1、l2分别表示哪支部队行进的路程与时间之间的关系?
(4)分别计算两去部队到达目的地所需的时间。
(5)半小时内乙连能否赶上甲连?
(6)求乙连追上甲连的时间,并确定其位置。
26、下面的图象记录了某地一月份某天的温度随时间变化的情况,请你仔细观察图象回答下面的问题:(6分)
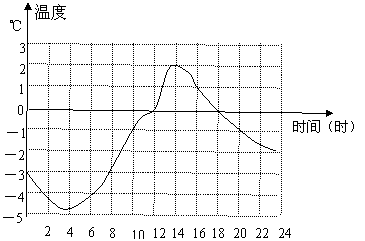
(1)20时的温度是_______℃,温度是0℃的时刻是_________时,最暖和的时刻是________时,温度在-3℃以下的持续时间为______小时.
(2)你从图象中还能获取哪些信息(至少写出2条)?
25.求下列各函数的自变量的取值范围(12分)
(7) y = (8) y =
(9) y = - (10)y=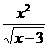
24、写出使下列二次根式有意义的条件(6分)
(5)
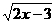 (6)
(6) 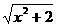
23、计算(16分)
(1)
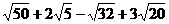 (2)
(2) 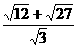
(3)
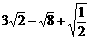 (4) 化简
(4) 化简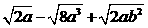 (b<0)
(b<0)
22、在平面直角坐标系中,若点(m,2)与(3,n)关于原点对称,则m+n的值是_______.
21、点M(-2,1)到x轴的距离为______。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com