
题目列表(包括答案和解析)
5. 在式子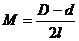 中
中
(1)已知M、l、d,求D; (2)已知 M、l、D,求d.
C组
4. 求出式子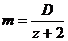 中的D
中的D
3. 求出式子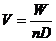 中的W
中的W
2. 解下列方程(y为未知数)
(1)3x+4y=5
(2)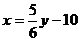
(3)ax+by=c(b≠0)
1.解下列方程(x为未知数)
(1)3a+4x=7x-5b (2)ax-by=0(a≠0)
(3)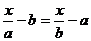 (a≠0) (4)
(a≠0) (4)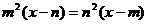 (m2≠n2)
(m2≠n2)
4.
当x________,分式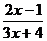 没有意义 5. 当x________,分式
没有意义 5. 当x________,分式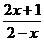 没有意义。
没有意义。
l 分式方程
分母里含有未知数的方程叫做分式方程。
例1 解方程 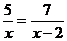
(分析:解分式方程的关键在于去分母,化分式方程为整式方程。由于要保证分式有意义,因此解出分式方程后,要检验方程的解)
解: 方程两边都乘______________,约去分母,得:
解这个整式方程
检验:
例2 解方程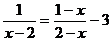
解:方程两边都乘__________,约去分母,得
解这个整式方程,得
检验:
练习:
A组
解下列分式方程
(1)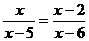 (2)
(2)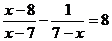
解: 解:
方程的两边都乘_________,约去分母,得 方程的两边都乘__________,约去分母,得
检验: 检验:
(3)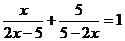 (4)
(4)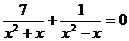
B组
解下列分式方程
(1)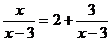 (2)
(2)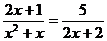
(3)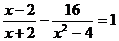 (4)
(4)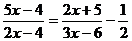
C组
解关于x的方程(即x为未知数,其它字母为已知数)
(1)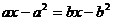 (2)
(2)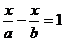
含有字母系数的方程(一)
l 定义:方程ax=b中,x是未知数,a和b是用字母表示的已知数,其中字母a是未知数x的系数,这样的方程叫做含字母系数的方程。
例1 解方程 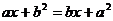 (a≠b)
(a≠b)
解:
例2解方程 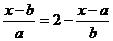 (a+b≠0)
(a+b≠0)
解:
练习:
3.
当x________,分式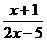 有意义; 当x_________这个分式没有意义。
有意义; 当x_________这个分式没有意义。
1.
当x________,分式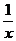 有意义。
2. 当x________,分式
有意义。
2. 当x________,分式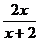 有意义。
有意义。
1.只言片语话三角形;
2.勾股定理知多少;
3.谈谈生活中的对称美;
4.感悟函数学习;
5.函数·方程·不等式;
6.一则数学日记;
7.“忽如一夜春风来,千树万树梨花开”,2001年9月,新课程在全国38个国家级实验区进行实验开始,新课程走进校园,走进了师生的生活,莘莘学子们切身感受到新课程带来的理念、目标、学法等各方面的变化,试结合“学用杯”数学知识应用竞赛,自拟题目,谈谈你的感受.
接着,他让大家交流讨论任意四边形全等的条件:
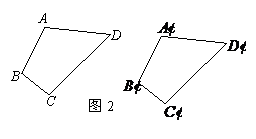 如图2,两个任意四边形
如图2,两个任意四边形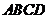 和
和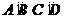 .
.
问:当满足什么条件时,就能保证它们全等?
小明:“我认为只要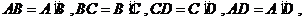 且
且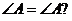 就能保证它们全等.”
就能保证它们全等.”
小强:“我认为只要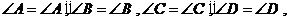 且
且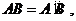 就能保证它们全等.”
就能保证它们全等.”
假设你作为第三人加入他们两人的讨论,你是如何看待他们的观点的?你还有其他判定两个任意四边形全等的方法吗?请自拟题目,写一篇200~400字的数学作文,阐述你的观点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com