
题目列表(包括答案和解析)
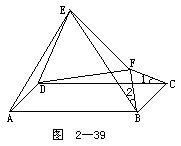
2.如图2-39所示.在平行四边形ABCD中,△ABE和△BCF都是等边三角形.求证:△DEF是等边三角形.
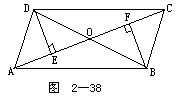
1.如图2-38所示.DE⊥AC,BF⊥AC,DE=BF,∠ADB=∠DBC.求证:四边形ABCD是平行四边形.
4.如果△ABC的周长为40米(m),以A,B,C三点为圆心,作三个半径为1米的圆轮,带动圆轮转动的皮带长为l,试求l的长度.
3.在题1中,如果考虑直线l和平行四边形更一般的关系(如平行四边形变成圆,或某一中心对称图形,垂线AA',BB',CC',DD'只保持平行等),那么又有什么结论,试作出你的猜想和证明.
2.在上题中,如果移动直线l,使它与四边形ABCD的位置关系相对变动得更特殊一些(如l过A,或l交AB,BC等),那么,相应地结论会有什么变化?试作出你的猜想和证明.
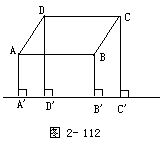
1.如图2-112.已知由平行四边形ABCD各顶点向形外一条直线l作垂线,设垂足分别为A',B',C',D'.求证:
'A+B'B=C'C+D'D.
2.特殊化、一般化在解题中的应用
例1 设x,y,z,w为四个互不相等的实数,并且
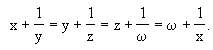
求证:x2y2z2w2=1
分析与解 我们先考虑一个特例,只取两个不同实数,简化原来命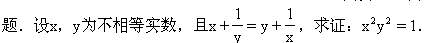
(1)求证这个特殊化的辅助问题就容易多了.事实上,因为
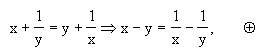
又因为
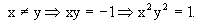
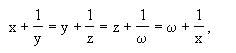
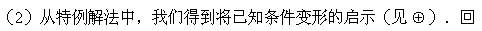 到原命题,由
到原命题,由
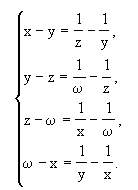
容易想到变形
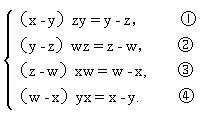
去分母变形为
①×②×③×④,并约去(x-y)(y-z)(z-w)(w-x)(利用x,y,z,w互不相等)就得到
x2y2z2w2=1.
例2 设凸四边形O1O2O3O4的周长为l,以顶点O1,O2,O3,O4为圆心作四个半径为R的圆轮.如果带动四个圆轮转动的皮带长为s,求s的长度(图2-110).
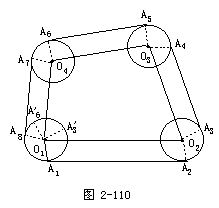
解(1)先解一个特例(图2-111).设只有两个圆轮⊙O1,⊙O2,2│O1O2│=l'.显然,带动两轮转动的皮带长度为
s=l'+2πR.
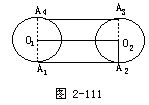
(2)再回到原题,我们猜想:
s=l+2πR.
以下证实这个猜想是正确的.
为此,设皮带s与各圆轮接触的四个弧为
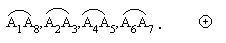
由于它们是等圆上的弧,因此,只要证出这四条弧恰好组成一个圆即可.
事实上,引O1A'3∥O2A3,由于O1A1∥O2A2,所以∠A1O1A' 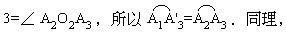
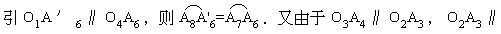
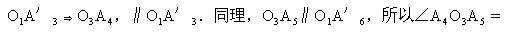
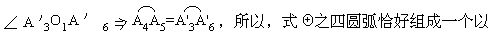 O1为圆心,以R为半径的圆.因此,四圆弧之长为2πR.又因为O1O2=A1A2,O2O3=A3A4,O3O4=A5A6,O1O4=A7A8,所以
O1为圆心,以R为半径的圆.因此,四圆弧之长为2πR.又因为O1O2=A1A2,O2O3=A3A4,O3O4=A5A6,O1O4=A7A8,所以
l=A1A2+A3A4+A5A6+A7A8.
所以,所求皮带长为
s=l+2πR.
例3 设a1,a2,…,an都是正数.试证:
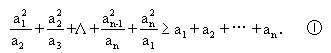
证 欲证①成立,先考虑最简单的情形,设n=3,即证
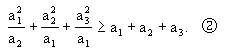
把②变形为
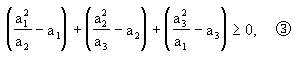
即证
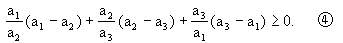
由于④中左边有(a1-a2),(a2-a3),(a3-a1),其和为零,因此,我们猜想:若④式左边相加,其和不小于(a1-a2),(a2-a3),(a3-a1)之和即可.为此,我们证更简单的事实.
设a,b是任意正整数,则有
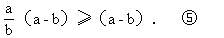
事实上,由(a-b)2≥0有
a2-ab≥ab-b2,
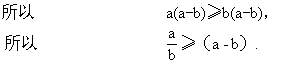
根据⑤,④显然成立,因为
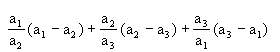
≥(a1-a2)+(a2-a3)+(a3-a1)≥0,
从而③式成立,②式成立.
剩下来的工作是把②式推到一般情形①,这是很容易的.因为根据⑤,①式必然成立,因为
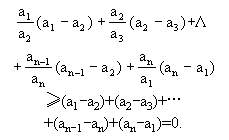
练习十九
1.特殊化、一般化和类比推广
命题1 在△ABC中,∠C=90°,CD是斜边上的高(图2-102),则有CD2=AD·BD.
这是大家所熟知的直角三角形射影定理.
类比命题1,如果CD是斜边上的中线,将怎样?由此得到命题2.
命题2 在△ABC中,∠C=90°, CD是斜边上的中线(图2-103),则有CD=AD=BD.
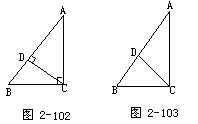
这便是大家已经学过的直角三角形中的斜边中点定理(在此定理中仍保持CD2=AD·BD).
再类比,如果CD是∠C的平分线,将怎样?于是得到命题3.
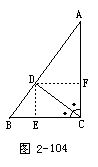
命题3 在△ABC中,∠C=90°,CD是∠C的平分线(图2-104),则有
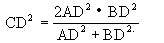
这是一个新命题,证明如下.
引DE⊥BC于E,DF⊥AC于F.
因为
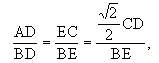
所以
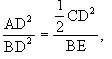
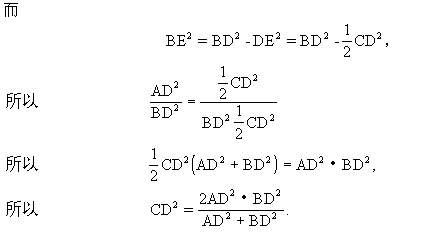
我们把命题1、命题2、命题3一般化,考虑D点是AB上任一点,便产生了以下两个命题.
命题4 在△ABC中,∠C=90°,D是斜边AB上的任一内分点(图2-105),则有
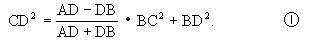
证 引DF⊥AC于F,DE⊥BC于E.因为
CD2-BD2=CE2-BE2=(CE-BE)BC,
而
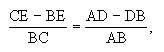
所以
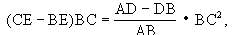
所以
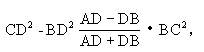
即
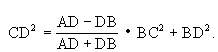
命题5 在△ABC中,∠C=90°,D是斜边AB上的任一外分点(图2-106),则有
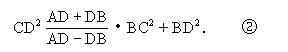
证 只要令命题4之结论中AD为-AD,则有
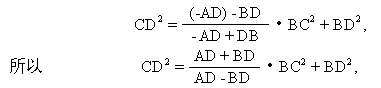
我们再把命题4和命题5特殊化,令D点与A点重合(即│AD│=0),那么无论是①式或②式都有
AB2=BC2+AC2.
这就是我们熟知的勾股定理.
命题4或命题5与通常形式下的广勾股定理是等效的,因此,它们也可称作广勾股定理.下面用命题4或命题5来证明以下定理.
定理 在△ABC中,AB=c,BC=a,AC=b,a在c上的射影为n,
时,取“-”号,∠B为钝角时,取“+”号).
证 我们仅利用命题4证图2-107中的情况(∠B<90°).
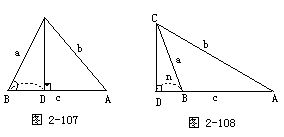
为此,我们作图2-109,其中∠DBA=90°,CD=x,CE⊥DB于E,并设CE=n.由命题4,立得
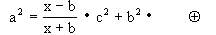
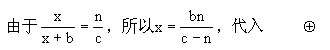
得
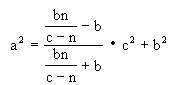
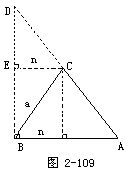
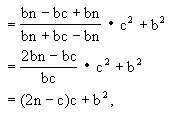
所以
b2=a2+c2-2cn.
同理可证图2-108(∠B>90°)的相应结论.
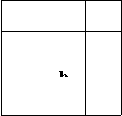
2.按如图所示的两种方式分割正方形,你能分别得到什么结论?
|
|
|
|
|
|||||
 |
 |
||||
(1) (2)
1. 利用因式分解计算: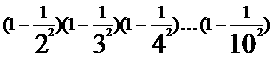
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com