1、骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化，在这一问题中，因变量是(　　　 )

A、沙漠　　　　　 B、体温　　　　　 C、时间　　　　　 D、骆驼

8．某水果批发市场香蕉的价格如下表：

若小强购买香蕉x千克(x大于40千克)付了y元，则y关于x的函数关系式为 　　　　。

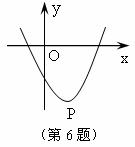
7．如图，某函数图象上的最低点P的坐标是(1，－3)，

则当x＞1，y随x的增大而　　　　　 　(填增大或减少)

6．已知函数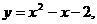当x=2时，函数值为　　　　 。

5．用描点法画函数图象的一般步骤是　　　　　　　　　　　　　　　　 。

4．若点A(m，2)在函数y=2x－6的图象上，则m的值为　　　　　　 。

3．表示函数常用的方法有　　　　　　 　　　　　　　　。

2．函数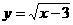的自变量x的取值范围是　　　　　　　　 。

1．直角三角形两锐角的度数分别为x、y，其关系式为y=90－x，其中变量为　　　　　 ，常量为　　　　 。

29、(8分)沙漠探险队的A组由驻地出发，以12公里/是垢速成度向东南方向搜索前进，同时，B组也由驻地出发，以9公里/时的速度向东北方向搜索前进。求2个小时后，A，B两组之间的距离。

※30、(8分)某单位为响应政府发出的全民健身的号召，打算在长和宽分别为20米和11米的矩形大厅内修建一个60平方米的矩形健身房ABCD。该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图)，已知装修旧墙壁的费用为20元/平方米，新建(含装修)墙壁的费用为80元/平方米. 设健身房的高为3米，一面旧墙壁AB的长为x米，修建健身房的总投入为y元。

(1)求y与x的函数关系式；

(2)为了合理利用大厅，要求自变量x必须满足8≤x≤12。当投入资金为4800元时，问利用旧墙壁的总长度为多少米？

※31、(10分)已知：□ABCD中，AB=6，对角线AC交BD于点O，△AOB的周长为15，求对角线AC、BD的和。

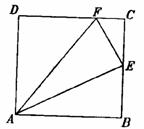※32、(10分)如图，在正方形ABCD中，E是BC的中点，F为CD上一点，且CF=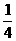CD。

求证：△AEF是直角三角形。