
题目列表(包括答案和解析)
5.下面这几个车标中,是中心对称图形而不是轴对称图形的共有 ( )
A.1 B.2 C.3 D.4

4.一个容量为80的样本最大值是141,最小值是50,取组距为10,则可以分成( )
A.10组 B.9组 C.8组 D.7组
3.用配方法解一元二次方程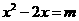 ,配方后的方程为( )
,配方后的方程为( )
A.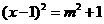 B.
B.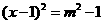
C.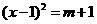 D.
D.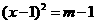
2.下列命题中,属于真命题的是( )
A.一个角的补角大于这个角 B.若a∥b,b∥c,则a∥c
C.若a⊥c,b⊥c,则a∥b D.互补的两角必有一条公共边
1.下列各式不成立的是( )
A.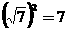 B.
B.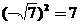 C.
C.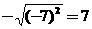 D.
D.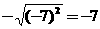
25、某地区一厂工业废气排放量为450万立方米,为改善该地区的大气环境质量,决定分二期投入治理,使废气的年排放量减少到288万立方米。如果每期治理中废气减少的百分率相同。(1)求每期减少的百分率是多少?(2)预计第一期治理中每减少1万立方米需投入3万元,第二期治理中每减少1万立方米废气需投入4.5万元。问两期治理完成后共需投入多少万元?
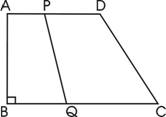 26、如图,梯形ABCD中,AD∥BC,∠B=Rt∠,AD=21cm,BC=24cm,动点P从点A出发沿AD边向D以1cm/s的速度运动,另一动点Q同时从点C出发沿CB边向点B以2cm/s的速度运动(运动到点B时,P、Q同时停止运动)。设点P运动时间为t.
26、如图,梯形ABCD中,AD∥BC,∠B=Rt∠,AD=21cm,BC=24cm,动点P从点A出发沿AD边向D以1cm/s的速度运动,另一动点Q同时从点C出发沿CB边向点B以2cm/s的速度运动(运动到点B时,P、Q同时停止运动)。设点P运动时间为t.
(1)t为何值时,四边形PQCD为平行四边形?
(2)t为何值时,四边形PQCD为等腰梯形?
24、如图,矩形ABCD中,AB=8,BC=6,画出面积不相等的三个菱形,使菱形的顶点都在矩形的边上,并分别求出所画菱形的面积。(下列图形供画图用)

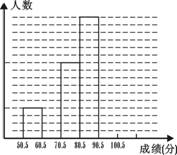
23、为了让学生了解环保知识,增强环保意思,某中学举行了一次“环保知识竞赛”,共有850名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计。请你根据尚未完成并有局部污染的频率分布表和频率分布直方图,解答下列问题:
|
分 组 |
频数 |
 频率 频率 |
|
50.5-60.5 |
4 |
0.08 |
|
60.5-70.5 |
|
0.16 |
|
70.5-80.5 |
10 |
|
|
80.5-90.5 |
16 |
0.32 |
|
90.5-100.5 |
|
|
|
合 计 |
50 |
1.00 |
(1)填充频率分布表的空格;
(2)补全频数直方图,并在此图上直接绘制频数分布折线图;
(3)在该问题中,总体、个体、样本和样本容量各是什么?
(4)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
22、解方程:
(1)X2=X (2)用配方法解方程:2X2-4X+1=0
21、计算:(1)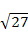 -3
-3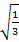 (2)已知a=3+2
(2)已知a=3+2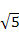 b=3-2
b=3-2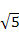
求a2b-ab2的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com