7.[05包头]若一次函数y=ax+1―a中，y随x的增大而增大，且它的图像与y轴交于正半轴，则|a―1|+=　　　　　　 　。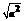

15、当k<0，b<0时，一次函数y=kx+b的图像不经过(　　 )象限。

A.四　　 B.三　　 C.二　　　 D.一

7、直线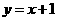不经过的象限是……………………………………………………(　)

A、第一象限　　　 B、第二象限　　　　　　 C、第三象限　　　　　　 D、第四象限

17、点A(a，2)、B(2b，3)都在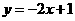上，则a与b的大小关系是(　　 )

(A)a＞b　　　　 (B) a ＜b　　　　 (C) a = b 　　　　 (D) 不能确定

系数对图象的影响

2、课前热身

7、链接生活：某服装厂现有甲种布料42米，乙种布料30米，计划用这两种布料生产M，L两种型号的校服共40件．已知做一件M型号的服装需要甲种布料0.8米，乙种布料1.1米，可获利45元；做一件L型号的服装需要甲种布料1.2米，乙种布料0.5米，可获利30元．设生产M型号服装x件，用这批布料生产两种型号的服装所获的利润为Y元，

　(1)写出y(元)与x(件)之间的函数关系式，并求出自变量的取值范围；

　(2)该厂生产这批校服时，当M型号校服为多少件时，能使该厂所获的利润最大？最大利润是多少？

(4)汽车由天津驶往相距120千米的北京，它的平均速度是30千米/时，则汽车距北京的路程s(千米)与行驶的时间t(小时)的函数关系用图象应为下图中的(　 )

(多媒体演示幻灯片)

某学校需要刻录一批电脑光盘，若电脑公司刻录，每张需要8元(含空白光盘费)；若学校自刻，除租用刻录机需120元外，每张还需成本费4元(含空白光盘费)．问刻录这批

电脑光盘，到电脑公司刻录费用少，还是自刻费用少？你能帮助设计出一种使刻录费用最少的刻录方案吗？

8、 已知两条直线y1＝2x-3和y2＝5-x．

(1)在同一坐标系内作出它们的图象；

(2)求出它们的交点A坐标；

(3)求出这两条直线与x轴围成的三角形ABC的面积；

(4)k为何值时，直线2k+1＝5x+4y与k＝2x+3y的交点在每四象限．

分析 (1)这两个都是一次函数，所以它们的图象是直线，通过列表，取两点，即可画出这两条直线．

(2)两条直线的交点坐标是两个解析式组成的方程组的解．

(3)求出这两条直线与x轴的交点坐标B、C，结合图形易求出三角形ABC的面积．

(4)先求出交点坐标，根据第四象限内的点的横坐标为正，纵坐标为负，可求出k的取值范围．

解 (1)

(2)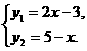　 解得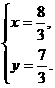

所以两条直线的交点坐标A为．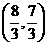

(3)当y1＝0时，x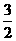＝所以直线y1＝2x-3与x轴的交点坐标为B(，0)，当y2＝0时，x＝5，所以直线y2＝5-x与x轴的交点坐标为C(5,0)．过点A作AE⊥x轴于点E，则．

(4)两个解析式组成的方程组为

解这个关于x、y的方程组，得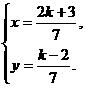

由于交点在第四象限，所以x＞0,y＜0．

即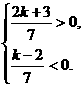　 解得．

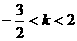例4 旅客乘车按规定可以免费携带一定重量的行李．如果所带行李超过了规定的重量，就要按超重的千克收取超重行李费．已知旅客所付行李费y(元)可以看成他们携带的行李质量x(千克)的一次函数为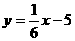．画出这个函数的图象，并求旅客最多可以免费携带多少千克的行李？

分析 求旅客最多可以免费携带多少千克的行李数，即行李费为0元时的行李数．为此只需求一次函数与x轴的交点横坐标的值．即当y＝0时，x＝30．由此可知这个函数的自变量的取值范围是x≥30．

解 函数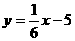(x≥30)图象为：

当y＝0时，x＝30.

所以旅客最多可以免费携带30千克的行李.

例5 今年入夏以来，全国大部分地区发生严重干旱．某市自来水公司为了鼓励市民节约用水，采取分段收费标准，若某户居民每月应交水费y(元)是用水量x(吨)的函数，当0≤x≤5时，y＝0.72x,当x＞5时，y＝0.9x-0.9．

(1)画出函数的图象；

(2)观察图象，利用函数解析式，回答自来水公司采取的收费标准.

分析 画函数图象时，应就自变量0≤x≤5和x＞5分别画出图象，当0≤x≤5时，是正比例函数，当x＞5是一次函数，所以这个函数的图象是一条折线.

解 (1)函数的图象是：

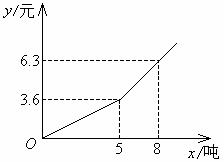
(2)自来水公司的收费标准是：当用水量在5吨以内时，每吨0.72元；当用水量在5吨以上时，每吨0.90元.

7、按照我国税法规定：个人月收入不超过800元，免交个人所得税．超过800元不超过1300元部分需缴纳5%的个人所得税．试写出月收入在800元到1300元之间的人应缴纳的税金y(元)和月收入x(元)之间的函数关系式．

．．

(应用)(可下一次用)

6、 已知A、B两地相距30千米，B、C两地相距48千米．某人骑自行车以每小时12千米的速度从A地出发，经过B地到达C地．设此人骑行时间为x(时)，离B地距离为y(千米)．

(1)当此人在A、B两地之间时，求y与x的函数关系及自变量x取值范围．

(2)当此人在B、C两地之间时，求y与x的函数关系及自变量x的取值范围．

分析 (1)当此人在A、B两地之间时，离B地距离y为A、B两地的距离与某人所走的路程的差．

(2)当此人在B、C两地之间时，离B地距离y为某人所走的路程与A、B两地的距离的差．

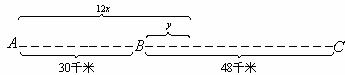
解 (1) y＝30－12x．(0≤x≤2.5)

(2) y＝12x－30．(2.5≤x≤6.5)

5、点(1，1)、(2，0)、(3，－1)是否在同一条直线上？