
题目列表(包括答案和解析)
4.已知,如图6-78,AB∥CD,BC∥DE,那么∠B+∠D=__________.
3.在△ABC中,∠C=2(∠A+∠B),则∠C=________.
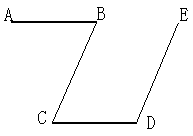
图6-78
2.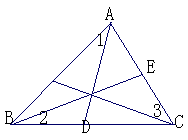 如图6-77,AD、BE、CF为△ABC的三条角平分线,则:∠1+∠2+∠3=________.
如图6-77,AD、BE、CF为△ABC的三条角平分线,则:∠1+∠2+∠3=________.
图6-77
1.命题“任意两个直角都相等”的条件是________,结论是___________,它是________(真或假)命题.
3.1旋转(1)
第1题.
 如图所示的图案,它可以看成是什么“基本图案”通过怎样的放置而得到到的?
如图所示的图案,它可以看成是什么“基本图案”通过怎样的放置而得到到的?
答案:解:图案是以一个叶片和柄为“基本图案”,通过连续四次旋转而形成,
旋转解度分别等于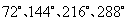 .
.
第2题. 如图可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
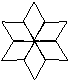
答案:解:一个菱形旋转5次得到的,旋转的角度分别为: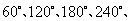
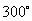 .
.
第3题. 如图,你能分析出图中的旋转现象吗?

答案:解:整个图形可以看做是图形的六分之一绕中心位置,按同一方向连续旋转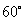
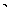
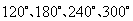 前后的图形共同组成的;
前后的图形共同组成的;
也可以看做是图形的三分之一绕中心位置,按同一方向旋转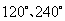 前后的图形共同组成的;
前后的图形共同组成的;
也可以看做是图形的二分之一绕中心位置旋转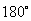 前后的图形共同组成的;
前后的图形共同组成的;
还可以看做是矩形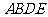 绕中心位置分别旋转
绕中心位置分别旋转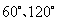 前后的图形共同组成的.
前后的图形共同组成的.
 第4题. 如图,可以看做是由一个三角形旋转而成的,它一共旋转 次,分别旋转 度而形成的.
第4题. 如图,可以看做是由一个三角形旋转而成的,它一共旋转 次,分别旋转 度而形成的.
答案:8 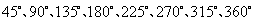
第5题. 如图,整个圆形可以看做是图形的 绕中心位置,按照同一方向连续旋转 前后的图形共同组成的,也可以看做是图形的 绕中心位置连续旋转 前后的图形共同组成的.还可以看做图形的 绕中心旋转 前后的图形共同组成的.

答案:八分之一 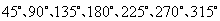 四分之一
四分之一 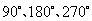
二分之一 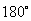
第6题. 如图,在正方形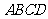 中,
中,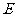 是
是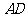 的中点,
的中点,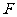 是
是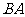 延长线上一点,
延长线上一点,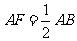 .问:(1)可以通过平移、翻折、旋转中的哪种方法,使
.问:(1)可以通过平移、翻折、旋转中的哪种方法,使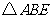 变到
变到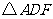 的位置?(2)指出图中线段
的位置?(2)指出图中线段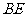 与
与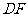 之间的关系.
之间的关系.

答案:(1)绕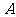 点逆时针旋转
点逆时针旋转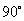 ;(2)相等.
;(2)相等.
第7题. 如图,下列四个图形都可以分别看做由一个“基本图案”经过旋转所形成,则它们中旋转角相同的图形为( )
A.(a)(b) B.(a)(d) C.(b)(c) D.(c)(d)
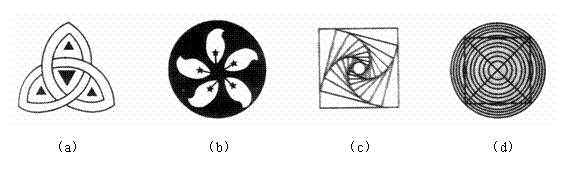
答案:D
第8题. 如图,矩形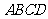 的边长
的边长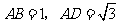 ,若矩形
,若矩形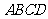 以
以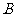 为中心,按顺时针方向旋转到
为中心,按顺时针方向旋转到 的位置(点
的位置(点 落在对角线
落在对角线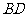 上),则
上),则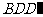 的形状为( )
的形状为( )
A.等腰三角形 B.等边三角形
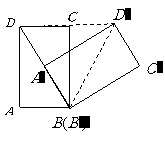 C.等腰直角三角形 D.无法确定
C.等腰直角三角形 D.无法确定
答案:B
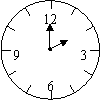
第9题. 如图所示,钟表的分针匀速旋转一周需要60分,在这个问题中,
(1)旋转中心是 .
(2)现在钟面上是2点,如果过10min,那么分针旋转了 度,时针旋转了
度.
(3)如果再经过15min,那么分针共旋转了 度,时针共旋转了 度.
 答案:(1)中心轴 (2)60 5 (3)
答案:(1)中心轴 (2)60 5 (3)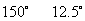
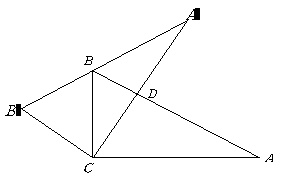
第10题. 如图,在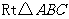 中,
中,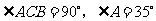 ,以直角顶点
,以直角顶点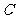 为旋转中心,将
为旋转中心,将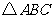 旋转到
旋转到 的位置,其中
的位置,其中 分别是
分别是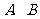 的对应点,且点
的对应点,且点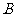 在斜边
在斜边 上,
上,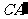 交
交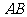 于
于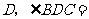 .
.
答案: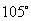
第11题. 钟表的分针旋转一周需要60分钟,时针旋转一周需要12小时,秒针旋转一周需要60秒则1小时时针旋转 度,分针旋转 度,秒针旋转 度,经过900秒,时针旋转 度,分针旋转 度,钞针旋转 度.
答案: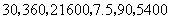
第12题. 记得雪花的样子吗?它可以看作是由什么“基本图案”通过怎样的变化得到的?
答案:略
第13题. 九点20分时,时针和分针的夹角是多少度?
答案: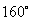
第14题. 如图,是否存在这样的两个三角形,其中一个是另一个通过旋转得到的?旋转多大角度?并进一步分析此图案的构成?
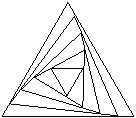
答案:存在 旋转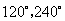
第15题. 请分析下图中的旋转现象.

答案:可以看成由图形的六分之一绕中心位置按同一方向连续旋转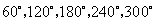 ,前后的图形共同组成.
,前后的图形共同组成.
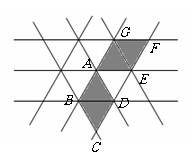
第16题. 如图,图中所有的小三角形均是全等的等边三角形,其中的菱形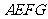 可以看成是把菱形
可以看成是把菱形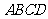 以
以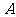 为中心( )
为中心( )
A.顺时针旋转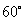 得到 B.顺时针旋转
得到 B.顺时针旋转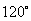 得到
得到
 C.逆时针旋转
C.逆时针旋转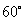 得到 D.逆时针旋转
得到 D.逆时针旋转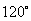 得到
得到
答案:D
第17题. 在图形旋转中,下列说法中错误的是( )
A.图形上的每一点到旋转中心的距离相等
B.图形上的每一点转动的角度相同
C.图形上可能存在不动点
D.图形上任意两点的连线与其对应两点的连线相等
答案:A
第18题. 在平面内,将一个图形沿 ,移动 ,这种图形运动叫平移.在平面内,将一个图形绕 ,沿 转动 ,这种图形运动叫旋转.平移、旋转只改变图形 ,不改变图形的 和 .
答案:一定的方向,一定的距离,某一个定点,一定的方向,一个角度,位置,大小,形状
第19题. 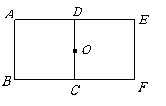 如图所示,如果四边形
如图所示,如果四边形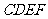 旋转后能与正方形
旋转后能与正方形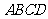 重合,则图形所在的平面上可以作为旋转中心的点有多少个?
重合,则图形所在的平面上可以作为旋转中心的点有多少个?
答案:解:观察图形,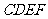 绕点
绕点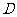 顺时针旋转
顺时针旋转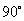 或绕点
或绕点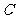 逆时针旋转
逆时针旋转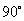 都可以与正方形
都可以与正方形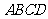 重合;且
重合;且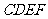 绕
绕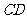 的中点
的中点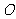 旋转
旋转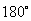 也可以与正方形
也可以与正方形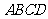 重合.因此可作为旋转中心的点有3个,分别是点
重合.因此可作为旋转中心的点有3个,分别是点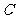 、点
、点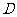 和点
和点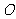 .
.
第20题. 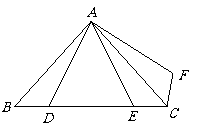 如图,
如图,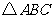 为等腰直角三角形,而
为等腰直角三角形,而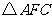 是由
是由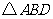 按顺时针方向旋转而来的,如果
按顺时针方向旋转而来的,如果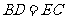 ,试问:(1)
,试问:(1)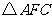 是由
是由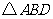 旋转多少度得到的?旋转中心在哪里?(2)
旋转多少度得到的?旋转中心在哪里?(2)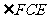 为多少度?(3)图中有哪几个全等三角形?
为多少度?(3)图中有哪几个全等三角形?
答案:解:(1)易知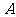 为旋转中心,由于
为旋转中心,由于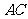 是
是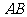 的旋转而得,
的旋转而得,
故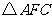 是由
是由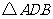 按顺时针旋转
按顺时针旋转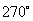 得到的.
得到的.
(2)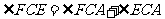
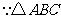 为等腰直角三角形形.
为等腰直角三角形形.
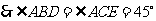 .
.
又 旋转不改变图形形状和大小.
旋转不改变图形形状和大小.
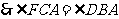 从而
从而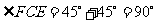 .
.
(3)在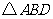 和
和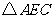 中,
中,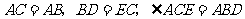
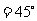 .
.
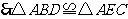 .
.
又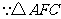 由
由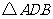 旋转而来.
旋转而来.
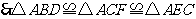 .
.
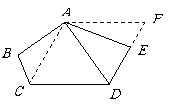
第21题. 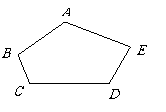 如图,在五边形
如图,在五边形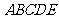 中,
中,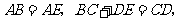
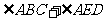
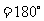 .试说明
.试说明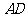 平分
平分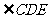 的理由.
的理由.
答案:解:如图,连结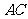 ,将
,将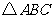 绕点
绕点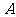 旋转
旋转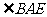 的度数到
的度数到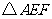 的位置,
的位置,
因为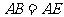 ,所以
,所以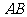 与
与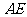 重合.
重合.
因为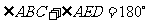 ,且
,且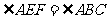 ,
,
所以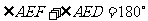 ,
,
所以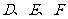 三点在一条直线上,
三点在一条直线上,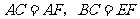 .
.
在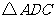 与
与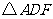 中,
中,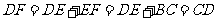 .
.
又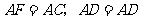 ,所以
,所以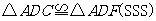 .
.
因此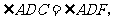 即
即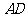 平分
平分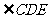 .
.
第22题. 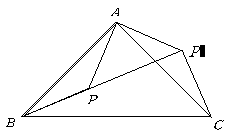 如图,
如图,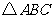 是直角三角形,
是直角三角形,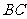 是斜边,将
是斜边,将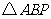 绕点
绕点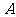 逆时针旋转后,能与
逆时针旋转后,能与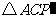 重合.如果
重合.如果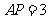 ,求
,求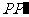 的长.
的长.
答案:解: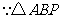 绕点
绕点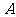 逆时针旋转后,能与
逆时针旋转后,能与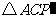 重合,
重合,

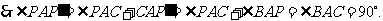
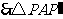 为等腰直角三角形,
为等腰直角三角形,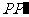 为斜边.
为斜边.
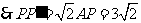 .
.
第23题. 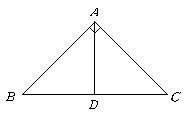 如图,
如图, 为等腰直角三角形,其中
为等腰直角三角形,其中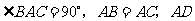 为高;以
为高;以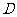 为旋转中心将
为旋转中心将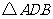 逆时针旋转
逆时针旋转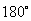 后构成新图形,试问此图形是什么?
后构成新图形,试问此图形是什么?
答案:解:如图,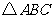 为等腰三角形,
为等腰三角形,
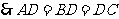 ,旋转后
,旋转后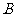 点与
点与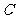 点重合.
点重合.
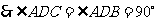 ,
,
 .
.
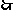 点
点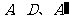 在一条直线上.
在一条直线上.
又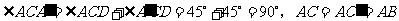 ,
,

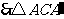 为等腰直角三角形.
为等腰直角三角形.
第24题. 如图,把直角三角形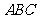 的斜边
的斜边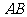 放在定直线
放在定直线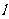 上,按顺时针方向在
上,按顺时针方向在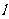 上转动两次,使它转到
上转动两次,使它转到 的位置.设
的位置.设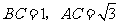 ,则顶点
,则顶点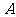 运动到点
运动到点 的位置时,点
的位置时,点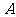 经过的路线与直线
经过的路线与直线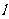 所围成的面积是多少?(计算结果不取近似值)
所围成的面积是多少?(计算结果不取近似值)
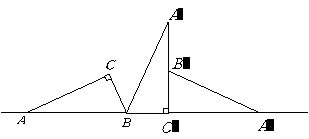
答案:解:由条件易知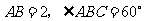 .
.
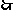 第一次以
第一次以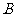 为旋转中心点
为旋转中心点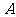 所经过的路线与直线
所经过的路线与直线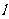 所围成的面积为
所围成的面积为
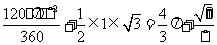 ;
;
第二次以 为旋转中心点
为旋转中心点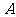 所经过的路线与直线
所经过的路线与直线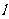 所围成的面积为
所围成的面积为
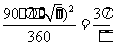 .
.
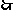 总面积为
总面积为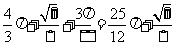 .
.
第25题. 经过旋转,图形上的每一点都绕 沿相同 转动了相同的 ,任意一对对应点与旋转中心的连线所成的角都是 ,对应点到 的距离相等.
答案:旋转中心 方向 角度 旋转角 旋转中心
第26题. 如图,它是由一个花瓣旋转 次,分别旋转 而得到的.

答案:3 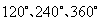
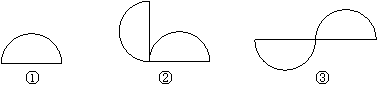
第27题. 如图所示,为一个风车的图形,其中一个图形是否为另一个图形经过旋转得来的?
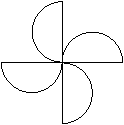
答案:解:(1)可由图形①旋转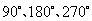 前后的图形构成;
前后的图形构成;
(2)可由图形②旋转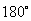 前后的图形构成;
前后的图形构成;
(3)可由图形③旋转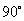 前后的图形构成.
前后的图形构成.
第28题. 如图,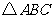 中,
中,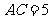 ,中线
,中线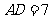 ,
,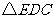 是由
是由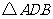 旋转
旋转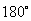 所得,则
所得,则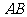 边的取值范围是( )
边的取值范围是( )
A.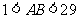 B.
B.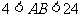
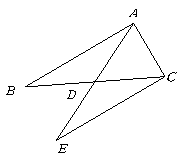 C.
C.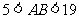 D.
D.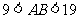
答案:D
第29题. 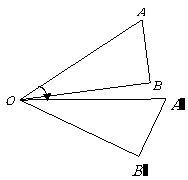 如图所示,
如图所示,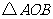 绕旋转中心
绕旋转中心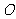 旋转
旋转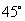 ,到
,到 ,那么
,那么
(1)点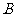 的对应点是点 .
的对应点是点 .
(2)点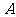 的对就点是点 .
的对就点是点 .
(3)线段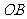 的对应线段是线段 .
的对应线段是线段 .
(4)线段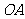 的对应线段是线段 .
的对应线段是线段 .
(5)线段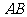 的对应线段是线段 .
的对应线段是线段 .
(6)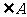 的对应角是 .
的对应角是 .
(7)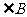 的对应角是 .
的对应角是 .
(8)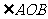 的对应角是 .
的对应角是 .
答案:(1) (2)
(2) (3)
(3)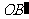 (4)
(4)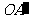 (5)
(5) (6)
(6)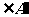 (7)
(7)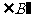 (8)
(8)
第30题. 如图,在下边的各组图案中,请你说出位置变化的名称.
(1)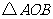 到
到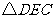 的位置变换叫做 .
的位置变换叫做 .
(2)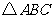 到
到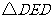 的位置变换叫做 .
的位置变换叫做 .
 (3)
(3) 和
和 的位置变换叫做 .
的位置变换叫做 .
答案:(1)平移 (2)轴对称 (3)旋转
第31题. 如图,是一个五叶风车的示意图,它可以看做是由“基本图案” 通过
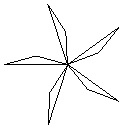 次旋转而得;若该风车在风中匀速旋转一周需
次旋转而得;若该风车在风中匀速旋转一周需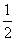 s,则经过
s,则经过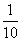 s,一个三角形叶片旋转了 度.
s,一个三角形叶片旋转了 度.
答案:一个三角形 5 72
第32题. 如图,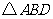 和
和 是等腰直角三角形,
是等腰直角三角形,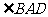 和
和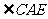 是直角,则图中可通过旋转而相互得到三角形是 ;旋转角为 度,旋转中心为 ,写出所有的对应线段 ,由此可知线段
是直角,则图中可通过旋转而相互得到三角形是 ;旋转角为 度,旋转中心为 ,写出所有的对应线段 ,由此可知线段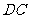 与
与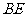 的位置关系为 .
的位置关系为 .

答案: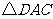 与
与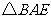 ,90,
,90,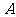 ,
,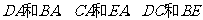 ,垂直
,垂直
第33题. 已知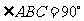 ,将
,将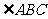 绕平面内一点
绕平面内一点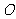 旋转
旋转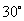 得到
得到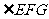 ,则
,则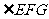 的度数为 .
的度数为 .
答案: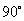
第34题. 正六边形可以看作是 形通过 次旋转图形,每次旋转 度,旋转方向是 .
答案:正三角形,5, ,逆时针或顺时针
,逆时针或顺时针
第35题. 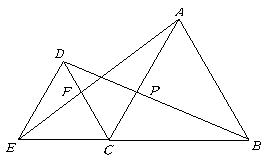 如图,
如图,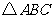 和
和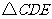 都是等边三角形,图中的三角形中,哪些三角形可以通过互相旋转得到?
都是等边三角形,图中的三角形中,哪些三角形可以通过互相旋转得到?
答案:
第36题. 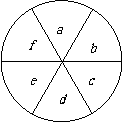 如图,转盘上有“
如图,转盘上有“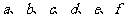 ”6个等格.
”6个等格.
①如果转盘顺时针旋转,字母“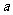 ”旋转 度时,才能得到字母“
”旋转 度时,才能得到字母“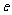 ”的位置,字母“
”的位置,字母“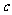 ”旋转 度时,才能转到字母 “
”旋转 度时,才能转到字母 “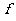 ”的位置.
”的位置.
②如果转盘逆时针旋转,字母“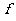 ”旋转 度时,才能转到字母“
”旋转 度时,才能转到字母“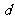 ”的位置.
”的位置.
答案:①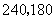 ②
②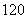
第37题. 在五边形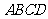 中,
中,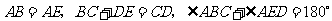 .
.
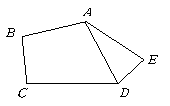 求证:
求证: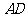 平分
平分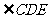 .
.
答案:解:连结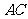 ,将
,将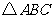 绕点
绕点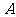 旋转
旋转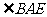 的度数到
的度数到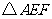 的位置.
的位置.
因为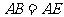 ,
,
所以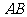 与
与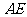 重合,
重合,
因为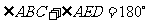 ,且
,且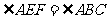 ,
,
所以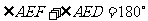 ,
,
所以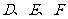 三点共交,
三点共交,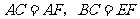 ,
,
在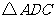 和
和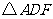 中,
中,
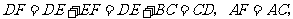
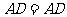
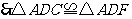 (SSS).
(SSS).
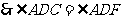 .
.
第38题. 如图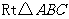 的边
的边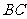 绕点
绕点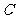 旋转到
旋转到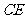 的位置,则下列说法正确的是( )
的位置,则下列说法正确的是( )
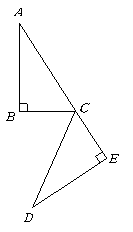 A.点
A.点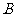 与点
与点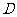 是对应点,则
是对应点,则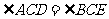 .
.
B.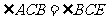
C.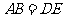
D.线段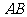 与线段
与线段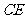 是对应线段
是对应线段
答案:C
第39题. 将如图所示的图案绕其中心旋转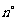 时与原图案完全重合,那么
时与原图案完全重合,那么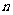 的最小值是( )
的最小值是( )
A.60 B.90 C.120 D.180
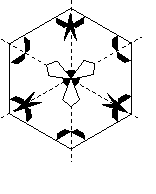
答案:C
3.1旋转(2)
第1题. 任画一个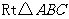 ,其中
,其中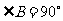 ,分别作出
,分别作出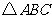 按如下条件旋转后或平移后的图形.(1)取三角形外一点
按如下条件旋转后或平移后的图形.(1)取三角形外一点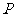 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转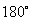 .
.
(2)将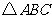 平移,使得
平移,使得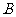 点的对应点为
点的对应点为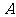 点.
点.
答案:解:(1)如图,分别连结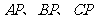 并延长到
并延长到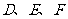 ,使
,使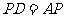 ,
,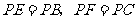 ,连结
,连结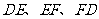 ,则
,则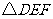 就是以点
就是以点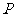 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转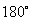 后的三角形.
后的三角形.
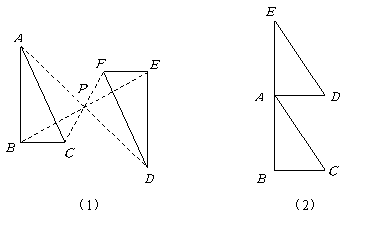 (2)如图,按照
(2)如图,按照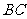 的方向作射线
的方向作射线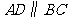 ,在射线
,在射线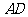 上截取线段
上截取线段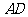 ,使
,使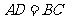 ,延长
,延长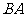 到
到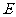 ,使
,使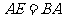 ,连结
,连结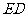 ,则
,则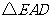 就是
就是 平移后的三角形.
平移后的三角形.
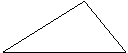
第2题. 已知,如图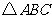 为直角三角形,且
为直角三角形,且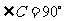 ,点
,点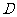 是
是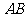 的中点,
的中点,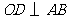 ,并且
,并且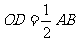 .
.
(1)试画出将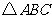 绕点
绕点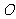 按顺时针方向连续旋转三次,每次旋转
按顺时针方向连续旋转三次,每次旋转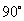 的图形.
的图形.
|
 |
|||||
|
|||||
 |
|||||
|
 答案:解:(1)连续旋转三次每次旋转
答案:解:(1)连续旋转三次每次旋转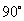 所得图形;
所得图形;
(2)如图,设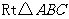 中,
中,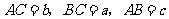 ,
,
则可证四边形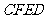 为正方形.又可证四边形
为正方形.又可证四边形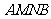 为一边长为
为一边长为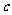 的小正
的小正
方形.故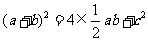 .化简得
.化简得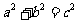 .
.
第3题. 在旋转的过程中,确定一个三角形旋转后的位置,除需要此三角形原来的位置外,还需要的条件是 .
答案:旋转中心、旋转角
第4题. 如图,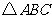 是直角三角形,
是直角三角形,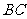 为斜边,将
为斜边,将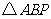 绕点
绕点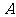 逆时针旋转后,能与
逆时针旋转后,能与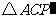 重合,若
重合,若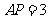 ,求
,求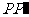 的长.
的长.

答案:
第5题. 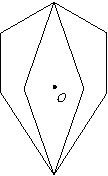 如何作出图中的图案绕
如何作出图中的图案绕 点按顺时针方向旋转
点按顺时针方向旋转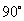 后的图形.
后的图形.
答案:略
第6题.  如图,
如图,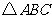 以
以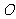 为旋转中心,旋转
为旋转中心,旋转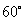 ,请作出旋转后的图形.
,请作出旋转后的图形.
答案:提示:确定旋转角
第7题. 将图中的图形绕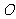 点按顺时针方向旋转
点按顺时针方向旋转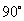 ,作出旋转后的图形.
,作出旋转后的图形.
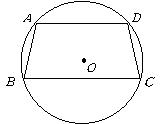
答案:提示:主要作出梯形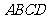 旋转后的图形
旋转后的图形

第8题. .如图,若将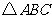 绕点
绕点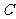 顺时针旋转
顺时针旋转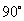 后得到
后得到
 ,则
,则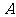 点的对应点
点的对应点 的坐标是( )
的坐标是( )
A.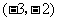 B.
B.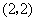
C.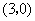 D.
D.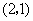
答案:C
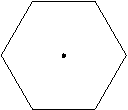 第9题. 绕一定点旋转
第9题. 绕一定点旋转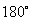 后能与原来图形重合的图形是中心对称
后能与原来图形重合的图形是中心对称
图形,正六边形就是这样的图形.小明发现将正六边形绕着它的中
心旋转一个小于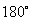 的角,也可以使它与原来的正六边形重合.请
的角,也可以使它与原来的正六边形重合.请
你写出小明发现的一个旋转角的度数: .
答案: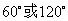
第10题.  如图,四边形
如图,四边形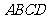 绕
绕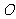 点旋转后,顶点
点旋转后,顶点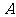 的对应点为
的对应点为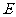 ,试确定
,试确定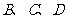 对应点的位置,以及旋转后的四边形.
对应点的位置,以及旋转后的四边形.
答案:解:(1)连结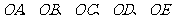 ;
;
(2)分别以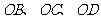 为一边作
为一边作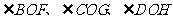 ,
,
使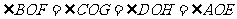 ;
;
(3)分别在射线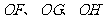 上,截取
上,截取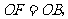
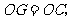
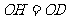 ;
;
(4)连结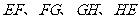 .
.
因此四边形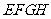 就是所求,如图.
就是所求,如图.

第11题. 如图,是某设计师设计的方桌布图案的一部分,请你运用旋转变换的方法,在坐标纸上将该图形绕原点顺时针依次旋转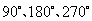 ,并画出它在各象限内的图形,你会得到一个美丽的立体图形,你来试一试吧!但是涂阴影时要注意利用旋转变换的特点,不要涂错了位置.否则不会出现理想的效果,并且还要扣分噢!
,并画出它在各象限内的图形,你会得到一个美丽的立体图形,你来试一试吧!但是涂阴影时要注意利用旋转变换的特点,不要涂错了位置.否则不会出现理想的效果,并且还要扣分噢!
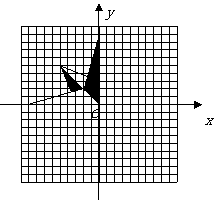
 答案:解:所画图形如图所示.
答案:解:所画图形如图所示.
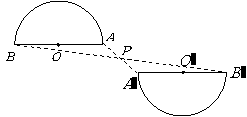
第12题. 如图,半圆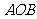 绕
绕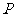 点旋转后,直径
点旋转后,直径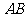 端点
端点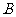 的对应点为
的对应点为 ,试确定:
,试确定:
(1)点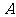 的对应点
的对应点 以及旋转后的半圆;
以及旋转后的半圆;
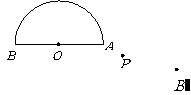 (2)若不先确定
(2)若不先确定 ,能否作图?
,能否作图?
答案:解:(1)如图.
①连结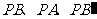 ;
;
②以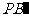 为边作
为边作 ;
;
③在射线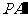 上取
上取 ;
;
④连结 ,在
,在 上取
上取 点有
点有 ;
;
⑤以 为圆心,
为圆心,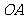 为半径作半圆弧.
为半径作半圆弧.
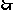 半圆
半圆 就是半圆
就是半圆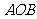 绕
绕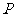 点旋转后的图形.
点旋转后的图形.
(2)若不确定 点,也可以作图,方法如下:
点,也可以作图,方法如下:
①连结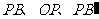 ;
;
②以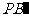 为边作
为边作 且有
且有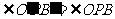 ;
;
③以射线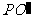 上取
上取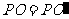 ;
;
④以 为圆心,
为圆心, 长为半径作弧与
长为半径作弧与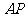 延长线交于
延长线交于 点.
点.
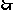 半圆
半圆 就是半圆
就是半圆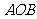 绕
绕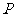 点旋转后的图形.
点旋转后的图形.
第13题. 在旋转作图中,首先要确定 的位置,然后要知道旋转 和旋转 .
答案:图形原来 中心 角
第14题. 旋转作图中,常用的基本作图是 .
答案:作一条线段等于已知线段,作一个角等于已知角
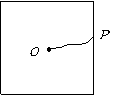
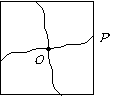
第15题. 如图,过正方形的中心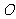 点和边上一点
点和边上一点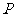 随意画一条曲线,将所画的曲线绕
随意画一条曲线,将所画的曲线绕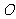 点按同一方向连续旋转三次,每次的旋转角度都是
点按同一方向连续旋转三次,每次的旋转角度都是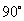 ,这样就将正方形分成四部分,这四部分之间有什么关系?
,这样就将正方形分成四部分,这四部分之间有什么关系?
 `
`
答案:解:这四部分是大小、形状完全相同的四块图案.
第16题. 如图,如果四边形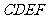 旋转后能与正方形
旋转后能与正方形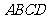 重合,那么图形所在的平面上可以看作旋转中心的有 个.
重合,那么图形所在的平面上可以看作旋转中心的有 个.
答案:3
20.( 10分)某校初三学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
|
|
1号 |
2号 |
3号 |
4号 |
5号 |
总数 |
|
甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
|
乙班 |
89 |
100 |
95 |
119 |
97 |
500 |
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.
请你回答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)估计两班比赛数据的方差哪一个小?
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
19.(10分)
某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
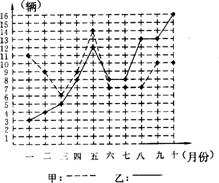
(1)请你根据上图填写下表:
|
销售公司 |
平均数 |
方差 |
中位数 |
众数 |
|
甲 |
|
|
9 |
|
|
乙 |
9 |
17.0 |
|
8 |
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).
8.90 8.75 8.90 8.95 8.80 8.85
问这组数据中的中位数和众数以及去掉一个最高分和一个最低分后的平均分分别是多少?
8.70 8.80 8.80 8.60 8.85 9.00
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com