
题目列表(包括答案和解析)
1.4的平方根是( )
A.2
B.±2 C.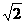 D.±
D.±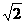
3.(本题8分)
某校八年级学生开展踢毽子比赛活动,每班派5名学生参加.按团体总分多少排列名
次。在规定时间每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名
 学生的比赛数据(单位:个)
学生的比赛数据(单位:个)
请你回答下列问题:
(1)填写表格;
(2)根据以上信息,请你回答下列问题:
①从平均数、众数相结合的角度分析,应该把冠军奖状发给哪一个班级?
②从优秀率的角度分析,应该把冠军奖状发给哪一个班级?
(3)如果两个班各选两名同学参加市踢毽子的比赛,你认为哪个班级团体实力更强?
为什么?


2.(本题8分)
如图13,是一个反比例函数图像的一部分,点A(1,l0),B(10,1)是它的端点.
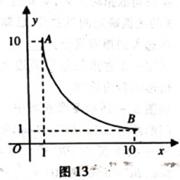 (1)求此函数的解析式,并写出自变量茗的取值范围;
(1)求此函数的解析式,并写出自变量茗的取值范围;
(2)请你举出一个能用本题的函数关系描述的生活实例.
1.(本题8分)
玉树大地震发生以后,全国人民众志成城.首长到帐篷厂视察,布置赈灾生产任务,下
面是首长与厂长的一段对话:
首长:为了支援灾区人民,组织上要求你们完成12000顶帐篷的生产任务.
厂长:为了尽快支援灾区人民,我们准备每天的生产量比原来提高50%.
首长:这样能提前几天完成任务?
厂长:请首长放心!保证提前4天完成任务!
根据两人对话,问该厂原来每天生产多少顶帐篷?
2.(本题10分)
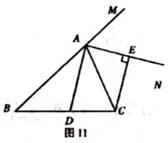 已知:如图11,在△ABC中,AD平分
已知:如图11,在△ABC中,AD平分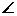 BAC,AN是△ABC外角
BAC,AN是△ABC外角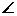 CAM的平分线,CE
CAM的平分线,CE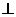 AN,垂足为点E.
AN,垂足为点E.
(1)猜想四边形ADCE形状,并加以证明;
(2)如图12,若添加“AB=AC”,其他条件不变,求证:四边形ADCE为矩形;
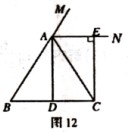
(3)在(2)的条件下,当△ABC满足什么条件时,四边形ADCE是一个正方形?(只需
写出条件,不需证明)
1.(本题8分)
在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.李颖同学按照取两组对边中
点的方法折出菱形EFGH(见方案一);张丰同学沿矩形的对角线AC折出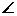 CAE=
CAE=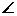 DAC,
DAC,
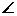 ACF=
ACF=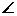 ACB的方法得到菱形AECF(见方案二),如图l0.请你通过计算,比较李颖同学
ACB的方法得到菱形AECF(见方案二),如图l0.请你通过计算,比较李颖同学
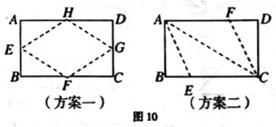 和张丰同学的折法中,哪种菱形面积较大?
和张丰同学的折法中,哪种菱形面积较大?
解答题(本大题共3个小题;每小题6分,共18分)
(1)计算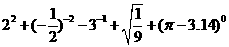 .
.
(2)先化简,再求值: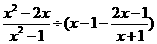 ,其中
,其中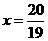 .
.
(3)解方程: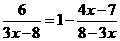 .
.
10.如图9所示,已知M是平行四边形ABCD的AB边的中点,CM交BD于点E,BD=
3BE,则图中阴影部分面积与平行四边形ABCD面积之比为____________。
9.下列图形:①线段;②矩形;③菱形;④正方形;⑤等边三角形.绕其重心旋转180°后,仍与原图形完全重合的有____________
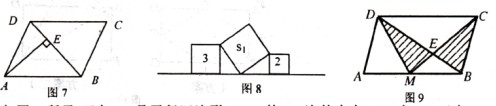
8.如图8,一条直线上依次摆放着三个正方形.已知斜着放置的一
个正方形的面积为s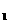 ,正着放置的两个正方形的面积分别为3、2, 则s
,正着放置的两个正方形的面积分别为3、2, 则s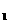 =_________。
=_________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com