
题目列表(包括答案和解析)
4.在19进10的比赛中,19位选手的得分互不相同.选手甲在得知自己的成绩后,想要
判断自己能否进入前10名,只需知道所有选手成绩的
A.平均数 B.中位数
C.众数 D.总和
3.化简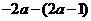 所得的结果是
所得的结果是
A.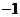 B.
B.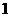
C.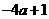 D.
D.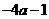
2.在平面直角坐标系中,点P(4,6)在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
1.2的绝对值是
A.-2
B.2
C.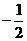 D.
D.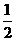
24、(8分) 解:(1)△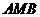 ≌△
≌△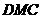 ;△
;△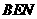 ≌△
≌△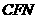 2分
2分
(2)判断四边形MENF为菱形; 3分
证明:∵ABCD为等腰梯形,
∴AB=CD,∠A=∠D , 又∵M为AD的中点, ∴MA=MD
∴△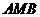 ≌△
≌△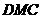 ,∴BM=CM ; 4分
,∴BM=CM ; 4分
又∵E、F、N分别为BM、CM、BC中点,
∴MF=NE=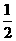 MC,ME=NF=
MC,ME=NF=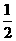 BM ,(或MF∥NE, ME∥NF ;) 5分
BM ,(或MF∥NE, ME∥NF ;) 5分
∴EM=NF=MF=NE;
∴四边形MENF为菱形. 6分
(说明:第(2)问判断四边形MENF仅为平行四边形,并正确证明的只给3分.)
(3)当h=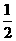 BC(或BC=2h或BC=2MN)时,MENF为正方形. 8分
BC(或BC=2h或BC=2MN)时,MENF为正方形. 8分
23、(本题满分7分)
(1)把M(2,3)代入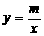 得
得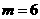 ,所以
,所以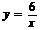 (1分)
(1分)
把M(2,3)代入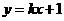 得
得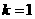 ,所以
,所以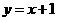 (2分)
(2分)
(2)由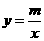 和
和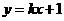 的图像性质得,N(―3,―2)(2分)
的图像性质得,N(―3,―2)(2分)
(3)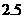 (2分)
(2分)
22、(7分)答:
(1)这10名男生立定跳远成绩的极差为0.73和平均数为2.25;
(2)这10名男生立定跳远得分的中位数为2.29和众数为;
(3)如果将9分(含9分)以上定为“优秀”,估计这480名男生中得优秀的人数为288人.
21、(6分)
解:设王老师步行的速度是x千米/时,则骑自行车的速度是3x千米/时, 20分钟=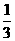 小时,由题意,得
小时,由题意,得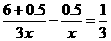 ,解得x=5.
,解得x=5.
经检验x=5是所列方程的根,∴3x=3×5=15(千米/时).
答:王老师步行的速度是5千米/时,骑自行车的速度是15千米/时。
20、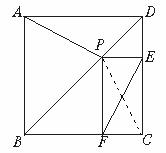 (5分)
(5分)
解:连结PC。
∵四边形ABCD是正方形,
∴AD=DC,∠ADP=∠CDP,
∵PD=PD,
∴△APD≌△CPD,
∴AP=CP
∵四边形ABCD是正方形,∴∠DCB=90°,
∵PE⊥DC,PF⊥BC,∴四边形PFCE是矩形
∴PC=EF。
 ∵∠DCB=90°,
∵∠DCB=90°,
∴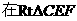 中,
中,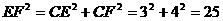 ,
,
∴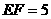 ,
,
∴AP=CP=EF=5。(其它方法证明也一样得分)
20、(5分)如图,连接DB,

(其它方法证明也一样得分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com