
题目列表(包括答案和解析)
7,反比例函数y=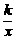 的图象经过点(-2,-1),那么k的值为_________.
的图象经过点(-2,-1),那么k的值为_________.
8,已知y与2x-1成反比例,且当x=1时,y=2,那么当x=0时,y=________.
9,如果点(a,-2a)在函数y=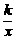 的图象上,那么k______0.(填“>”或“<”)
的图象上,那么k______0.(填“>”或“<”)
10,对于函数y=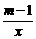 ,当m 时,y是x的反比例函数,且比例系数是3.
,当m 时,y是x的反比例函数,且比例系数是3.
11,通过画图我们可以发现一次函数y=2x-1与反比例函数y=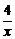 的图象交点的个数为___个.
的图象交点的个数为___个.
12,(08芜湖市)在平面直角坐标系 中,直线
中,直线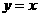 向上平移1个单位长度得到直线
向上平移1个单位长度得到直线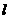 .直线
.直线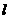 与反比例函数
与反比例函数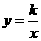 的图象的一个交点为
的图象的一个交点为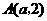 ,则
,则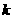 的值等于
.
的值等于
.
1,下列关系式:(1)y=-x;(2)y=2x-1;(3)y=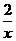 ;(4)y=
;(4)y=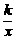 (k>0).其中y是x的反比例函数的有( )
(k>0).其中y是x的反比例函数的有( )
A.1个 B.2个 C.3个 D.4个
2,反比例函数y=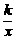 (k≠0)中自变量的范围是( )
(k≠0)中自变量的范围是( )
A. x≠0 B.x=0 C.x≠1 D.x=-1
3,下列函数中,y与x成反比例函数关系的是( )
A.x(y-1)=1
B. y=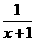 C. y=
C. y=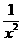 D. y=
D. y=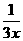
4,如果双曲线y=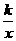 过点A(3,-2),那么下列各点在双曲线上的是( )
过点A(3,-2),那么下列各点在双曲线上的是( )
A.(2,3) B.(6,1) C.(-1,-6) D.(-3,2)
5,若变量y与x成正比例,变量x又与z成反比例,则y与z的关系是( )
A.成反比例 B.成正比例 C.y与z2成正比例 D.y与z2成反比例
6,已知P为函数y=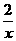 图像上一点,且P到原点的距离为2,则符合条件的点P数为( )
图像上一点,且P到原点的距离为2,则符合条件的点P数为( )
A.0个 B.2个 C.4个 D.无数个
13,反比例函数的图象过点(2,-2),求函数y与自变量x之间的关系式,它的图象在第几象限内?y随x的减小如何变化?请画出函数图象,并判断点(-3,0),(-3,-3)是否在图象上?
14,若反比例函数y=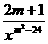 的图象经过第二、四象限,求函数的解析式.
的图象经过第二、四象限,求函数的解析式.
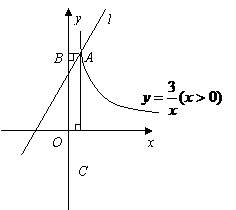
15,如图3所示,一个反比例函数的图象在第二象限内,点A是图象上的任意一点,AM⊥x轴于M,O是原点,若S△AOM=3,求该反比例函数的解析式,并写出自变量的取值范围.
16,点P,Q在y=-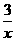 的图象上.
的图象上.
(1)若P(1,a),Q(2,b),比较a,b的大小;
(2)若P(-1,a),Q(-2,b),比较a,b的大小;
(3)你能从中发现y随x增大时的变化规律吗?
(4)若P(x1,y1),Q(x2,y2),x1<x2,你能比较y1与y2的大小吗?
17,(08达州市)平行于直线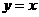 的直线
的直线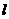 不经过第四象限,且与函数
不经过第四象限,且与函数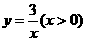 和图象交于点
和图象交于点 ,过点
,过点 作
作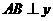 轴于点
轴于点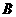 ,
,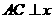 轴于点
轴于点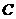 ,四边形
,四边形 的周长为8.求直线
的周长为8.求直线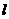 的解析式.
的解析式.
18,已知变量y与x成反比例,并且当x=2时,y=-3.
(1)求y与x的函数关系式;
(2)求当y=2时x的值;
(3)在直角坐标系内画出(1)小题中函数图象的草图.
7,已知反比例函数y=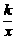 (k≠0)与一次函数y=x的图象有交点,则k的范围是______.
(k≠0)与一次函数y=x的图象有交点,则k的范围是______.
8,已知反比例函数y=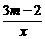 ,当m___时,其图象的两个分支在第二、四象限内;当m___时,其图象在每个象限内y随x的增大而减小.
,当m___时,其图象的两个分支在第二、四象限内;当m___时,其图象在每个象限内y随x的增大而减小.
9,若反比例函数y=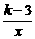 的图象位于一、三象限内,正比例函数y=(2k-9)x过二、四象限,则k的整数值是______.
的图象位于一、三象限内,正比例函数y=(2k-9)x过二、四象限,则k的整数值是______.
10,已知点P(1,a)在反比例函数y=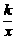 (k≠0)的图象上,其中a=m2+2m+3(m为实数),则这个函数的图象在第______象限.
(k≠0)的图象上,其中a=m2+2m+3(m为实数),则这个函数的图象在第______象限.
11,写出一个反比例函数,使它的图象在第二、 四象限,这个函数的解析式是_____.
12,已知反比例函数y=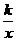 (k≠0),当x>0时,y随x的增大而增大,那么一次函数y=kx-k的图像过 象限.
(k≠0),当x>0时,y随x的增大而增大,那么一次函数y=kx-k的图像过 象限.
1,点A(-2,y1)与点B(-1,y2)都在反比例函数y=-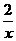 的图像上,则y1与y2的大小关系为( )
的图像上,则y1与y2的大小关系为( )
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
2,若点(3,4)是反比例函数y=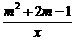 图象上一点,则此函数图象必经过点( )
图象上一点,则此函数图象必经过点( )
A.(2,6) B.(2,-6) C.(4,-3) D.(3,-4)
3,在函数y=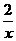 ,y=x+5,y=-5x的图像中,是中心对称图形,且对称中心是原点的图像的个数有( )
,y=x+5,y=-5x的图像中,是中心对称图形,且对称中心是原点的图像的个数有( )
A.0 B.1 C.2 D.3
4,已知函数y=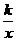 (k<0),又x1,x2对应的函数值分别是y1,y2,若x2>x1>0对,则有( )
(k<0),又x1,x2对应的函数值分别是y1,y2,若x2>x1>0对,则有( )
A.y1>y2>0 B.y2>y1>0 C.y1<y2<0 D.y2<y1<0
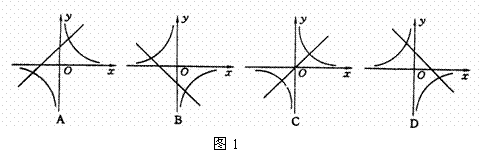
5,如图1,函数y=a(x-3)与y=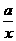 ,在同一坐标系中的大致图象是( )
,在同一坐标系中的大致图象是( )
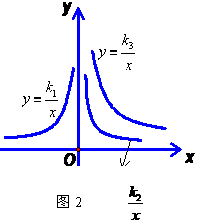
6,如图2是三个反比例函数y=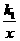 ,y=
,y=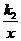 ,y=
,y=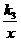 在x轴上方的图象,由此观察k1、 k2、k3得到的大小关系为( )
在x轴上方的图象,由此观察k1、 k2、k3得到的大小关系为( )
A.k1>k2>k3 B.k2>k3>k1 C.k3>k2>k1 D.k3>k1>k2
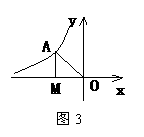
15.解:(1) 点
点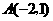 在反比例函数
在反比例函数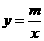 的图象上,
的图象上,
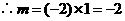 .
. 反比例函数的表达式为
反比例函数的表达式为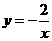 .
.
 点
点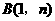 也在反比例函数
也在反比例函数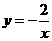 的图象上,
的图象上,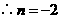 ,即
,即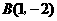 .
.
把点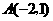 ,点
,点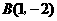 代入一次函数
代入一次函数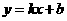 中,得
中,得
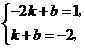 解得
解得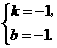
 一次函数的表达式为
一次函数的表达式为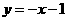 .
.
(2)在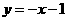 中,当
中,当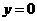 时,得
时,得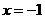 .
. 直线
直线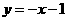 与
与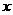 轴的交点为
轴的交点为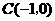 .
.
 线段
线段 将
将 分成
分成 和
和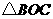 ,
,
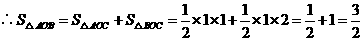 .
.
14. (1)由已知设交点A(m,6)
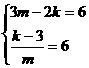
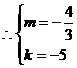
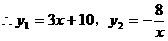
(2)由方程组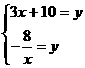 得
得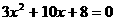
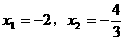
由图像可知当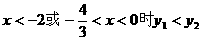
13.(1)把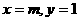 代入
代入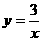 ,
,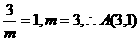 ,把
,把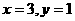 代入
代入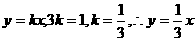 ,(2)解方程组
,(2)解方程组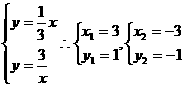 ,故另一交点为(-3,-1);
,故另一交点为(-3,-1);
12. (1)反比例函数,y=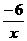 .(2)该函数性质如下:
.(2)该函数性质如下:
①图象与x轴、y轴无交点;
②图象是双曲线,两分支分别位于第二、四象限;
③图象在每一个分支都朝右上方延伸,当x<0时,y随x的增大而增大,当x>0时,y随x的增大而增大.
1. 双曲线,2,二、四,提示:因为-4<0,所以图象位于二、四象限;2.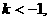 提示:由图象两支分布在第二、四象限内得到
提示:由图象两支分布在第二、四象限内得到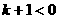 ,即
,即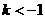 ;3.-6;4.B,提示:先求出反比例函数的解析式为
;3.-6;4.B,提示:先求出反比例函数的解析式为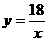 ,将选项代入解析式,正确的是B;5.C,提示:又-1<0,图象位于二、四象限,又因为
,将选项代入解析式,正确的是B;5.C,提示:又-1<0,图象位于二、四象限,又因为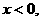 所以图象位于第二象限,故选C;6. .y2<y3<y1,提示:根据反比例函数的性质得到;7. 图①,理由是:粮食产量a必为正数,故其图象应在第一、三象限.人口数量x也为正数,故图象必在第一象限,又xy=a,则其图象应为双曲线的一个分支,综上,可知y与x的函数图象必为图①.;8. y=-
所以图象位于第二象限,故选C;6. .y2<y3<y1,提示:根据反比例函数的性质得到;7. 图①,理由是:粮食产量a必为正数,故其图象应在第一、三象限.人口数量x也为正数,故图象必在第一象限,又xy=a,则其图象应为双曲线的一个分支,综上,可知y与x的函数图象必为图①.;8. y=-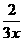 ;9. y=
;9. y=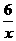 ,提示:设A点的坐标(
,提示:设A点的坐标(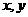 ),根据三角形的面积得
),根据三角形的面积得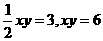 ,所以反比例函数的比例系数为
,所以反比例函数的比例系数为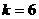 ,所以
,所以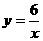 ;10.C;11.D;
;10.C;11.D;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com