
题目列表(包括答案和解析)
6.如果y=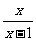 ,那么用y的代数式表示x为( )
,那么用y的代数式表示x为( )
A. 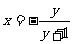 B.
B. 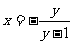 C.
C. 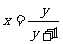 D.
D. 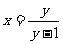
5.化简x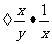 等于( )
等于( )
A.1
B.xy
C.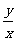 D.
D.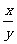
4.已知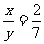 ,则
,则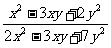 的值是( )
的值是( )
A.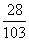 B.
B.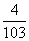 C.
C.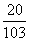 D.
D.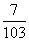
3.已知a-b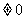 ,且2a-3b=0,则代数式
,且2a-3b=0,则代数式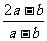 的值是( )
的值是( )
A.-12 B.0 C.4 D.4或-12
2.下列分式运算,结果正确的是( )
A.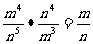 ; B.
; B.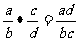 C .
C . 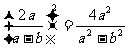 ; D.
; D.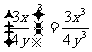
1.下列运算正确的是( )
A.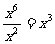 B.
B.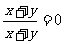 C.
C.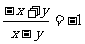 D.
D.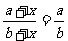
16.2.2分式的加减(二)
|
教学目标 |
明确分式混合运算的顺序,熟练地进行分式的混合运算. |
|
重点、难点 |
重点:熟练地进行分式的混合运算. |
|
难点:熟练地进行分式的混合运算. |
|
|
情感态度与价值观 |
通过学习课堂知识使学生懂得任何事物之间是相互联系的,理论来源于实践,服务于实践。能利用事物之间的类比性解决问题。 |
教 学 过 程
|
教学设计
与 师生互动 |
备
注 |
|
第一步:课堂引入 提问:1.说出分数混合运算的顺序. 2.教师指出分数的混合运算与分式的混合运算的顺序相同. 类比: 分式混合运算时,要注意运算顺序, 在没有括号的情况下,按从左到右的方向,先乘方,再乘除,然后加减. 有括号要按先小括号,再中括号,最后大括号的顺序.混合运算后的结果分子、分母要进行约分, 注意最后的结果要是最简分式或整式.分子或分母的系数是负数时,要把“-”号提到分式本身的前面. 说明:分式的加、减、乘、除混合运算注意以下几点: (1)一般按分式的运算顺序法则进行计算,但恰当地使用运算律会使运算简便。 (2)要随时注意分子、分母可进行因式分解的式子,以备约分或通分时备用,可避免运算烦琐。 (3)注意括号的“添”或“去”、“变大”与“变小”。 (4)结果要化为最简分式。 |
|
|
第二步;例题讲解 (P21)例8.计算 [分析] 这道题是分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序:先乘方,再乘除,然后加减,最后结果分子、分母要进行约分,注意运算的结果要是最简分式. (补充)计算 (1) 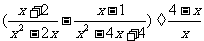 [分析] 这道题先做括号里的减法,再把除法转化成乘法,把分母的“-”号提到分式本身的前边.. 解: 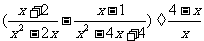 = 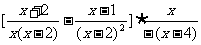 = 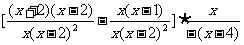 = 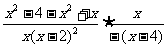 = 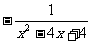 (2) 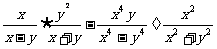 [分析] 这道题先做乘除,再做减法,把分子的“-”号提到分式本身的前边. 解:  = 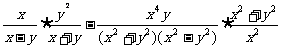 = 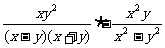 = 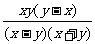 =  [例1]计算:(1)[ 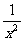 + +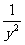 + +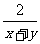 ( (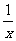 + +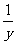 )]· )]·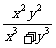 ; ;(2)(x-y- 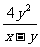 )(x+y- )(x+y-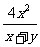 )÷[3(x+y)- )÷[3(x+y)-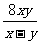 ]。 ]。分析:分式的四则混合运算要注意运算顺序及括号的关系。 解:(1)原式=[ 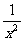 + +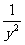 + +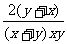 ]· ]·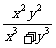 =[ 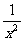 + +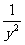 + +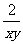 ]· ]·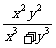 = 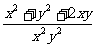 · ·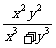 = 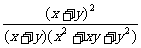 = =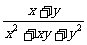 。 。(2)原式= 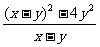 · ·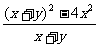 ÷ ÷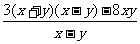 = 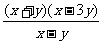 · ·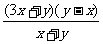 · ·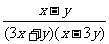 =y-x。 [例2]计算:(1)( 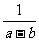 - -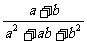 + +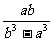 )·(a3-b3); )·(a3-b3);(2)( 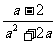 - -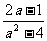 )÷ )÷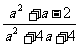 。 。解:(1)原式= 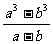 - -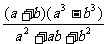 + + = 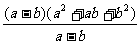 - -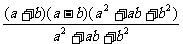 +ab +ab=a2+ab+b2-(a2-b2)-ab = a2+ab+b2-a2+b2-ab =2b2。 (2)原式=[ 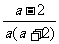 - -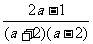 ]· ]·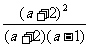 = 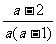 - -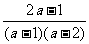 = =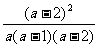 - -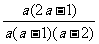 = 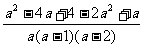 = =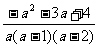 = 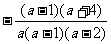 = =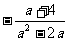 。 。[例]已知x+ 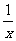 =3,求下列各式的值: =3,求下列各式的值:(1)x2+ 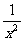 ; (2)x3+ ; (2)x3+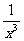 ;(3) ;(3)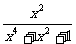 。 。分析:观察已知条件和所求式,可将所求的式进行分解因式,将已知条件整体代入,第(3)题是先求它的倒数值,可以将x2+ 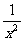 =7直接代入,求得它的值。此外对于已知条件x+ =7直接代入,求得它的值。此外对于已知条件x+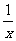 =3,可以变形为x2-3x+1=0,也可以变形为 =3,可以变形为x2-3x+1=0,也可以变形为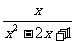 =1,在后两种表达形式下,要能熟练地将它转化为x+ =1,在后两种表达形式下,要能熟练地将它转化为x+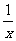 =3。 =3。解:(1)x2+ 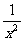 =(x+ =(x+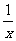 )2-2=32-2=7; )2-2=32-2=7;(2)x3+ 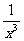 =(x+ =(x+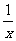 )( x2-1+ )( x2-1+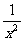 ) )=3×(7-1)=18; (3)∵ 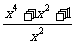 = x2+ = x2+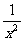 +1=7+1=8, +1=7+1=8,∴  = =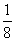 |
|
|
第三步;随堂练习 计算 (1) 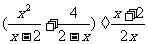 (2) (2)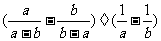 (3) 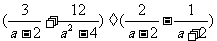 .答案:(1)2x (2) 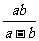 (3)3 (3)3 |
|
|
第四步:课后练习 1.计算 (1) 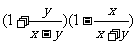 (2) 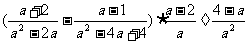 (3) 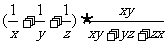 2.计算 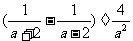 ,并求出当 ,并求出当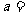 -1的值 -1的值答案:1.(1) 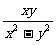 (2) (2)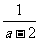 (3) (3)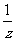 2. 2.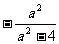 ,- ,-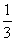 创新能力运用 1.已知:x+y+z=3y=2z,求 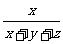 的值。 的值。2.已知: 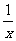 - -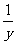 =3,求 =3,求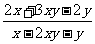 的值。 的值。 |
|
|
课后小结 : |
|
|
课后反思: |
15.先化简,再求值: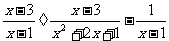 ,其中x=
,其中x=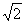 +1.
+1.
14.先化简,再求值: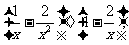 其中x=-3.5.
其中x=-3.5.
13.化简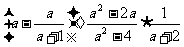 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com