
题目列表(包括答案和解析)
5. 当
≥ 时,一元二次方程
时,一元二次方程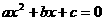 的求根公式为
。
的求根公式为
。
4、 用配方法解方程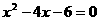 ,则
,则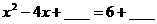 ,
,
所以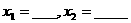 。
。
3. 方程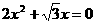 的根是
。
的根是
。
2、 比较大小: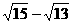 _____
_____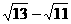 ;
; 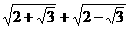 _____
_____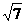 。
。
1、 关于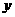 的一元二次方程
的一元二次方程 的一般形式是
。
的一般形式是
。
25.(12分)如图,在一块三角形区域ABC中,∠C=90°,边AC=8,BC=6,现要在△ABC内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上。
⑴求△ABC中AB边上的高h;
⑵设DG=x,当x取何值时,水池DEFG的面积最大?
 ⑶实际施工时,发现在AB上距B点1.85的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果在,为保护大树,请设计出另外的方案,使三角形区域中欲建的最大矩形水池能避开大树。
⑶实际施工时,发现在AB上距B点1.85的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果在,为保护大树,请设计出另外的方案,使三角形区域中欲建的最大矩形水池能避开大树。
24、(12分)已知抛物线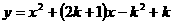 .
(1)求证:此抛物线与x轴总有两个不同的交点;
(2)设x1、x2是此抛物线与x轴两个交点的横坐标,且满足
.
(1)求证:此抛物线与x轴总有两个不同的交点;
(2)设x1、x2是此抛物线与x轴两个交点的横坐标,且满足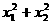 =
=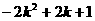 .
①求抛物线的解析式;
②设点P(m1,n1)、Q(m2,n2)是抛物线上两个不同的点,且关于此抛物线的对称轴对称,求m1+m2的值.
.
①求抛物线的解析式;
②设点P(m1,n1)、Q(m2,n2)是抛物线上两个不同的点,且关于此抛物线的对称轴对称,求m1+m2的值.
23.(12分)某商人如果将进货价为8元的商品按每件10元出售,每天可销售100件,现采用提高售出价,减少进货量的办法增加利润,已知这种商品每涨价1元其销售量就要减少10件,问他将售出价定为多少元时,才能使每天所赚的利润最大?并求出最大利润.
22、(10分)已知抛物线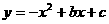 与x轴的两个交点分别为A(
与x轴的两个交点分别为A(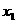 ,0),B(
,0),B(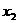 ,0),且
,0),且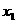 +
+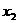 =4,
=4,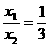 。 (1)求此抛物线的解析式;(2)设此抛物线与y轴的交点为C,过点B、C作直线,求此直线的解析式;(3)求△ABC的面积.
。 (1)求此抛物线的解析式;(2)设此抛物线与y轴的交点为C,过点B、C作直线,求此直线的解析式;(3)求△ABC的面积.
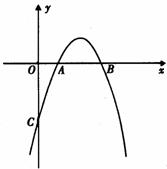
21.已知抛物线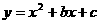 与
与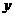 轴交于点A,与
轴交于点A,与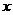 轴的正半轴交于B、C两点,且BC=2,S△ABC=3,则
轴的正半轴交于B、C两点,且BC=2,S△ABC=3,则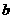 = ,
= ,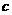 = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com