
题目列表(包括答案和解析)
6.函数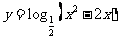 的单调递减区间是
的单调递减区间是
A. B.
B. C.
C. D.
D.
5.设方程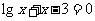 的实数根为
的实数根为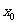 ,则
,则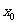 所在的一个区间是
所在的一个区间是
A. B.
B.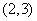 C.
C.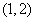 D.
D.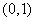
4.已知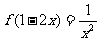 ,那么
,那么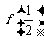 =
=
A.4
B.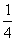 C.16 D.
C.16 D.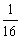
3.设函数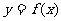 的图象关于原点对称,则下列等式中一定成立的是
的图象关于原点对称,则下列等式中一定成立的是
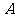 .
.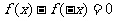 B.
B.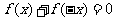 [
[
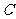 .
.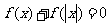
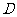 .
.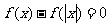
1下列说法错误的是
A.如果图象不间断的函数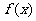 满足
满足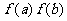 <0,则
<0,则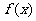 在区间(a,b)上至少存在一个零点.
在区间(a,b)上至少存在一个零点.
B.连续不间断的函数的零点的近似值都可以用"二分法"求。
C.按照二分法的步骤进行反复计算,则计算次数越多,所得零点就越精确
D.在用二分法求函数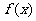 零点近似值时,所取的第一个区间(a,b)必须满足
零点近似值时,所取的第一个区间(a,b)必须满足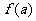
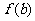 <0
<0
2.用“辗转相除法”求得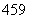 和
和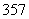 的最大公约数是
的最大公约数是
A 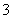 B
B 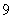 C
C 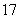 D
D 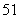
22.(本小题满分14分)
已知某海滨浴场的海浪高度y(米)是时间t(0≤t≤24单位小时)的函数,记作:y=f(t).下表是
某日各时的浪高数据;
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
1.5 |
1.0 |
0.5 |
1.0 |
1.5 |
1 |
0.5 |
0.99 |
1.5 |
经长期观测,y=f(t).的曲线可近似地看成是函数y=Acosωt +b
(1).根据以上数据,求出函数y=Acosωt +b的最小正周期T,振幅A及函数表达式;
(2).根据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断
一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行活动?
20. (本小题满分13分)
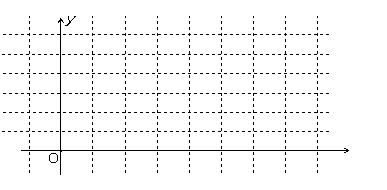
设函数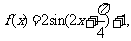 (1)用五点法画出它在一个周期内的闭区间上的图象;(2)说明此函数图象可由
(1)用五点法画出它在一个周期内的闭区间上的图象;(2)说明此函数图象可由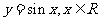 上的图象经怎样的变换得到;(3)求使f(x)<0时x的取值范围。
上的图象经怎样的变换得到;(3)求使f(x)<0时x的取值范围。
21(本小题满分13分)
已知函数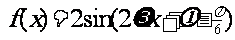 ,
,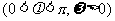 为偶函数,且函数
为偶函数,且函数
y=f(x)图象的两相邻对称轴间的距离为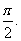 (1)求f(
(1)求f(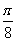 )的值;
)的值;
(2)将函数y=f(x)的图象向右平移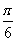 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
18. 19.
17.(本小题满分12分)
已知函数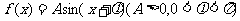 ,
,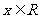 的最大值是1, 其图象经过点
的最大值是1, 其图象经过点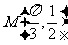 . (1)求
. (1)求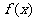 的解析式;(2)求
的解析式;(2)求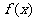 的单调区间。
的单调区间。
16.(本小题满分12分)
(1)若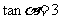 ,求
,求
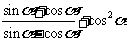 之值;
之值;
(2)化简: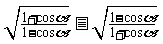 ,其中
,其中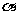 为第二象限角。
为第二象限角。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com