锐角三角函数

从近年广东省中考数学试题来看，解直角三角形的应用是中考的重点考查内容之一。

考点1：锐角三角函数的定义

8、10年第8题：如图,已知Rt△ABC中,斜边BC上的高AD＝4,cosB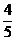＝,则AC＝　　　 .

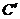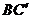21、12年第21题： 如图，在矩形纸片ABCD中，AB = 6，BC = 8。把△BCD沿对角线BD折叠，使点C落在处， 交AD于点G；E、F分别是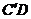和BD上的点，线段EF交AD于点H，把△FDE沿EF折叠，使点D落在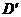处，点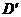恰好与点A重合。

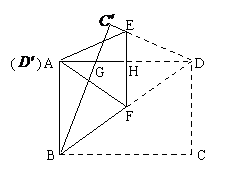（1）求证：△ABG≌△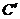DG；（2）求tan∠ABG的值；（3）求EF的长。

21、11年第21题：（相似三角形、函数、等腰三角形）

如图（1），△ABC与△EFD为等腰直角三角形，AC与DE重合，AB=AC=EF=9，∠BAC=∠DEF=90º，固定△ABC，将△DEF绕点A顺时针旋转，当DF边与AB边重合时，旋转中止．现不考虑旋转开始和结束时重合的情况，设DE，DF(或它们的延长线)分别交BC(或它的延长线) 于G，H点，如图(2)

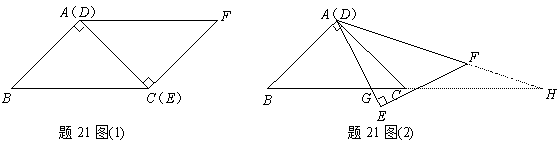
（1）问：始终与△AGC相似的三角形有　　 及　　 ；

（2）设CG=x，BH=y，求y关于x的函数关系式（只要求根据图(2)的情形说明理由）

（3）问：当x为何值时，△AGH是等腰三角形.

20、10年第20题：已知两个全等的直角三角形纸片ABC、DEF，如图（1）放置，点B、D重合，点F在BC上，AB与EF交于点G.∠C＝∠EFB＝90°，∠E＝∠ABC＝30°，AB＝DE＝4．

（1）求证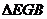：是等腰三角形；

（2）若纸片DEF不动，问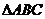绕点F逆时针旋转最小____度时，四边形ACDE成为以ED为底的梯形（如图（2））．求此梯形的高．

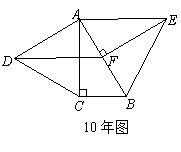
20、09年第20题：（1）如图1，圆内接△ABC中，AB=BC=CA，OD、OE为⊙O的半径，OD⊥BC于点F，OE⊥AC于点G，求证：阴影部分四边形OFCG的面积是△ABC的面积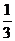的.

（2）如图2，若∠DOE保持120°角度不变，求证：当∠DOE绕着O点旋转时，由两条半径和△ABC的两条边围成的图形（图中阴影部分）面积始终是△ABC的面积的.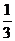

21、08年第21题：

（1）如图7，点O是线段AD的中点，分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD，连结AC和BD，相交于点E，连结BC．

求∠AEB的大小；

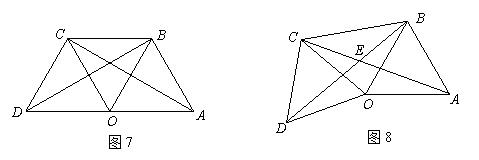（2）如图8，ΔOAB固定不动，保持ΔOCD的形状和大小不变，将ΔOCD绕着点O旋转（ΔOAB和ΔOCD不能重叠)，求∠AEB的大小.

19、11年第19题：如图，直角梯形纸片ABCD中，AD//BC，∠A=90º，∠C=30º．折叠纸片使BC经过点D，点C落在点E处，BF是折痕，且BF=CF=8．

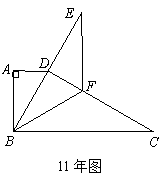（1）求∠BDF的度数；（2）求AB的长．

考点4：压轴题：图形的变换（旋转）证明

18、10年第18题：如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE。已知∠BAC=30º，EF⊥AB，垂足为F，连结DF。

（1）试说明AC=EF；　　 （2）求证：四边形ADFE是平行四边形。

18、13年第18题：

如图8，四边形ABCD是菱形，对角线AC与BD相交于O,AB=5,AO=4,求BD的长.

考点3：三角形与四边形的综合

18、09年第18题： 在菱形ABCD中，对角线AC与BD相交于点O，ＡＢ＝５，ＡＣ＝６.过Ｄ点作DE∥AC交ＢＣ的延长线于点Ｅ.

（１）求△BDE的周长；

（２）点Ｐ为线段BC上的点，

连接PO并延长交AD于点Q.求证：BP=DQ.

15、12年第15题：已知：如图，在四边形ABCD中，AB∥CD，对角线AC、BD相交于点O，BO = DO．求证：四边形ABCD是平行四边形．