
8.设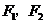 分别为双曲线
分别为双曲线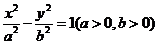 的左、右焦点,双曲线上存在一点
的左、右焦点,双曲线上存在一点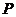 使得
使得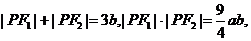 则该双曲线的离心率为( )
则该双曲线的离心率为( )
A.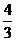 B.
B.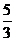 C.
C.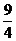 D.3
D.3
7.某几何体的三视图如图所示,则该几何体的表面积为( )
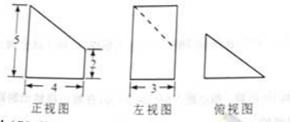
A.54 B.60 C.66 D.72
6.已知命题
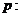 对任意
对任意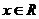 ,总有
,总有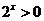 ;
;
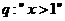 是
是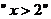 的充分不必要条件
的充分不必要条件
则下列命题为真命题的是( )
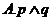
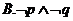
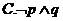
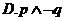
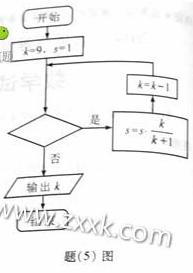
5.执行如题(5)图所示的程序框图,若输出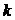 的值为6,则判断框内可填入的条件是( )
的值为6,则判断框内可填入的条件是( )
A.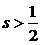 B.
B.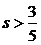 C.
C.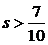 D.
D.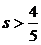
4.已知向量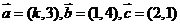 ,且
,且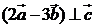 ,则实数
,则实数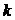 =( )
=( )
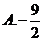
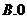
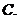
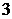 D.
D.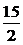
3.已知变量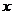 与
与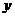 正相关,且由观测数据算得样本平均数
正相关,且由观测数据算得样本平均数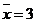 ,
,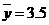 ,则由观测的数据得线性回归方程可能为( )
,则由观测的数据得线性回归方程可能为( )
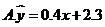
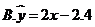
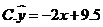
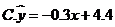
2.对任意等比数列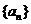 ,下列说法一定正确的是( )
,下列说法一定正确的是( )
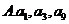 成等比数列
成等比数列
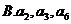 成等比数列
成等比数列
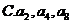 成等比数列
成等比数列
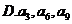 成等比数列
成等比数列
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在复平面内表示复数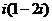 的点位于( )
的点位于( )
 第一象限
第一象限  第二象限
第二象限
 第三象限
第三象限 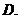 第四象限
第四象限
11.(本小题满分16分)已知直线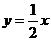 和
和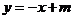 ,二次函数
,二次函数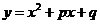
 图象的顶点为
图象的顶点为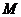
(1)若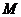 恰在直线
恰在直线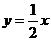 和
和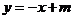 的交点处,证明无论m取何实数值,二次函数
的交点处,证明无论m取何实数值,二次函数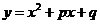 的图象与直线
的图象与直线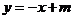 总有两个不同的交点;
总有两个不同的交点;
(2)在(1)的条件下,直线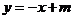 过点
过点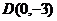 ,
, 二次函数
二次函数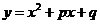 的图象与
的图象与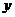 轴交于点C,与
轴交于点C,与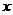 轴的左交点为
轴的左交点为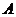 ,在直线
,在直线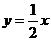 上求异于
上求异于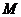 的点
的点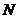 ,使
,使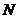 在
在 的外接圆
的外接圆 上.
上.
10.(本小题满分14分)两个男孩曹俊和伍岳在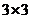 棋盘上用黑棋子和白棋子对局,规则如下:
棋盘上用黑棋子和白棋子对局,规则如下:
(I)他们轮流下子;(II)每轮到一次,就把一个棋子放在棋盘的空格里;(III)棋手轮到时,可选择一白子或一黑子,并且不必要总用同色;(IV)当棋盘填满时,某一行、列或对角线有偶数个黑棋子,曹俊就得1分,而某一行、列或对角线有奇数个黑棋子,伍岳就得1分;(V)棋手至少得到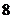 分中的
分中的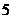 分,就算得胜.
分,就算得胜.
(1) 和局是否可能?若可能,请列出一种表格的情况;若不可能,请说明理由;
和局是否可能?若可能,请列出一种表格的情况;若不可能,请说明理由;
(2)叙述先下手的男孩的取胜策略.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com