
22. (本小题满分13分)
已知常数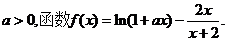
(I)
讨论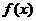 在区间
在区间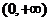 上的单调性;
上的单调性;
(II)
若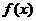 存在两个极值点
存在两个极值点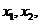 且
且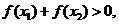 求
求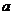 的zxxk取值范围.
的zxxk取值范围.
2014年普通高等学校招生全国统一考试(湖南卷)
数学(理工农医类)答案
21. (本小题满分13分)
如图7, 为坐标原点,椭圆
为坐标原点,椭圆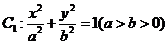 的左、右焦点分别为
的左、右焦点分别为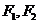 ,离心率为
,离心率为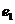 ;双曲线
;双曲线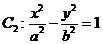 的左、右焦点分别为
的左、右焦点分别为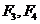 ,离心率为
,离心率为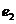 .已知
.已知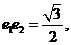 且
且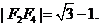
(I)
求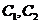 的方程;
的方程;
(II)
过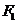 作
作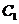 的不垂直于
的不垂直于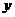 轴的弦
轴的弦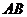 的中点.当直线
的中点.当直线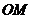 与
与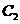 交于
交于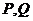 两点时,求四边形
两点时,求四边形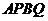 面积的最小值.
面积的最小值.
20. (本小题满分13分)
已知数列{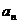 }满足
}满足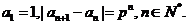
(I)
若{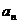 }是递增数列,且
}是递增数列,且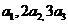 成等差数列,求
成等差数列,求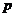 的值;
的值;
(II)
若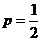 ,且{
,且{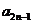 }是递增数列,{
}是递增数列,{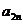 }是递减数列,zxxk求数列{
}是递减数列,zxxk求数列{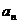 }的通项公式.
}的通项公式.
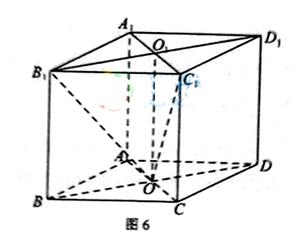
19. (本小题满分12分)
如图6,四棱柱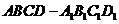 的所有棱长都相等,
的所有棱长都相等,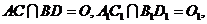 四边形
四边形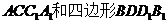 均为矩形.
均为矩形.
(I)
证明:
(II)
若 的余弦值.
的余弦值.
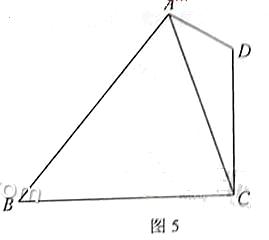
18. (本小题满分12分)
如图5,在平面四边形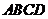 中,
中,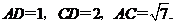
(I)
求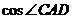 的值;
的值;
(II)
若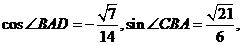 求zxxk
求zxxk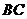 的长.
的长.
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别为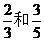 .现安排甲组研发新产品
.现安排甲组研发新产品 ,乙组研发新产品
,乙组研发新产品 .设甲、乙两组的研发相互独立.
.设甲、乙两组的研发相互独立.
(I) 求至少有一种新产品研发成功的概率;
(II)
若新产品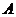 研发成功,预计企业可获利润120万元;若新产品
研发成功,预计企业可获利润120万元;若新产品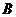 研发成功,预计企业可获利润100万元.求该企业可获利润的分布列和数学期望.
研发成功,预计企业可获利润100万元.求该企业可获利润的分布列和数学期望.
(二)必做题(14-16题)
14.若变量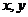 满足约束条件
满足约束条件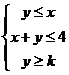 ,且
,且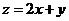 的最小值为-6,则
的最小值为-6,则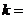
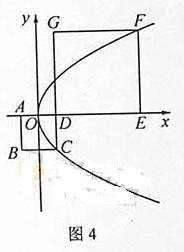
15.如图4,正方形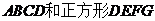 的边长分别为
的边长分别为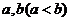 ,原点
,原点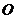 为
为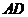 的中点,抛物线
的中点,抛物线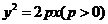 经过
经过
16.在平面直角坐标系中,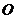 为原点,
为原点,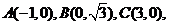 动点
动点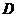 满足
满足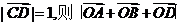 的最大值是
的最大值是
二、填空题:本大题共6小题,考生作答5小题,每小题5分,共25分.
(一)选做题(请考生在第11,12,13三题中任选两题作答,如果全做,则按前两题记分)
11.在平面直角坐标系中,倾斜角为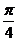 的直线
的直线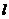 与曲线
与曲线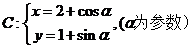 交于
交于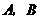 两点,则
两点,则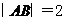 ,以坐标原点
,以坐标原点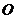 为极点,
为极点,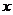 轴正半轴为极轴建立极坐标系,则直线
轴正半轴为极轴建立极坐标系,则直线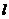 的极坐标方程是
的极坐标方程是
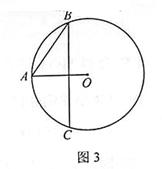
12.如图3,已知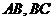 是
是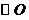 的两条弦,
的两条弦,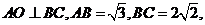 则
则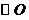 的半径等于
的半径等于
13.若关于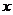 的不等式
的不等式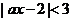 的解集为
的解集为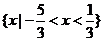 ,则
,则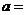
10.已知函数zxxk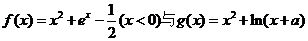 的图象上存在关于
的图象上存在关于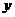 轴对称的点,则
轴对称的点,则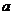 的取值范围是
的取值范围是
A.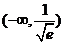 B.
B.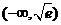 C.
C.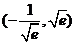 D.
D.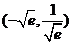
9.已知函数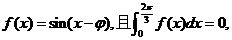 则函数
则函数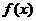 的图象的一条对称轴是
的图象的一条对称轴是
A.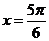 B.
B.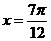 C.
C.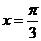 D.
D.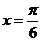
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com