
8.设甲、乙两个圆柱的底面积分别为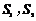 ,体积分别为
,体积分别为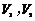 ,若它们的侧面积相等,且
,若它们的侧面积相等,且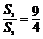 ,则
,则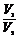 的值是
.
的值是
.
[答案]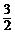
7.在各项均为正数的等比数列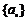 中,若
中,若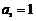 ,
,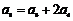 ,
,
则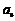 的值是
.
的值是
.
[答案]4
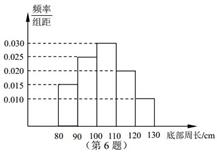
6.设抽测的树木的底部周长均在区间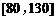 上,其频率分布
上,其频率分布
直方图如图所示,则在抽测的60株树木中,有 株
树木的底部周长小于100 cm.
[答案]24
5.已知函数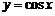 与
与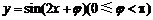 ,它们的图象有一个横坐标为
,它们的图象有一个横坐标为
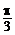 的交点,则
的交点,则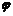 的值是
.
的值是
.
[答案]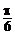
4.从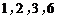 这4个数中一次随机地取2个数,则所取2个数的乘积为6的
这4个数中一次随机地取2个数,则所取2个数的乘积为6的
概率是 .
[答案]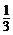
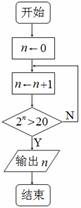
3.右图是一个算法流程图,则输出的n的值是 .
[答案]5
2.已知复数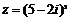 (i为虚数单位),则z的实部为
.
(i为虚数单位),则z的实部为
.
[答案]21
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1. 已知集合
已知集合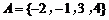 ,
,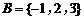 ,则
,则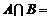 .
.
[答案]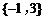
23.[必做题]本题主要考查简单的复合函数的导数,考查探究能力及运用数学归纳法的推理论证能力.满分10分.
(1)解:由已知,得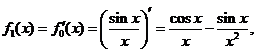
于是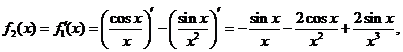
所以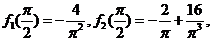
故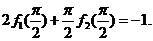
(2)证明:由已知,得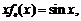 等式两边分别对x求导,得
等式两边分别对x求导,得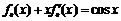 ,
,
即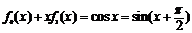 ,类似可得
,类似可得
 ,
,
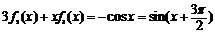 ,
,
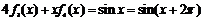 .
.
下面用数学归纳法证明等式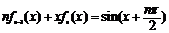 对所有的
对所有的 都成立.
都成立.
(i)当n=1时,由上可知等式成立.
(ii)假设当n=k时等式成立, 即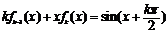 .
.
因为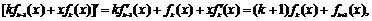
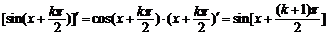 ,
,
所以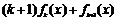
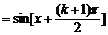 .
.
所以当n=k+1时,等式也成立.
综合(i),(ii)可知等式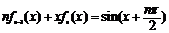 对所有的
对所有的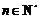 都成立.
都成立.
令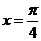 ,可得
,可得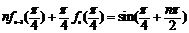 (
(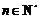 ).
).
所以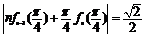 (
(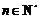 ).
).
23.(本小题满分10分)
已知函数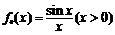 ,记
,记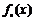 为
为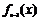 的导数,
的导数,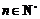 .
.
(1)求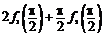 的值;
的值;
(2)证明:对任意的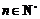 ,等式
,等式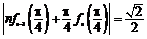 成立.
成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com