
7.下列函数中,满足“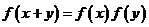 ”的单调递增函数是 ( )
”的单调递增函数是 ( )
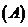
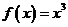
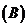
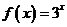
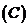
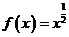
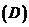
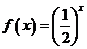
6.从正方形四个顶点及其中心这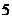 个点中任取
个点中任取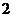 个点,则这
个点,则这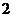 个点的距离小于正方形的边长的概率为
( )
个点的距离小于正方形的边长的概率为
( )
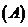
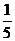
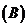
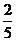
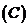
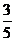
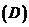

5.将边长为 的正方形以其一边所在直
的正方形以其一边所在直
线旋转轴旋转一周,所得几何体的侧面
积是 ( )
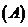

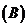
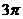
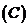
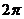
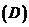

4.根据右边框图,对大于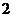 的正整数
的正整数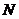 ,
,
输出的数列的通项公式是 ( )
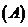
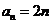
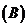
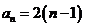
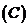
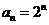
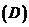
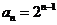
3.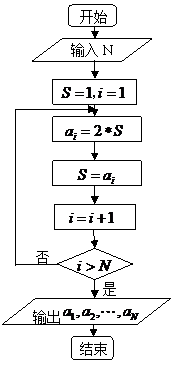 已知复数
已知复数 ,则
,则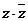 的值为
( )
的值为
( )
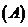
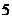
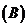
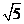
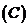
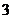
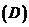

2.函数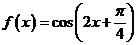 的最小正周期是
(
)
的最小正周期是
(
)
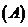
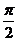
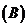

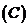
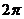
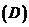

一、在每小题给出的四个选项中,只有一项符合要求.
1.设集合
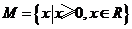 ,
,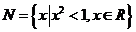 ,则
,则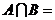 ( )
( )
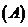
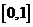
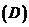
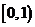
21.(本小题满分14分)
设函数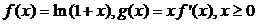 ,其中
,其中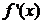 是
是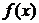 的导函数.
的导函数.
(Ⅰ)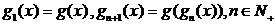 ,求
,求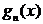 的表达式;
的表达式;
(Ⅱ)若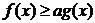 恒成立,求实数
恒成立,求实数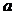 的取值范围;
的取值范围;
(Ⅲ)设 ,比较
,比较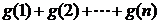 与
与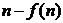 的大小,并加以证明.
的大小,并加以证明.
解:(Ⅰ)∵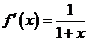 ,∴
,∴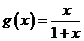 ,
,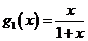 ,
,
∴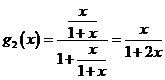 ,
,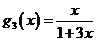 ,……,所以
,……,所以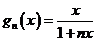 ;
;
用数学归纳法证明如下:
(1) 时结论成立;
时结论成立;
(2)假设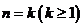 时结论成立,即
时结论成立,即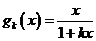 ,那么
,那么
当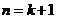 时,
时,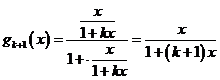 ,
,
即当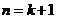 时结论也成立,
时结论也成立,
因此对任意的 ,
,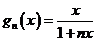 成立.
成立.
(Ⅱ)∵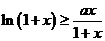 在
在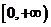 内恒成立,
内恒成立,
设 ,则
,则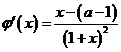 ,
,
若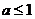 ,则
,则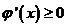 恒成立,所以
恒成立,所以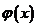 在
在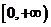 内单调递增,
内单调递增,
∴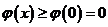 ;
;
若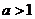 ,则在
,则在 内,
内,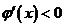 ,
,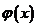 单调递减,可见
单调递减,可见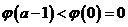 ,说明在
,说明在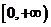 内,存在
内,存在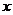 ,使
,使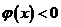 ,即
,即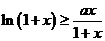 不恒成立,
不恒成立,
所以使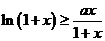 在
在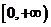 内恒成立的
内恒成立的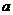 取值范围是
取值范围是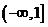 .
.
(Ⅲ)由题设知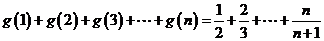 ,
,
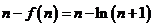 ,
,
猜想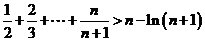 ,
,
证明:∵上式左边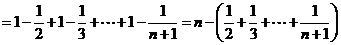 ,
,
∴上式等价于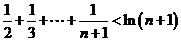 ,
,
在(Ⅱ)中,当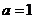 时,
时,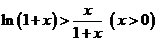 ,
,
令 ,则
,则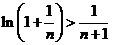 ,即
,即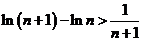 ,
,
所以 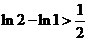
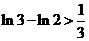
……
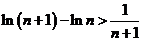 ,
,
叠加得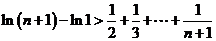 ,
,
即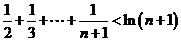 .
.
20.(本小题满分13分)
如图,曲线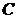 由上半椭圆
由上半椭圆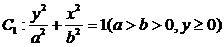 和部分抛物线
和部分抛物线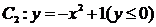 连接而成,
连接而成,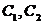 的公共点为
的公共点为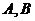 ,其中
,其中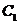 的离心率为
的离心率为 .
.
(Ⅰ)求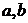 的值;
的值;
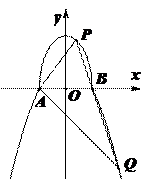 (Ⅱ)过点
(Ⅱ)过点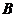 的直线
的直线 与
与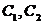 分别交于
分别交于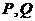 (均异于点
(均异于点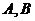 ),若
),若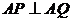 ,求直线
,求直线 的方程.
的方程.
解:(Ⅰ)以题意知,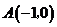 ,
,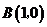 ,
,
∴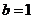 ,又
,又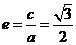 ,解得
,解得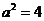 ,
,
∴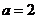 ,
,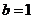 .
.
(Ⅱ)设直线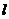 的方程是
的方程是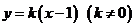 ,
,
由方程组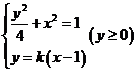 ,得
,得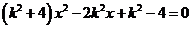 ,
,
设 ,则
,则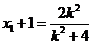 ,
,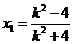 ,
,
∴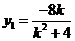 ,
,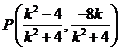 ,
, ,∵
,∵ ,∴
,∴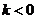 ;
;
由方程组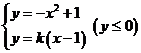 ,得
,得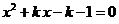 ,
,
设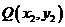 ,则
,则 ,∴
,∴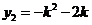 ,
,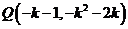 ,
,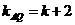 ,
,
∵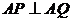 ,∴
,∴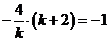 ,解得
,解得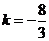 ,经检验符合题意,
,经检验符合题意,
所以直线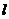 的方程是
的方程是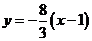 .
.
19.(本小题满分12分)
在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上
的产量具有随机性,且互不影响,其具体情况如下表:
|
作物产量(kg) |
300 |
500 |
|
概 率 |
0.5 |
0.5 |
|
作物市场价格(元/kg) |
6 |
10 |
|
概 率 |
0.4 |
0.6 |
(Ⅰ)设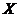 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求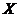 的分布列;
的分布列;
(Ⅱ)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元
的概率.
解:(Ⅰ)以题意,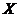 的值可为:
的值可为: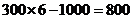 ;
;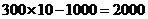 ;
; ;
;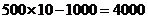 ,
,
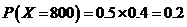 ,
,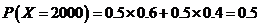 ,
,
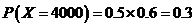 ,
,
所以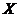 的分布列为
的分布列为
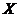 |
800 |
2000 |
4000 |
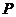 |
0.2 |
0.5 |
0.3 |
(Ⅱ)设这3季中至少有2季的利润不少于2000元为事件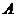 ,则
,则
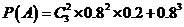
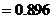 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com