
5. 已知二次函数f(x)的图象是一条开口向下的抛物线,且对任意x∈R,均有f(1-x)=f(1+x) 成立。下列不等式中正确的是( )
(A) 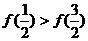 (B) f(-1)>f(2)
(B) f(-1)>f(2)
(C) f(-1)<f(2) (D) f(0)<0
4.某工厂有甲、乙、丙、丁四类产品的数量成等比数列,共计3000件,现要用 分层抽样的方法从中抽取150件进行质量检测,其中乙
分层抽样的方法从中抽取150件进行质量检测,其中乙 、丁两类产品抽取的总数为100件,则甲类产品共有( )
、丁两类产品抽取的总数为100件,则甲类产品共有( )
A.1 00件 B.200件 C.300件
00件 B.200件 C.300件  D.400件
D.400件
3. 双曲线 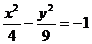 的焦点的坐标是( )
的焦点的坐标是( )
(A) ( ±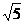 ,0)
(B) (±
,0)
(B) (±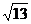 ,0)
,0)
(C) ( 0,±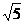 )
(D) (0,±
)
(D) (0,±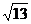 )
)
2.复数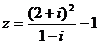 (
(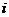 是虚数单位)在复平面上对应的点位于 (
是虚数单位)在复平面上对应的点位于 (  )
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
一、选择题
1. 设M、N是两个非空集合,且M={a|a∈N},则M、N 间的关系为( )
(A) M=N (B) M是N的真子集
(C) M是N的子集  (D) M∈N
(D) M∈N
22、解:(1)设双曲线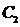 的方程为
的方程为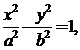 则
则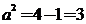
再由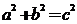 得
得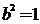 ,故
,故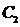 的方程为
的方程为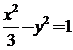 ………………..(5分)
………………..(5分)
(2)将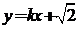 代入得
代入得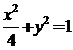 ,得
,得
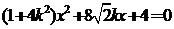 ,…………………………………………….(7
,…………………………………………….(7 分)
分)
由直线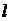 与
与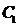 恒有两个不同的交点
恒有两个不同的交点 ,得:
,得:
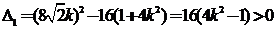 ,即
,即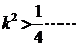 ①………(8分)
①………(8分)
将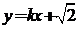 代入
代入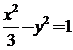 ,得
,得
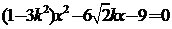 ,由直线
,由直线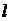 与
与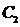 恒有两个不同的交点,得:
恒有两个不同的交点,得:
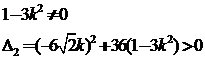
即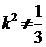 且
且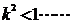 ②……………………………………………(9分)
②……………………………………………(9分)
设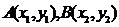 ,则
,则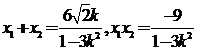 (10分)
(10分)
由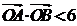 得
得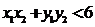 ,而
,而

21、解:(1)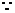 点
点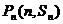 都在函数
都在函数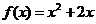 的图象上,
的图象上,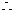
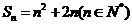 ,当
,当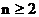 时,
时,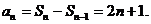 当n=1时,
当n=1时,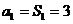 满足上式,所以数列
满足上式,所以数列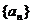 的通项公式为
的通项公式为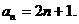 (4分)
(2)由
(4分)
(2)由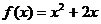 求导得
求导得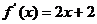 .
. 过点
过点 的切线的斜率为
的切线的斜率为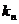 ,
,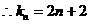 .
.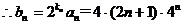 .
.
 设等差数列的公差为
设等差数列的公差为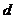 ,则
,则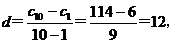
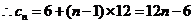 ,即为
,即为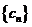 的通项公式. (14分)
的通项公式. (14分)
20、解:(1)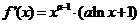 ,易知
,易知
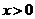 ,
,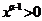 .
当
.
当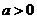 时,令
时,令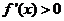 得
得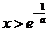 ,所以
,所以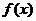 的单增区间为
的单增区间为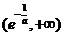 ,
同
,
同 理,单减区间为
理,单减区间为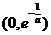 ;
当
;
当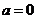 时,
时,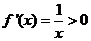 ,所以
,所以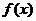 在
在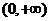 上单增;
当
上单增;
当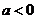 时,令
时,令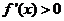 得
得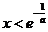 ,所以
,所以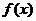 的单增区间为
的单增区间为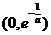 ,
同理,单减区间为
,
同理,单减区间为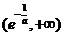 . (8分)
(2)当
. (8分)
(2)当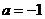 时,
时,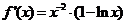 .令
.令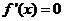 得
得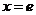 .列表如下:
.列表如下:
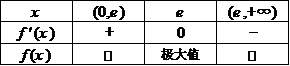 所以,
所以,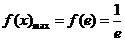 . (12分)
. (12分)
19、 证:(1)记AC与BD的交点为O,连接EO,则可证BF∥EO,又
证:(1)记AC与BD的交点为O,连接EO,则可证BF∥EO,又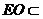 面ACE,
面ACE,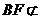 面ACE,故BF∥平面ACE; (3分)
面ACE,故BF∥平面ACE; (3分)
 解
解 :(2)
:(2)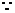 ABCD为正方形,
ABCD为正方形,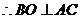 ,
,
 的大小为
的大小为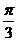 ; (8分)
; (8分)

|
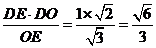 . (12分)
(本题运用向量法解答正确,请参照给分)
. (12分)
(本题运用向量法解答正确,请参照给分)17、 解:(I)
解:(I)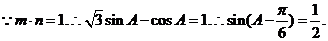 ………2分
………2分
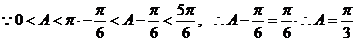 …………6分
…………6分
(Ⅱ)由题知
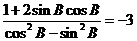
 ,整理得
,整理得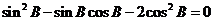 …8分
…8分
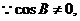

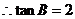 或
或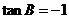 。………10 分
。………10 分
而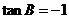 使
使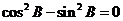 ,舍去
,舍去
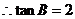 ……………………………………………………………………12
分
……………………………………………………………………12
分
另解: 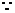
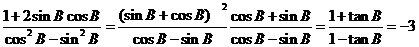
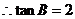
 所以
所以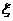 的分布列为
的分布列为
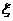 |
0 |
1 |
2 |
3 |
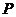 |
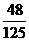 |
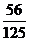 |
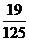 |
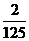 |
所以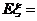 0×
0×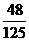 +1×
+1×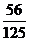 +2×
+2×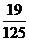 +3
+3 ×
×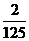 =
=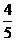 .…………………………12分
.…………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com