
22(本小题满分12分).已知圆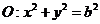 与直线
与直线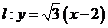 相切。
相切。
(1)求以圆O与y轴的交点为顶点,直线在x轴上的截距为半长轴长的椭圆C方程;
(2)已知点A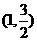 ,若直线与椭圆C有两个不同的交点E,F,且直线AE的斜率与直线AF的斜率互为相反数;问直线的斜率是否为定值?若是求出这个定值;若不是,请说明理由.
,若直线与椭圆C有两个不同的交点E,F,且直线AE的斜率与直线AF的斜率互为相反数;问直线的斜率是否为定值?若是求出这个定值;若不是,请说明理由.
安师大附中2012届高三第三次模拟考试
21.(满分12分)设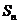 为数列
为数列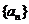 的前
的前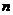 项和,对任意的
项和,对任意的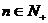 ,都有
,都有
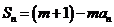
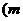 为常数,且
为常数,且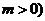 .
.
(1)求证:数列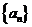 是等比数列;
是等比数列;
(2)设数列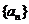 的公比
的公比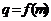 ,数列
,数列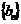 满足
满足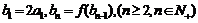 ,求数列
,求数列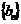 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列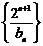 的前
的前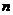 项和
项和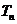 .
.
20. (本小题满分12分)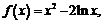

(1)求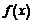 的最小值;(2)若
的最小值;(2)若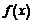 ≥
≥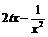 在
在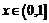 内恒成立,求
内恒成立,求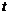 的取值范围
的取值范围
19.(本小题满分12分)如图,已知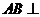 平面
平面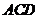 ,
,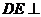 平面
平面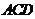 ,△
,△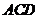 为等边三角形,
为等边三角形,
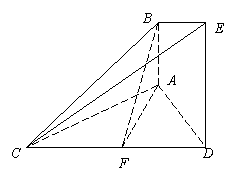
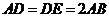 ,
,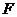 为
为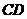 的中点.
的中点.
(1) 求证: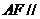 平面
平面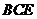 ;
;
(2) 求证 :平面
:平面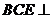 平面
平面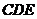 ;
;
(3) 求直线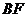 和平面
和平面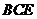 所成角的正弦值.
所成角的正弦值.
18. (本小题满分12分)定义在R上的奇函数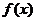 有最小正周期4,且
有最小正周期4,且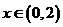 时,
时,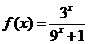 。
。
⑴求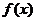 在
在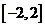 上的解析式;
上的解析式;
⑵判断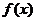 在
在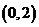 上的单调性,并给予证明;
上的单调性,并给予证明;
⑶当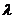 为何值时,关于方程
为何值时,关于方程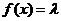 在
在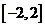 上有实数解?
上有实数解?
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)△ABC的角A、B、C的对边分别为a、b、c,=(2b-c,a),=(cosA,-cosC),且⊥. (Ⅰ)求角A的大小;
(Ⅱ)当y=2sin2B+sin(2B+)取最大值时,求角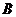 的大小.
的大小.
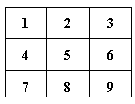
16.用红、黄、蓝三种颜色之一去涂图中标号为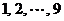 的
的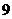 个小正方形(如下图),使得任意相邻(有公共边的)小正方形
个小正方形(如下图),使得任意相邻(有公共边的)小正方形
所涂颜色都不相同,且标号为“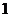 、
、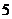 、
、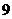 ”的小正方形涂相同的颜色,则符合条件的所有涂法共有 种
”的小正方形涂相同的颜色,则符合条件的所有涂法共有 种 .
.
15. 若直线
若直线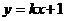 与圆
与圆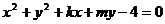 相交于P、Q两点,且点P、Q关于直线
相交于P、Q两点,且点P、Q关于直线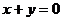 对称,则不等式组
对称,则不等式组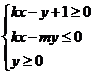 表示的平面区域的面积为________.
表示的平面区域的面积为________.
14. 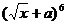 的展开式中x2项的系数为60,则实数a=
的展开式中x2项的系数为60,则实数a=
二、填空题:本大题共5小题,每小题5分,共25分.
13.若不等式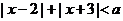 的解集为
的解集为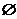 ,则
,则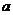 的取值范围为
.
的取值范围为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com