
37. 解(1)设金属线框刚进入磁场区域abcd的速度为v1,则线框中产生的感应电动势
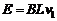 (1分)
(1分)
安培力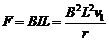 (1分)
(1分)
依题意,有: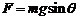 (1分)
(1分)
线框下滑距离s的过程中,根据机械能守恒定律,有:
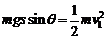 (2分)
(2分)
联立以上各式解得: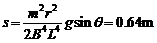 (2分)
(2分)
(2)设金属线框刚全部进入水平导轨时速度为v2,线框在倾斜轨道上运动的全过程中,根据动能定理,有:
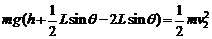 (2分)
(2分)
解得: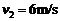 (1分)
(1分)
线框进入水平导轨的磁场中后由于受到安培力作用而减速直至速度减为零,线框在穿越任一磁场区域的过程中,根据动量定理,有:
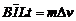 ,即
,即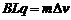 (2分)
(2分)
又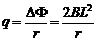 (1分)
(1分)
所以,线框在穿越每一磁场区域速度的减少量相同,且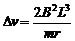 (1分)
(1分)
线框在水平导轨上穿越磁场区域的个数
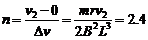 (1分)
(1分)
金属框能穿越导轨水平部分中2个完整的磁场区域. (1分)
(3)整个过程中,根据能量守恒定律,有:
金属线框内产生的焦耳热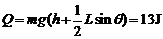 . (4分)
. (4分)
36.解:⑴达到最大速度时,金属框及物体的加速度为零,有:
Mg=T T=mgsin37°+F F=(B2-B1)IL=KIL2 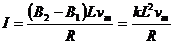
解以上方程,可解得: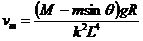
⑵设产生的焦耳热为Q,根据能量守恒定律,有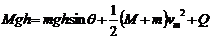
得: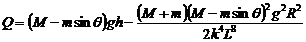
⑶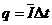
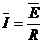
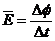
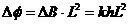 解得:
解得: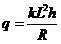
35. 解:(1) b穿越磁场过程中产生的总热量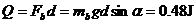 (2分)
(2分)
其中导体棒b上产生的焦耳热 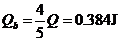 (2分)
(2分)
(2) 在a穿越磁场的过程中,导体棒a上通过的电量
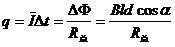 (2分)
(2分)
 解得
解得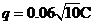 (1分)
(1分)
(3) 导体棒b匀速运动时有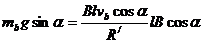 (1分)
(1分)
其中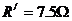 ,解得
,解得 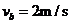 (1分)
(1分)
则导体棒a进入磁场时的速度 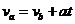
其中t为导体棒进入磁场瞬间运动的总时间且t=0.5s
解得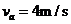 (1分)
(1分)
对导体棒a研究有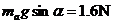 (1分)
(1分)
导体棒a受到的安培力 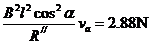 (其中
(其中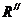 =5Ω)(1分)
=5Ω)(1分)
所以a进入磁场时做减速运动
由牛顿第二定律 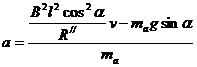 (1分)
(1分)
所 以
以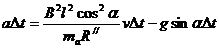 (1分)
(1分)
有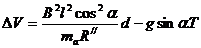 ,解得
,解得 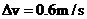 (1分)
(1分)
所以导体棒a离开磁场时的速度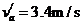 (1分)
(1分)
34.解:(1)根据左手定则判断知b棒向左运动。 (1分)
a棒从h0高 处释放后在弯曲导轨上滑动时机械能守恒,有
处释放后在弯曲导轨上滑动时机械能守恒,有
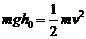
得 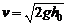 (1分)
(1分)
a棒刚进入磁场I时 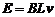
此时感应电流大小 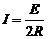
此时b棒受到的安培力大小 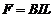
依题意,有 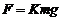 (1分)
(1分)
求得 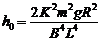 (1分)
(1分)
(2)由于a棒从小于进入h0释放,因此b棒在两棒相碰前将保持静止。
流过电阻R的电量 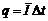
又 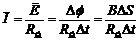 (1分)
(1分)
所以在a棒穿过磁场I的过程中,通过电阻R的电量
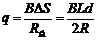 (1分)
(1分)
将要相碰时a棒的速度
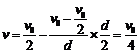 (1分)
(1分)
此时电流 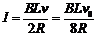 (1分)
(1分)
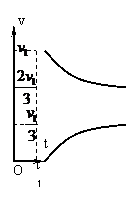 此时b棒电功率
此时b棒电功率 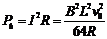 (1分)
(1分)
(3)由于a棒从高度大于h0处释放,因此当a棒进入磁场I后,b棒开始向左运动。由于每时每刻流过两棒的电流强度大小相等,两磁场的磁感强度大小也相等,所以两棒在各自磁场中都做变加速运动,且每时每刻两棒的加速度大小均相同,所以当a棒在t1时间内速度改变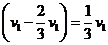 时,b棒速度大小也相应改变了
时,b棒速度大小也相应改变了
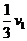 ,即此时b棒速度大小为
,即此时b棒速度大小为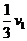 。 (1分)
。 (1分)
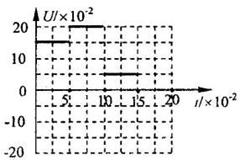
两棒的速度大小随时间的变化图像大致如右图所示: (2分)
通过图像分析可知,在t1时间内,两棒运动距离之和为v1t1,所以在t1时间内b棒向左运动的距离为ΔS=(v1t1-d),
距离磁场II左边界距离为
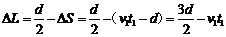 。 (2分)
。 (2分)
33. 解:(1)磁场的磁感应强度在时间t内由B均匀减小到零,说明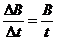
此过程中的感应电动势为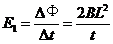 ①
①
通过R的电流为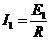 ②
②
此过程中电阻R上产生的焦耳热为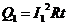 ③, 联立①②③求得
③, 联立①②③求得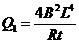
(2)①ab杆离起始位置的位移从L到3L的过程中.由动能定理可得
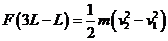 ④
④
ab杆刚要离开磁场时,感应电动势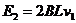 ⑤
⑤
通过R的电流为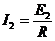 ⑥
⑥
水平方向上受安培力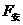 和恒力F作用
和恒力F作用
安培力为: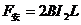 ⑦ 联立⑤⑥⑦解得
⑦ 联立⑤⑥⑦解得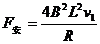 ⑧
⑧
由牛顿第二定律可得: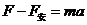 ⑨
⑨
联立④⑧⑨解得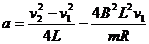
②ab杆在磁场中由起始位置发生位移L的过程中,根据功能关系,恒力F做的功等于ab杆增加的动能与回路产生的焦耳热之和,则
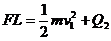 ⑩
⑩
联立④⑩解得 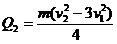
32. 解:(1)(10分)导体棒ab刚开始运动时的速度为零,由欧姆定律
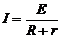 (1分)
(1分)
导体棒ab受安培力 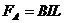 (1分)
(1分)
牛顿第二定律
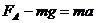 (1分)
(1分)
导体棒ab开始运动时的加速度 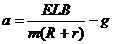 (1分)
(1分)
设导体棒ab向上运动的最大速度为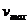 ,当导体棒所受重力与安培力相等时,达到最大速度,回路电流为
,当导体棒所受重力与安培力相等时,达到最大速度,回路电流为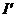
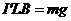 (2分)
(2分)
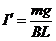
由欧姆定律 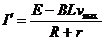 (2分)
(2分)
得 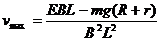 (2分)
(2分)
(2)(4分)电源的输出功率 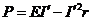 (2分)
(2分)
P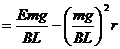 (2分)
(2分)
(3)(6分)电源的电能转化为导体棒的机械能和电路中产生的焦耳热之和(1分)
△t时间内:电源的电能 △E电 = 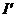 E △t
E △t 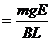 △t
(1分)
△t
(1分)
导体棒ab增加的机械能
△E机= mg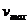 △t = mg
△t = mg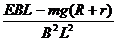 △t (1分)
△t (1分)
电路中产生的焦耳热 Q=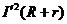 △t=
△t=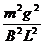 (R+r)△t (1分)
(R+r)△t (1分)
△t时间内,导体棒ab增加的机械能与电路中产生的焦耳热之和为△E’
△E’= △E机 + Q (1分)
△E’= mg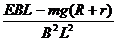 △t +
△t + 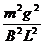 (R+r)△t
(R+r)△t
整理得 △E’ 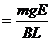 △t
(1分)
△t
(1分)
由此得到 △E电 =△ E’,回路中能量守恒。
31. 解:(1)金属杆在恒定外力F作用下,沿下层导轨以加速度a做匀加速直线运动,根据运动学公式有vP2=2as……………………………………………………………………………1分
将vP=4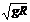 ,s=4R代入,可解得a=2g…………………………………………………1分
,s=4R代入,可解得a=2g…………………………………………………1分
根据牛顿第二定律,金属杆沿下层导轨运动时,在竖直方向和水平方向分别有
mg-N-Fsinθ=0,Fcosθ-μN=ma………………………………………………………2分
解得 F=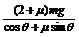 ……………………………………………………………………1分
……………………………………………………………………1分
(2)设金属杆从PP′位置运动到轨道最高位置MM′时的速度为v1,
此过程根据机械能守恒定律有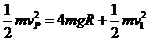 ………………………………2分
………………………………2分
解得 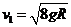 …………………………………………………………………………1分
…………………………………………………………………………1分
设金属杆在MM′位置所受轨道压力为FM,
根据牛顿第二定律有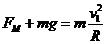 …………………………………………………2分
…………………………………………………2分
解得 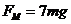 ………………………………………………………………………1分
………………………………………………………………………1分
由牛顿第三定律可知,金属杆对轨道压力的大小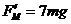 ………………………1分
………………………1分
(3)经历一段极短的时间Δt1,在安培力F1作用下杆的速度由v1减小到v2,接着在安培力F2作用下经历一段极短的时间Δt2,杆的速度由v2减小到v3,再接着在安培力F3作用下经历一段极短的时间Δt3,杆的速度由v3减小到v4,……再接着在安培力Fn作用下经历一段极短的时间Δtn,杆的速度由vn减小到vn+1。
由动量定理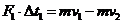 …………………………………………………………1分
…………………………………………………………1分
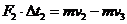
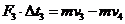
……
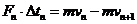 ……………………………………………………………………1分
……………………………………………………………………1分
在每一段极短的时间内,杆的速度、杆上的电动势和安培力都可认为是不变的,
则Δt1时间内,安培力 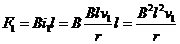 ………………………………1分
………………………………1分
则Δt2时间内,安培力 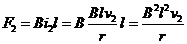
则Δt3时间内,安培力 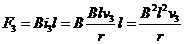 ………………………………1分
………………………………1分
……
冲量累加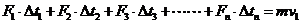 ………………………………1分
………………………………1分
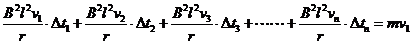
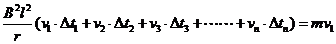 …………………………………1分
…………………………………1分
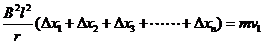
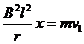 …………………………………………………………………………………1分
…………………………………………………………………………………1分
解得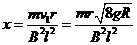 …………………………………………………………………1分
…………………………………………………………………1分
30.解:(1)线框匀速运动,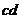 切歌磁感线
切歌磁感线
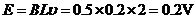 (2分)
(2分)
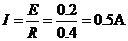 (2分)
(2分)
线框受安培力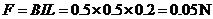 (2分)
(2分)
(2)产生热量有两个阶段: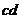 、
、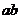 分别在两磁场边界间运动
分别在两磁场边界间运动
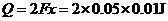 (3分)
(3分)
(3) 在两磁场边界件运动 运动时间
在两磁场边界件运动 运动时间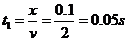 (1分)
(1分)
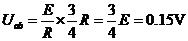 (2分)
(2分)
 在右磁场中运动同时
在右磁场中运动同时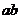 在左磁场中运动,
在左磁场中运动,
运动时间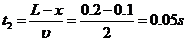 (1分)
(1分)
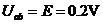 (2分)
(2分)
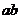 在两磁场边界间运动 运动时间
在两磁场边界间运动 运动时间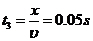 (1分)
(1分)
29. (1)设ab棒进入水平导轨的速度为v1,ab棒从圆弧导轨滑下机械能定恒:
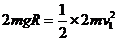 ① (2分)
① (2分)
离开导轨时,设ab棒的速度为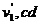 棒的速度为
棒的速度为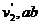 棒与
棒与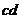 棒在水平导轨上运动,
棒在水平导轨上运动,
动量定恒,
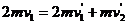 ② (2分)
② (2分)
依题意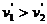 ,两棒离开导轨做平抛运动的时间相等,
,两棒离开导轨做平抛运动的时间相等,
由平热量运动水平位移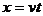 可知
可知
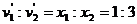 ③ (2分)
③ (2分)
联立①②③解得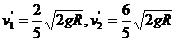 (2分)
(2分)
(6分)(2)ab棒刚进入水平导轨时,cd棒受到的安培力最大,此时它的加速度最大,设此时回路的感应电动势为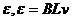 ④ (1分)
④ (1分)
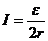 ⑤ (1分)
⑤ (1分)
cd棒受到的安培力为: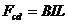 ⑥ (1分)
⑥ (1分)
根据牛顿第二定律,cd棒有最大加速度为
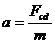 ⑦ (1分)
⑦ (1分)
联立④⑤⑥⑦解得:
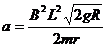 (2分)
(2分)
(4分)(3)根据能量定恒,两棒在轨道上运动过程产生的焦耳热为:
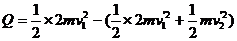 ⑧ (2分)
⑧ (2分)
联立①⑧并代入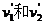 解得:
解得:
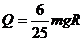
28. 解:(1)设某时刻ab的速度为v
则感应电动势E=BLv ① 电流强度 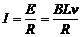 ②
②
棒所受安培力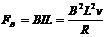 ③
③
则由牛顿第二定律得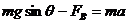 ④
④
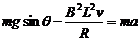 当a=0时,有
当a=0时,有 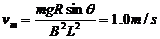 ⑤
⑤
(2)设t时刻棒的加速度为a,速度为v,产生的电动势为E(t+△t)(△t→0)时刻,棒的速度为(v+△v),电动势为E′
则E=BLv E′=BL(v+△v)
△t内流过棒截面的电荷量 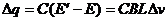 ⑥
⑥
电流强度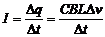 ⑦
⑦
棒受的安培力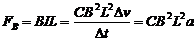 ⑧
⑧
由牛顿第二定律,t时刻对棒有 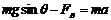 ⑨
⑨
即 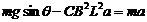
故 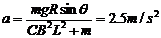 故棒做匀加速直线运动。
故棒做匀加速直线运动。
当t=4s时,V=at=10m/s 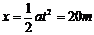
由能量守恒: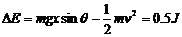
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com