27、(本题满分12分)

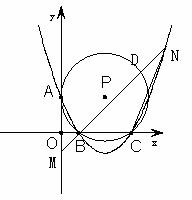
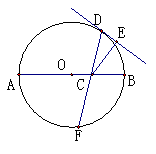
已知如图，抛物线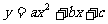与x轴相交于B(1，0)、C(4，0)两点，与y轴的正半轴相交于A点，过A、B、C三点的⊙P与y轴相切于点A．M为y轴负半轴上的一个动点，直线MB交⊙P于点D，交抛物线于点N。

⑴ 请求出点A坐标和⊙P的半径；

⑵ 请确定抛物线的解析式；

⑶若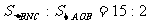，求N点坐标。

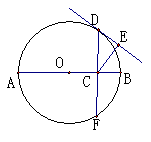
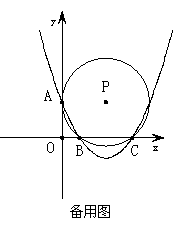(4)若△AOB与以A、B、D为顶点的三角形相似，求MB•MD的值．(先画出符合题意的示意图再求解)。

26、(本题满分12分)

图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合)。

(1)操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连结AD、BE，CE的延长线交AB于F(图2)；

探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论。

(2)操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移(当点P与点F重合时停止移动)，平移后的△CDE设为△PQR；

探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围.

(3)操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设∠AC C′=α(30°＜α＜90°(图4)；

探究：在图4中，线段C′N·E′M的值是否随α的变化而变化？如果没有变化，请你求出C′N·E′M的值，如果有变化，请你说明理由.

24、(本题满分8分)

已知：a、b、c是△ABC的∠A、∠B、∠C的对边，a＞b，关于x的方程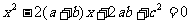有两相等的实数根，且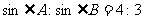，若△ABC外接圆面积为25π，求△ABC的周长.

23、(本题满分9分)

在平面直角坐标系中给定以下五个点A(－2，0)、B(1，0)、C(4，0)、D(－2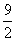，)、E(0，－6)，从这五个点中选取三点，使经过三点的抛物线满足以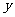轴的平行线为对称轴。我们约定经过A、B、E三点的抛物线表示为抛物线ABE。

(1)符合条件的抛物线共有多少条？不求解析式，请用约定的方法一一表示出来；

(2)在五个形状、颜色、质量完全相同的乒乓球上标上A、B、C、D、E代表以上五个点，玩摸球游戏，每次摸三个球。请问：摸一次，三球代表的点恰好能确定一条符合条件的抛物线的概率是多少？

(3)小强、小亮用上面的五球玩游戏，若符合要求的抛物线开口向上，小强可以得1分；若抛物线开口向下小亮得5分，你认为这个游戏谁获胜的可能性大一些？说说你的理由。

22、(本题满分8分)

已知：如图，从以AB为直径的圆上一点D引一切线，再从AB上一点C引这条切线的垂线，垂足为E。

(1)如果DC⊥AB且DC交圆于点F，请证明：CE·AB=AC·CB+CD²

(2)如果DC与AB不垂直，那(1)中结论是否还成立？请证明你的想法。

21、(本题满分6分)

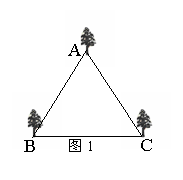
某公园有一个边长为4米的正三角形花坛，三角形的顶点A、B、C上各有一棵古树．现决定把原来的花坛扩建成一个圆形或平行四边形花坛，要求三棵古树不能移动，且三棵古树位于圆周上或平行四边形的顶点上．以下设计过程中画图工具不限．

(1)按圆形设计，利用图1画出你所设计的圆形花坛示意图；

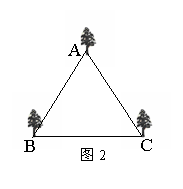
(2)按平行四边形设计，利用图2画出你所设计的平行四边形花坛示意图；

(3)若想新建的花坛面积较大，选择以上哪一种方案合适？请说明理由．

20、(本题满分6分)

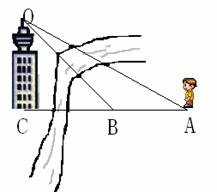
如图，要在河的一侧测量对岸水塔的高度，小明设计了如下的测量方案：先在河的这侧选取一点A，测得水塔顶点O的仰角为 30^o，再朝着水塔方向前进20米到达B处，这时测得与水塔顶点O的仰角为45^o，你能根据这些数据算出水塔高度吗？(结果可保留根号)

19、(本题满分8分)我国年人均用纸量约为28公斤，每个初中毕业生离校时大约有10公斤废纸；用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树，而平均每亩森林只有50至80棵这样的大树.

(1)　 若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使多少亩森林免遭砍伐.

(2)　 深圳市从2000年初开始实施天然林保护工程,大力倡导废纸回收再生，如今成效显著,森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩.假设我市年用纸量的20%可以作为废纸回收、森林面积年均增长率保持不变，请你按全市总人口约为1000万计算:在从2005年初到2006年初这一年度内，我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的百分之几.(精确到1%)

18．如图9，在ΔABC中，∠C=90°，AC=8，AB=10，点P在AC上，AP=2，若⊙O的圆心在线段BP上，且⊙O与AB、AC都相切，则⊙O的半径是　　　　 。