
7.从总体数为N的一批零件中抽取一个容量为30的样本,若每个零件被抽取的概率为0.25,则N为
A.130 B.200 C.120 D.100
6.设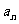 为二项式
为二项式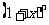 的展开式中
的展开式中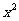 的系数,则
的系数,则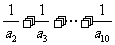 的值为
的值为
A.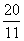 B.
B.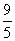 C.1 D.2
C.1 D.2
5.以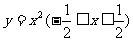 图象上一点P
为切点的切线
图象上一点P
为切点的切线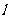 的倾斜角的取值范围是
的倾斜角的取值范围是
A.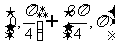 B.
B.
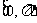 C.
C.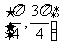 D.
D.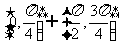
4.如图,正方体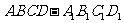 中,点P在线段
中,点P在线段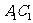 上运动,异面直线BP与
上运动,异面直线BP与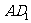 所成的角为
所成的角为 ,则
,则 的取值范围是
的取值范围是
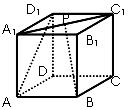
A.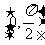 B.
B.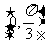 C.
C.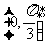 D.
D.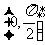
3.设函数 的反函数
的反函数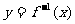 的定义域为
的定义域为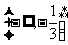 ,则
,则 的定义域D为
的定义域D为
A.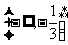 B.
B.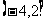 C.
C.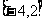 D.
D.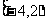
2.若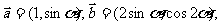 且
且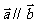 ,则
,则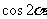 的值为
的值为
A.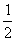 B.
B.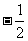 C.
C.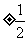 D.0
D.0
1.若集合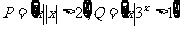 ,则
,则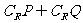 等于
等于
A. B.
B. C.
C.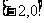 D.
D.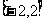
22.(本题满分14分)
已知椭圆c的中心在坐标原点,焦点在x轴上,它的一个顶点恰好是抛物线y=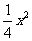 的
的
焦点,离心率为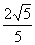
(1)求椭圆C的标准方程;
(2)过椭圆c的右焦点作直线l交椭圆c于A、B两点,交y轴于M点,若 ,求
,求 的值.
的值.
21.(本题满分12分)
我们用部分自然数构造如下的数表:用aij(i≥j)表示第i行第j个数(i、j为正整数),使ail=aii=i ;每行中的其余各数分别等于其“肩膀”上的两个数之和(第一、二行除外,如图),设第n(n为正整数)行中各数之和为bn.
(1)试写出b2一2b1;,b3-2b2,b4-2b3,b5-2b4,并推测bn+1和bn的关系(无需证明);
(2)证明数列{bn+2}是等比数列,并求数列{bn)的通项公式bn;
(3)数列{ bn}中是否存在不同的三项bp,bq,br(p,q,r为正整数)恰好成等差数
列?若存在求出P,q,r的关系;若不存在,请说明理由.
20.(本题满分12分)
设函数g(x)= (a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).
(a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).
(1)若方程f(x)=0有两个实根分别为-2和4,求f(x)的表达式;
(2)若g(x)在区间(-1,3)上是单调递减函数,求a2+b2的最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com