
1.已知一次函数y=kx+b的图象过点A(0,1)和点B(a,-3a)(a>0),且点B在反比例函数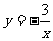 的图象上,求a及一次函数式.
的图象上,求a及一次函数式.
2.观察图象,把图象中提供、展现的信息转化为与两函数有关的知识来解题.
1.综合运用一次函数和反比例函数求解两种函数解析式,往往仍用待定系数法.
例1 已知直线y=x+b经过点A(3,0),并与双曲线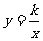 的交点为B(-2,m)和C,求k、b的值.
的交点为B(-2,m)和C,求k、b的值.
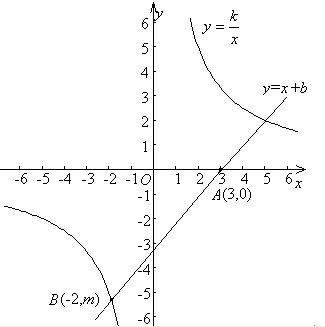
解 点A(3,0)在直线y=x+b上,所以0=3+b,b=-3.
一次函数的解析式为:y=x-3.
又因为点B(-2,m)也在直线y=x-3上,所以m=-2-3=-5,即B(-2,-5).
而点B(-2,-5)又在反比例函数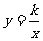 上,所以k=-2×(-5)=10.
上,所以k=-2×(-5)=10.
例2 已知反比例函数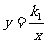 的图象与一次函数y=k2x-1的图象交于A(2,1).
的图象与一次函数y=k2x-1的图象交于A(2,1).
(1)分别求出这两个函数的解析式;
(2)试判断A点关于坐标原点的对称点与两个函数图象的关系.
分析 (1)因为点A在反比例函数和一次函数的图象上,把A点的坐标代入这两个解析式即可求出k1、k2的值.
(2)把点A关于坐标原点的对称点A′坐标代入一次函数和反比例函数解析式中,可知A′是否在这两个函数图象上.
解 (1)因为点A(2,1)在反比例函数和一次函数的图象上,所以k1=2×1=2.
1=2 k2-1,k2=1.
所以反比例函数的解析式为: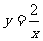 ;一次函数解析式为:y=x-1.
;一次函数解析式为:y=x-1.
(2)点A(2,1)关于坐标原点的对称点是A′(-2,-1).
把A点的横坐标代入反比例函数解析式得,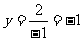 ,所以点A在反比例函数图象上.
,所以点A在反比例函数图象上.
把A点的横坐标代入一次函数解析式得,y=-2-1=-3,所以点A不在一次函数图象上.
例3 已知一次函数y=kx+b的图象经过点A(0,1)和点B(a,-3a),a<0,且点B在反比例函数的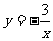 的图象上.
的图象上.
(1)求a的值.
(2)求一次函数的解析式,并画出它的图象.
(3)利用画出的图象,求当这个一次函数y的值在-1≤y≤3范围内时,相应的x的取值范围.
(4)如果P(m,y1)、Q(m+1,y2)是这个一次函数图象上的两点,试比较y1与y2的大小.
分析 (1)由于点A、点B在一次函数图象上,点B在反比例函数图象上,把这些点的坐标代入相应的函数解析式中,可求出k、b和a的值.
(2)由(1)求出的k、b、a的值,求出函数的解析式,通过列表、描点、连线画出函数图象.
(3)和(4)都是利用函数的图象进行解题.
解 (1)反比例函数的图象过点B(a,-3a),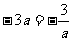 ,a=±1,因为a<0, 所以a=-1. a<0. B(-1,3).
,a=±1,因为a<0, 所以a=-1. a<0. B(-1,3).
又因为一次函数图象过点A(0,1)和点B(-1,3).
所以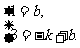 解得,
解得,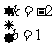 .
.
即:一次函数的解析式为y=-2x+1.
(2)


一次函数和反比例函数的图象为:
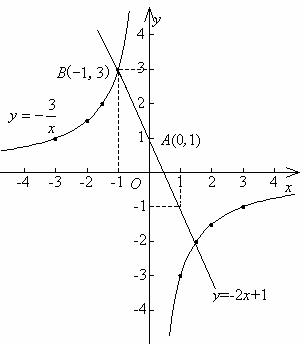
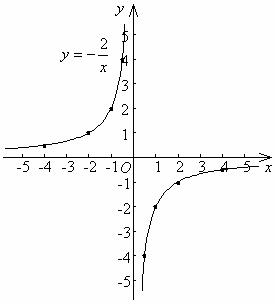
(3)从图象上可知,当一次函数y的值在-1范围内时,相应的x的值为:
-1≤x≤1.
(4)从图象可知,y随x的增大而减小,又m+1>m,所以y1>y2。
或解:当x1=m时,y1=-2m+1;当x2=m+1时,y2=-2×(m+1)+1=-2m-1
所以y1-y2=(-2m+1)-(-2m-1)=2>0,即y1> y2。
例4 如图,一次函数y=kx+b的图象与反比例函数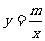 的图象交于A、B两点.
的图象交于A、B两点.
(1)利用图象中的条件,求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数值的x的取值范围.
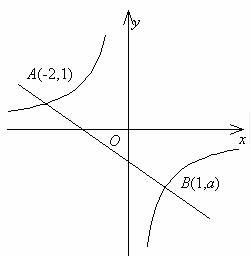
分析 (1)把A、B两点坐标代入两解析式,即可求得一次函数和反比例函数解析式 .
(2)因为图象上每一点的纵坐标与函数值是相对应的,一次函数值大于反比例函数值,反映在图象上,自变量取相同的值时,一次函数图象上点的纵坐标大于反比例函数图象上点的纵坐标.
解 (1)观察图象可知,反比例函数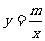 的图象过点A(-2,1),m=-2×1=-2.
的图象过点A(-2,1),m=-2×1=-2.
所以反比例函数的解析式为: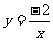 .又点B(1,a)也在反比例函数图象上,
.又点B(1,a)也在反比例函数图象上,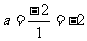 .即B(1,-2).
.即B(1,-2).
因为一次函数图象过点A、B.所以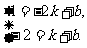 解得,
解得,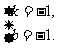
一次函数解析式为:y=-x-1.
(2)观察图象可知,当x<-2或0<x<1时,一次函数的值大于反比例函数值.
综合运用一次函数和反比例函数的知识解题,一般先根据题意画出图象,借助图象和题目中提供的信息解题.
已知正比例函数y=ax和反比例函数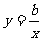 的图象相交于点(1,2),求两函数解析式.
的图象相交于点(1,2),求两函数解析式.
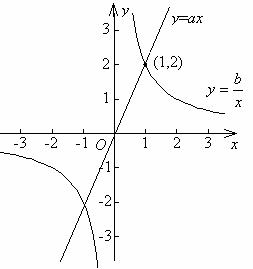
分析 根据题意可作出图象.点(1,2)在正比例函数和反比例函数图象上,把点(1,2)代入正比例函数和反比例函数的解析式中,求出a和b.
解 因为点(1,2)在正比例函数和反比例函数图象上,
把x=1,y=2分别代入y=ax和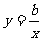 中,得
中,得
2=a,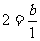 ,b=2.
,b=2.
所以正比例函数解析式为y=2x.
反比例函数解析式为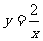 .
.
4.已知反比例函数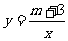 经过点A(2,-m)和B(n,2n),求:
经过点A(2,-m)和B(n,2n),求:
(1)m和n的值;
(2)若图象上有两点P1(x1,y1)和P2(x2,y2),且x1<0< x2,试比较y1和 y2的大小.
3.若反比例函数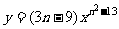 的图象在所在象限内,y随x的增大而增大,求n的值.
的图象在所在象限内,y随x的增大而增大,求n的值.
2.已知y是x的反比例函数,且当x=3时,y=8,求:
(1)y和x的函数关系式;
(2)当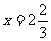 时,y的值;
时,y的值;
(3)当x取何值时,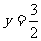 ?
?
1.在同一直角坐标系中画出下列函数的图象:
(1)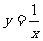 ; (2)
; (2)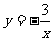 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com