
20.(本小题满分14分)
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由
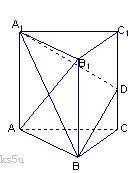 B沿棱柱侧面经过棱C C1到点A1的最短路线长为
B沿棱柱侧面经过棱C C1到点A1的最短路线长为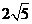 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交
点为D.
(1)求三棱柱ABC-A1B1C1的体积;
(2)在平面A1BD内是否存在过点D的直线与平面ABC平行?证明你的判断;
(3)证明:平面A1BD⊥平面A1ABB1.
19.(本小题满分14分)
已知函数f(x)的定义域为R,对任意的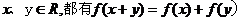 ,且当
,且当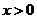 时,
时,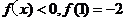 .
.
(Ⅰ)求证:函数f(x)为奇函数;
(Ⅱ)求证: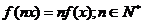
(Ⅲ)求函数 在区间[-n,n](n
在区间[-n,n](n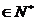 )上的最大值和最小值。
)上的最大值和最小值。
18.(本小题满分14分)
在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点,已知|AB|=2|OA|,且点B的纵坐标大于0。
(Ⅰ)求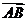 的坐标;
的坐标;
(Ⅱ)求圆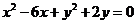 关于直线OB对称的圆的方程。
关于直线OB对称的圆的方程。
17.(本小题满分12分)
某次有奖竞猜活动中,主持人准备了A、B两个相互独立的问题, 并且宣布:观众答对问题A可获奖金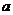 元,答对问题B可获奖金2
元,答对问题B可获奖金2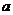 元;先答哪个题由观众自由选择;只有第一个问题答对,才能再答第二个问题,否则终止答题.设某幸运观众答对问题A、B的概率分别为
元;先答哪个题由观众自由选择;只有第一个问题答对,才能再答第二个问题,否则终止答题.设某幸运观众答对问题A、B的概率分别为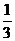 、
、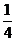 .你觉得他应先回答哪个问题才能使获得奖金的期望较大?说明理由.
.你觉得他应先回答哪个问题才能使获得奖金的期望较大?说明理由.
16.(本小题满分12分)
已知:复数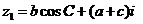 ,
,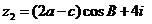 ,且
,且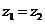 ,其中
,其中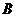 、
、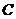 为△ABC的内角,
为△ABC的内角,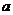 、
、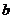 、
、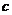 为角
为角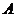 、
、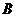 、
、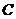 所对的边.
所对的边.
(Ⅰ)求角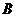 的大小;
的大小;
(Ⅱ) 若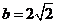 ,求△ABC的面积.
,求△ABC的面积.
15.(几何证明选讲选做题) 如图:PA与圆O相切于A,PCB为圆O的割线,
并且不过圆心O,已知∠BPA=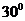 , PA=
, PA=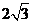 ,PC=1,
,PC=1,
则圆O的半径等于 .
14、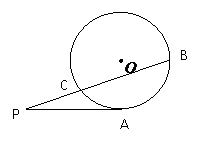 (坐标系与参数方程选做题) 极坐标系中,曲线
(坐标系与参数方程选做题) 极坐标系中,曲线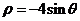 和
和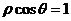 相交于点
相交于点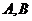 ,则
,则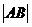 =
;
=
;
13、椭圆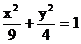 的焦点为
的焦点为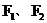 ,点P为其上的动点,当
,点P为其上的动点,当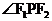 为钝角时,点P横坐标的取值范围是_______________________;
为钝角时,点P横坐标的取值范围是_______________________;
12、若函数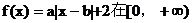 上为增函数,则实数a、b的取值范围是___________;
上为增函数,则实数a、b的取值范围是___________;
11、已知集合为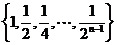 ,它的所有的三个元素的子集的和是
,它的所有的三个元素的子集的和是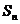 ,则
,则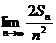 =
。
=
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com